Giải SGK Toán 10 Bài 1 (Chân trời sáng tạo): Giá trị lượng giác của một góc từ 0 đến 180

Giải bài tập Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180

Video bài giảng Giá trị lượng giác của một góc từ 0 đến 180 – Chân trời sáng tạo

1. Giá trị lượng giác

Giải toán lớp 10 trang 61 Tập 1 Chân trời sáng tạo

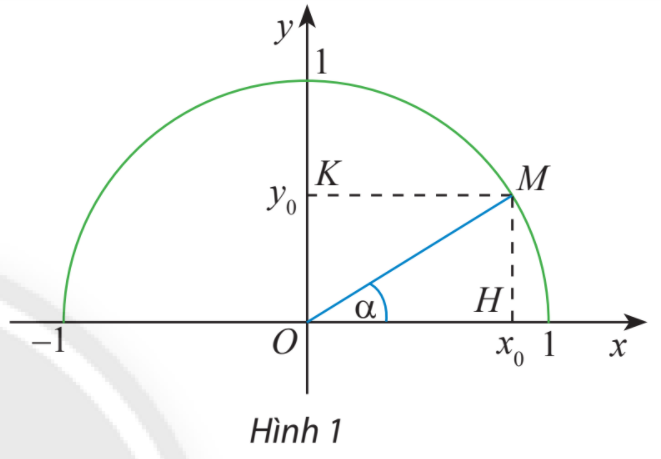
HĐ Khám phá 1 trang 61 Toán lớp 10: Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính $R=1$ nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn $\alpha ,$lấy điểm M trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha .$ Giả sử điểm M có tọa độ $(x_0;y_0).$ Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:

 $\sin \alpha =y_0;\cos \alpha =x_0;\tan \alpha =\frac{y_0}{x_0};\cot \alpha =\frac{x_0}{y_0}.$

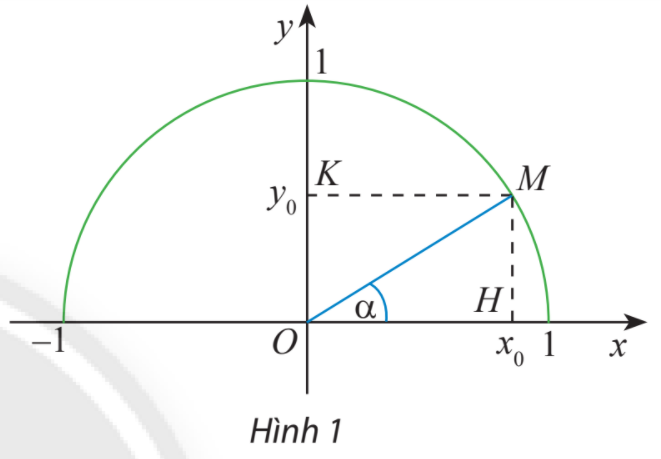
Phương pháp giải:

Tam giác vuông OHM có $\alpha =\widehat{xOM}$

$\sin \alpha =\frac{MH}{OM};\cos \alpha =\frac{OH}{OM};\tan \alpha =\frac{\sin \alpha }{\cos \alpha };\cot \alpha =\frac{\cos \alpha }{\sin \alpha }.$

Lời giải:

Ta có: tam giác vuông OHM vuông tại H và $\alpha =\widehat{xOM}$

Do đó: $\sin \alpha =\frac{MH}{OM};\cos \alpha =\frac{OH}{OM}.$

Mà $MH=y_0;OH=x_0;OM=1.$

$\Rightarrow \sin \alpha =\frac{y_0}{1}=y_0;\cos \alpha =\frac{x_0}{1}=x_0.$

$\Rightarrow \tan \alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{y_0}{x_0};\cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{x_0}{y_0}.$

Giải toán lớp 10 trang 62 Tập 1 Chân trời sáng tạo

Thực hành 1 trang 62 Toán lớp 10: Tìm các giá trị lượng giác của góc ${135}^o$

Phương pháp giải:

Gọi M là điểm trên nửa đường tròn đơn vị sao cho $\widehat{xOM}={135}^o$

Khi đó hoành độ và tung độ của điểm M lần lượt là các giá trị $\cos {135}^o,\sin {135}^o$

Từ đó suy ra$\tan {135}^o=\frac{\sin {135}^o}{\cos {135}^o},\cot {135}^o=\frac{\cos {135}^o}{\sin {135}^o}.$

Lời giải:

Lấy điểm M trên nửa đường tròn đơn vị sao cho $\widehat{xOM}={135}^o$, H là hình chiếu vuông góc của M trên Oy.

 

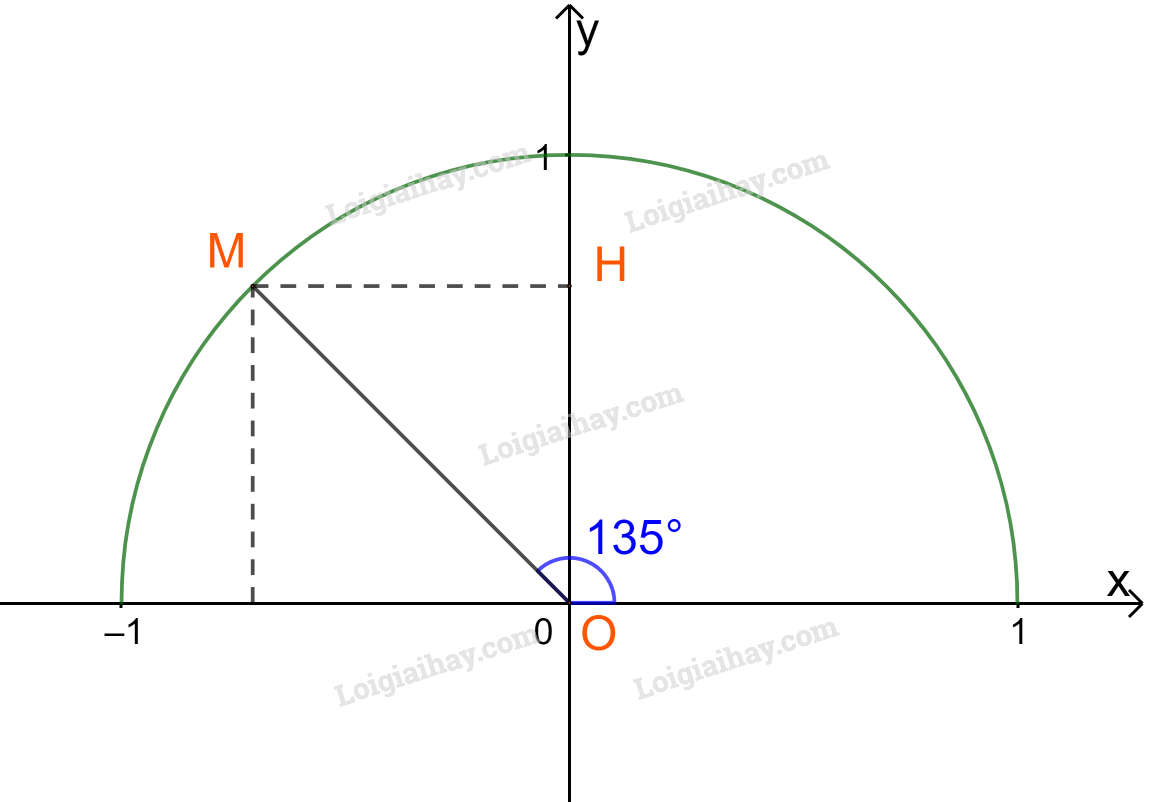
Ta có: $\widehat{MOy}={135}^o-{90}^o={45}^o$.

Tam giác OMH vuông cân tại H nên $OH=MH=\frac{OM}{\sqrt{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}.$

Vậy tọa độ điểm M là $\left(-\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2}\right).$

Vậy theo định nghĩa ta có:

 $\begin{array}{l}\sin {135}^o=\frac{\sqrt{2}}{2};\cos {135}^o=-\frac{\sqrt{2}}{2};\\ \tan {135}^o=-1;\cot {135}^o=-1.\end{array}$

Chú ý

Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc ${135}^o$

Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:

Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)

Tính $\sin {135}^o$, bấm phím:  sin  1  3  5  ${}^o$’’’  = ta được kết quả là $\frac{\sqrt{2}}{2}$

Tính $\cos {135}^o$,bấm phím:  cos  1  3  5  ${}^o$’’’  = ta được kết quả là $\frac{-\sqrt{2}}{2}$

Tính $\tan {135}^o$, bấm phím:  tan  1  3  5  ${}^o$’’’  = ta được kết quả là $-1$

(Để tính $\cot {135}^o$, ta tính $1:\tan {135}^o$)

2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau

HĐ Khám phá 2 trang 62 Toán lớp 10: Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc $\widehat{xOM}$ và $\widehat{xON}.$

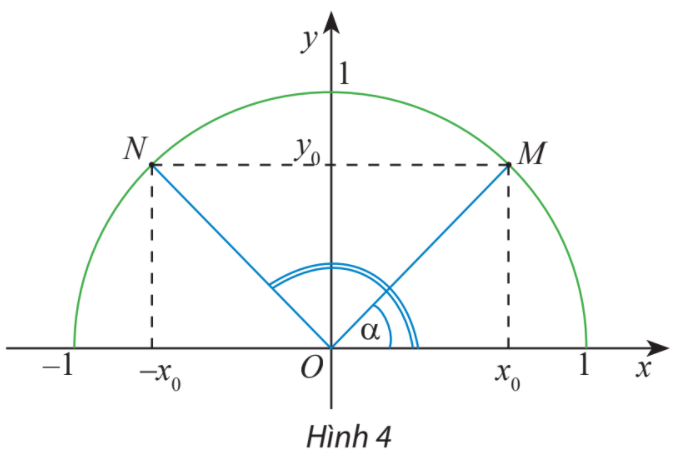
Phương pháp giải:

Tính góc $\widehat{xON}$ theo góc $\widehat{xOM}.$

Lời giải:

Gọi H là hình chiếu vuông góc của N Ox.

 

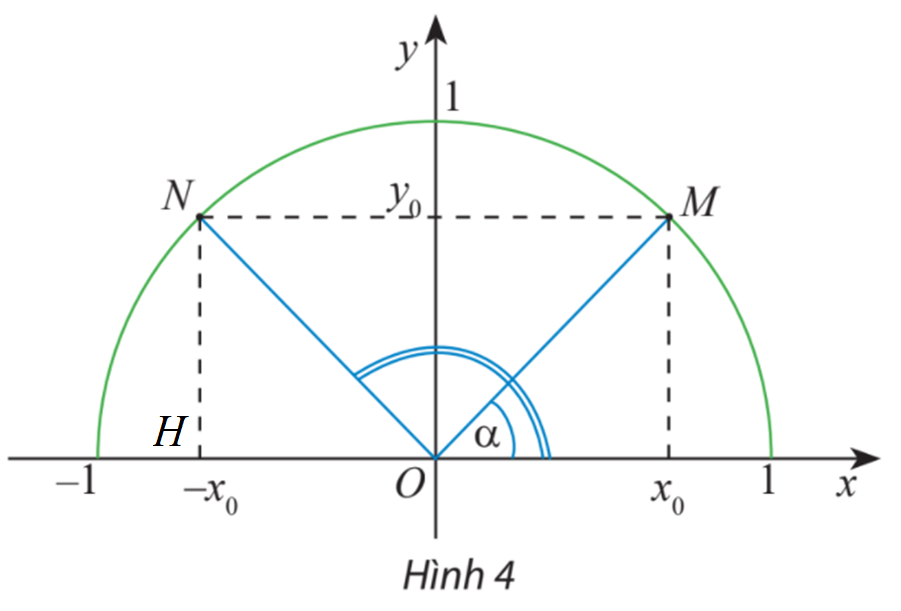
Ta có: $\widehat{NOH}=\widehat{ONM}=\widehat{OMN}=\widehat{MOx}=\alpha$ (do NM song song với Ox)

Mà $\widehat{xOM}+\widehat{NOH}={180}^o$

Suy ra $\widehat{xON}+\widehat{MOx}={180}^o$

Giải toán lớp 10 trang 63 Tập 1 Chân trời sáng tạo

Thực hành 2 trang 63 Toán lớp 10: Tính các giá trị lượng giác: $\sin {120}^o;\cos {150}^o;\cot {135}^o.$

Phương pháp giải:

$\begin{array}{l}\sin {120}^o=\sin ({180}^o-{60}^o);\\ \cos {150}^o=-\cos ({180}^o-{30}^o);\\ \cot {135}^o=-\cot ({180}^o-{45}^o).\end{array}$

Lời giải: 

$\begin{array}{l}\sin {120}^o=\sin ({180}^o-{60}^o)=\sin {60}^o=\frac{\sqrt{3}}{2};\\ \cos {150}^o=-\cos ({180}^o-{30}^o)=-\cos {30}^o=-\frac{\sqrt{3}}{2};\\ \cot {135}^o=-\cot ({180}^o-{45}^o)=-\cot {45}^o=-1.\end{array}$

Vận dụng 1 trang 63 Toán lớp 10: Cho biết $\sin \alpha =\frac{1}{2},$ tìm góc $\alpha (0^o\le \alpha \le {180}^o)$ bằng cách vẽ nửa đường tròn đơn vị.

Phương pháp giải:

Vẽ nửa đường tròn đơn vị.

$\sin \alpha =\frac{1}{2}$ nên lấy các điểm có tung độ là $\frac{1}{2}$. Từ đó tính góc $\alpha$.

Lời giải:

Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho: $\widehat{xOM}=\alpha$

Do $\sin \alpha =\frac{1}{2}$ nên tung độ của M bằng $\frac{1}{2}.$

Vậy ta xác định được hai điểm N và M thỏa mãn $\sin \widehat{xON}=\sin \widehat{xOM}=\frac{1}{2}$

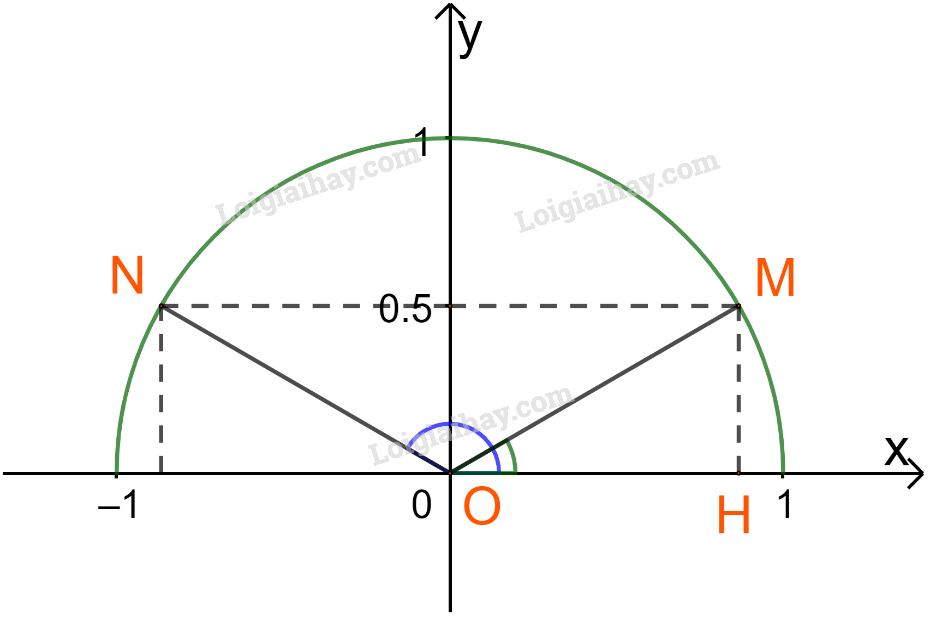
Đặt $\beta =\widehat{xOM}\Rightarrow \widehat{xON}={180}^o-\beta$

Xét tam giác OHM vuông tại H ta có: $MH=\frac{1}{2}=\frac{OM}{2}\Rightarrow \beta ={30}^o$

$\Rightarrow \widehat{xON}={180}^o-{30}^o={150}^o$

Vậy $\alpha ={30}^o$ hoặc $\alpha ={150}^o$

3. Giá trị lượng giác của một số góc đặc biệt

Thực hành 3 trang 63 Toán lớp 10: Tính:

$A=\sin {150}^o+\tan {135}^o+\cot {45}^o$

$B=2\cos {30}^o-3\tan 150+\cot {135}^o$

Phương pháp giải:

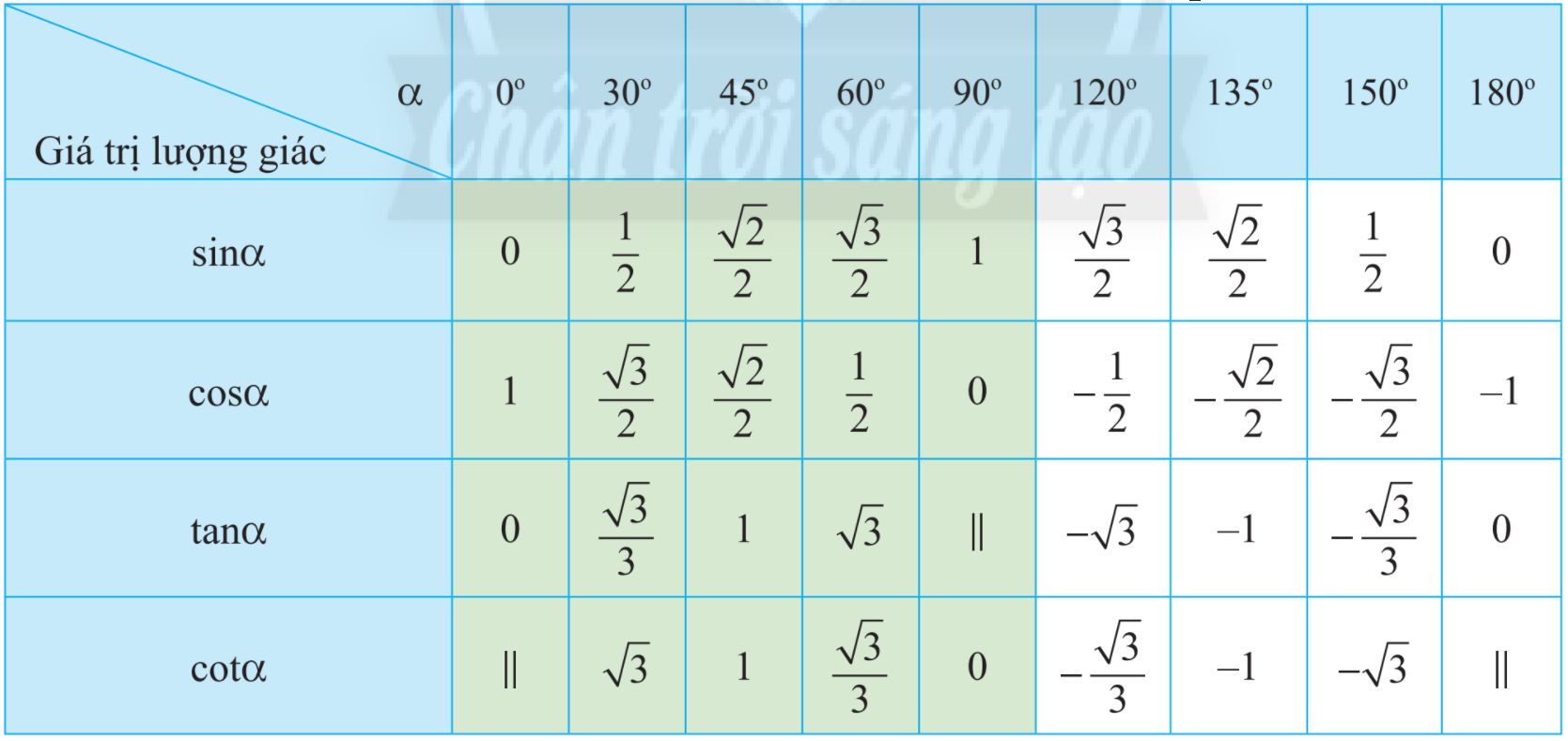
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt.

Lời giải:

$A=\sin {150}^o+\tan {135}^o+\cot {45}^o$

Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:

$\sin {150}^o=\frac{1}{2};\tan {135}^o=-1;\cot {45}^o=1.$

$\Rightarrow A=\frac{1}{2}-1+1=\frac{1}{2}.$

$B=2\cos {30}^o-3\tan 150+\cot {135}^o$

Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:

$\cos {30}^o=\frac{\sqrt{3}}{2};\tan {150}^o=-\frac{\sqrt{3}}{3};\cot {135}^o=-1.$

$\Rightarrow B=2.\frac{\sqrt{3}}{2}-3.\left(-\frac{\sqrt{3}}{3}\right)+1=5\sqrt{3}+1.$

Giải toán lớp 10 trang 64 Tập 1 Chân trời sáng tạo

Vận dụng 2 trang 64 Toán lớp 10: Tìm góc $\alpha (0^o\le \alpha \le {180}^o)$ trong mỗi trường hợp sau:

a) $\sin \alpha =\frac{\sqrt{3}}{2}$

b) $\cos \alpha =\frac{-\sqrt{2}}{2}$

c) $\tan \alpha =-1$

d) $\cot \alpha =-\sqrt{3}$

Phương pháp giải:

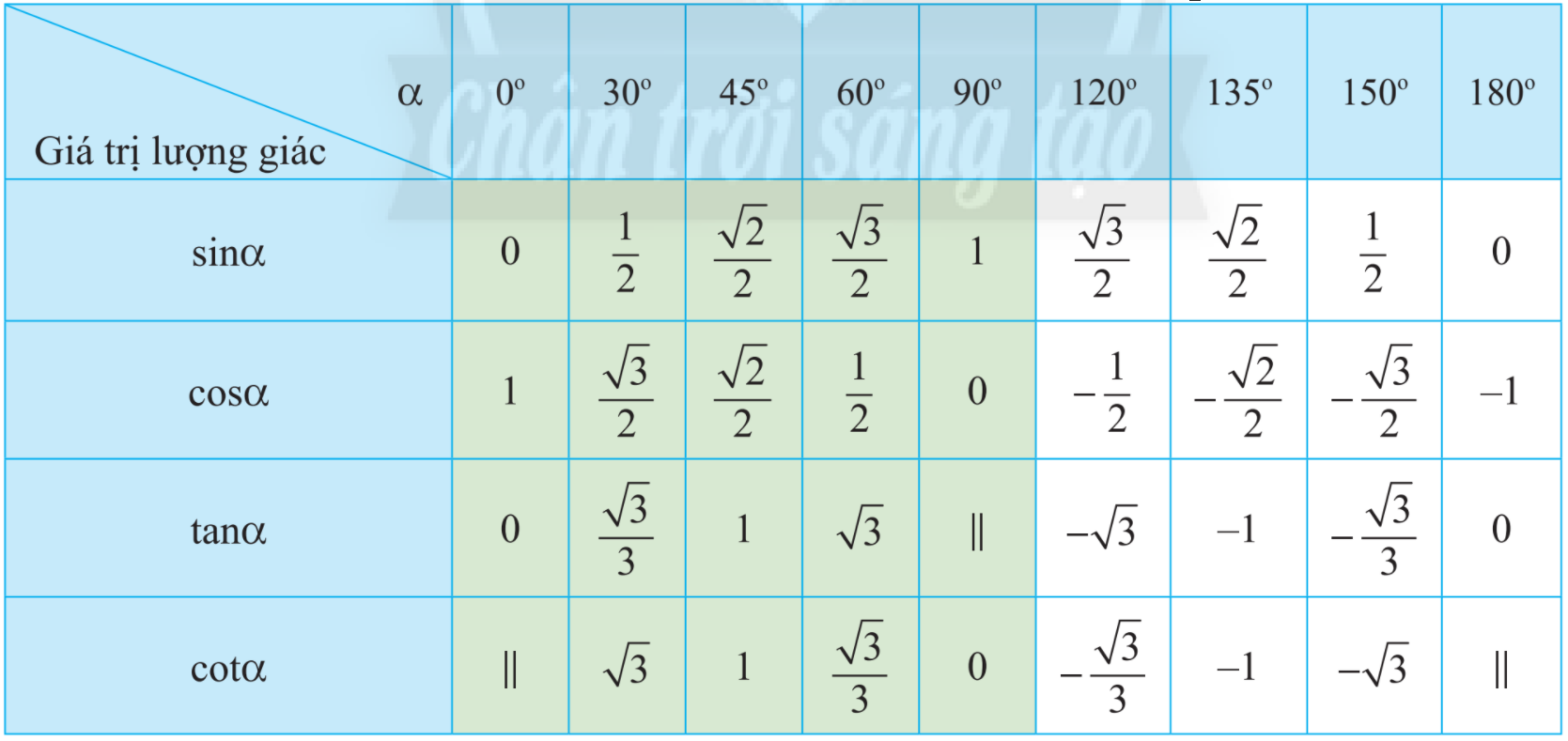
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt để tìm góc.

Lời giải:

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\sin \alpha$ ta có:

$\sin \alpha =\frac{\sqrt{3}}{2}$ với $\alpha ={60}^o$ và $\alpha ={120}^o$

b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cos \alpha$ ta có:

$\cos \alpha =\frac{-\sqrt{2}}{2}$ với $\alpha ={135}^o$

c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\tan \alpha$ ta có:

$\tan \alpha =-1$ với $\alpha ={135}^o$

d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cot \alpha$ ta có:

$\cot \alpha =-\sqrt{3}$ với $\alpha ={150}^o$

4. Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc

Giải toán lớp 10 trang 65 Tập 1 Chân trời sáng tạo

Thực hành 4 trang 65 Toán lớp 10: a) Tính $\cos 80°43‘51‘‘$; $\tan 147°12‘25‘‘$; $cot 99°9‘19‘‘$

b) Tìm $\alpha (0°\le \alpha \le 180°)$, biết $\cos \alpha =–0,723$ 

Phương pháp giải:

a) Sử dụng máy tính cầm tay, bấm liên tiếp các phím:

 

Để tính $\cot {99}^o{9}^{\prime }{19}^{″}$ ta tính $1:\tan {99}^o{9}^{\prime }{19}^{″}$.

b) Sử dụng máy tính cầm tay, bấm liên tiếp các phím:

 

Lời giải:

a)

$\begin{array}{l}\cos {80}^o{43}^{\prime }{51}^{″}=0,161;\\ \tan {147}^o{12}^{\prime }{25}^{″}=-0,644;\\ \cot {99}^o{9}^{\prime }{19}^{″}=-0,161\end{array}$

b) $\alpha ={136}^o{18}^{\prime }9,{81}^{″}.$

Bài tập

Bài 1 trang 65 Toán lớp 10: Cho biết sin 30° = $\frac{1}{2}$; sin60° = $\frac{\sqrt{3}}{2}$ ; tan45° = 1. Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của E = 2cos30° + sin150° + tan135°.

Phương pháp giải:

$\begin{array}{l}\cos {30}^o=\sin \left({90}^o-{30}^o\right)=\sin {60}^o\\ \sin {150}^o=\sin \left({180}^o-{150}^o\right)=\sin {30}^o\\ \tan {135}^o=-\tan \left({180}^o-{135}^o\right)=-\tan {45}^o\end{array}$

Lời giải:

Ta có:

$\begin{array}{l}\cos {30}^o=\sin \left({90}^o-{30}^o\right)=\sin {60}^o=\frac{\sqrt{3}}{2};\\ \sin {150}^o=\sin \left({180}^o-{150}^o\right)=\sin {30}^o=\frac{1}{2};\\ \tan {135}^o=-\tan \left({180}^o-{135}^o\right)=-\tan {45}^o=-1\end{array}$

$\Rightarrow E=2.\frac{\sqrt{3}}{2}+\frac{1}{2}-1=\sqrt{3}-\frac{1}{2}.$

Bài 2 trang 65 Toán lớp 10: Chứng minh rằng:

a) sin20° = sin160°;

b) cos50° =  – cos130°.

Phương pháp giải:

$\begin{array}{l}\sin \left({180}^o-\alpha \right)=\sin \alpha \\ \cos \left({180}^o-\alpha \right)=-\cos \alpha \end{array}$$(0^o\le \alpha \le {180}^o)$

Lời giải:

a) $\sin {20}^o=\sin \left({180}^o-{160}^o\right)=\sin {160}^o$

b) $\cos {50}^o=\cos ({180}^o-{130}^o)=-\cos {130}^o$

Bài 3 trang 65 Toán lớp 10: Tìm α (0° ≤ α  ≤ 180°) trong mỗi trường hợp sau:

a) cosα  = $\frac{-\sqrt{2}}{2}$ ;

b) sinα  = 0;

c) tanα  = 1;

d) cotα  không xác định.

Phương pháp giải:

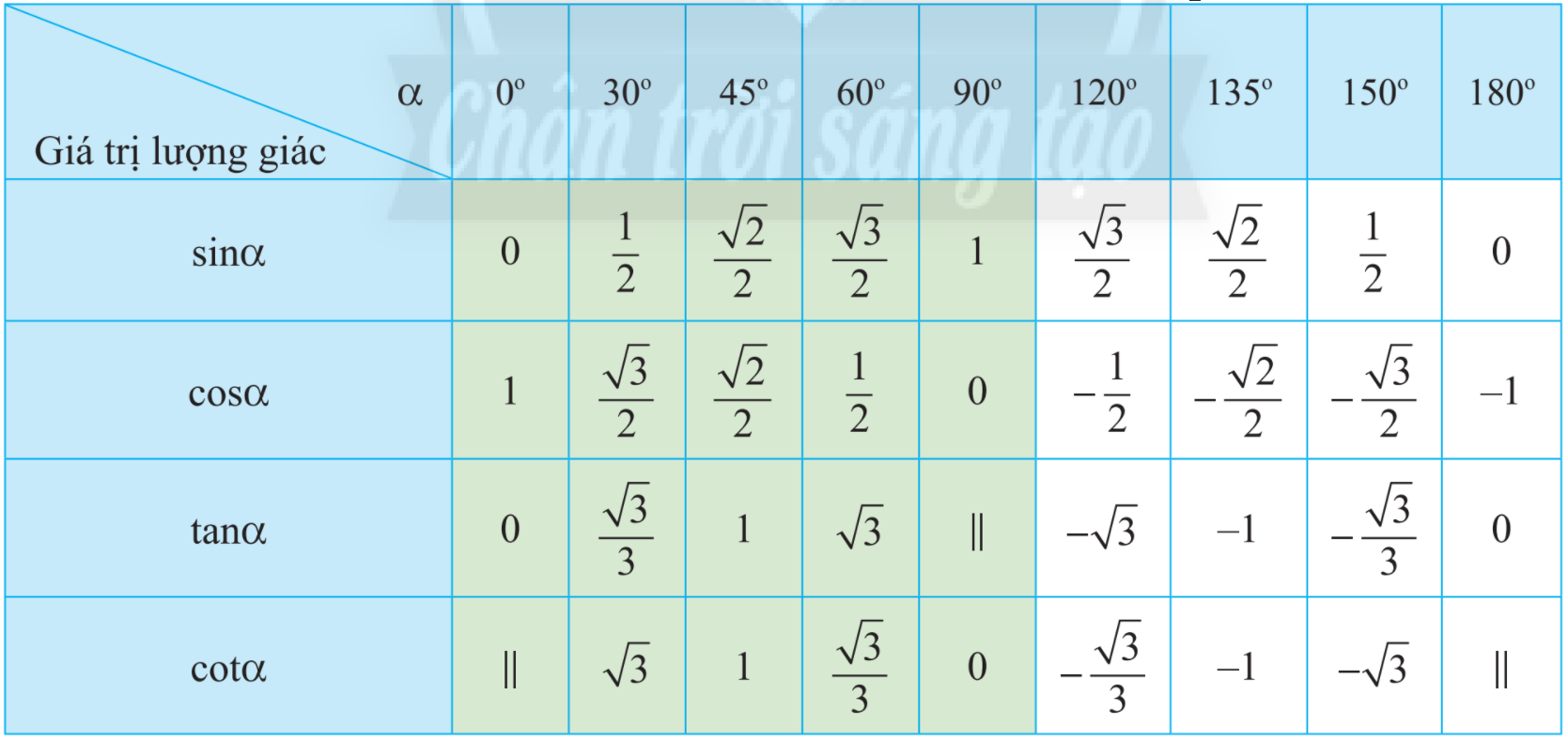
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt để tìm góc.

Lời giải:

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cos \alpha$ ta có:

$\cos \alpha =\frac{-\sqrt{2}}{2}$ với $\alpha ={135}^o$

b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\sin \alpha$ ta có:

$\sin \alpha =0$ với $\alpha =0^o$ và $\alpha ={180}^o$

c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\tan \alpha$ ta có:

$\tan \alpha =1$ với $\alpha ={45}^o$

d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cot \alpha$ ta có:

$\cot \alpha$ không xác định với $\alpha =0^o$

Bài 4 trang 65 Toán lớp 10: Cho tam giác ABC. Chứng minh rằng:

a) sinA = sin(B + C);

b) cosA =  – cos(B + C).

Phương pháp giải:

$\begin{array}{l}\sin \left({180}^o-A\right)=\sin A\\ \cos \left({180}^o-A\right)=-\cos A\end{array}$$(0^o\le \hat{A}\le {180}^o)$

Lời giải: 

a)

$\sin (B+C)=\sin \left({180}^o-A\right)=\sin A$

Vậy $\sin A=\sin (B+C)$

b)

$\cos (B+C)=\cos \left({180}^o-A\right)=-\cos A$

Vậy $\cos A=-\cos (B+C)$

Bài 5 trang 65 Toán lớp 10: Chứng minh rằng với mọi góc α (0° ≤ α  ≤ 180°), ta đều có:

a) cos2α  + sin2α  = 1;

b) tanα  . cotα  = 1 (0° < α  < 180°, α  ≠ 90°).

c) 1 + tan2α  = $\frac{1}{{\cos }^2\alpha }$ (α  ≠ 90°);

d) 1 + cot2 α  = $\frac{1}{{\sin }^2\alpha }$ (0° < α  < 180°).

Lời giải:

a) ${\cos }^2\alpha +{\sin }^2\alpha =1$

Trên nửa đường tròn đơn vị, lấy điểm M sao cho $\widehat{xOM}=\alpha$

Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.

 

Ta có: tam giác vuông OHM vuông tại H và $\alpha =\widehat{xOM}$

Do đó: $\sin \alpha =\frac{MH}{OM}=MH;\cos \alpha =\frac{OH}{OM}=OH.$

$\Rightarrow {\cos }^2\alpha +{\sin }^2\alpha =O{H}^2+M{H}^2=O{M}^2=1$

b) $\tan \alpha .\cot \alpha =1(0^o<\alpha <{180}^o,\alpha \ne {90}^o)$

Ta có:

$\begin{array}{l}\tan \alpha =\frac{\sin \alpha }{\cos \alpha };\cot \alpha =\frac{\cos \alpha }{\sin \alpha }.\\ \Rightarrow \tan \alpha .\cot \alpha =\frac{\sin \alpha }{\cos \alpha }.\frac{\cos \alpha }{\sin \alpha }=1\end{array}$

c) $1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }(\alpha \ne {90}^o)$

Với $\alpha \ne {90}^o$ ta có:

$\begin{array}{l}\tan \alpha =\frac{\sin \alpha }{\cos \alpha };\\ \Rightarrow 1+{\tan }^2\alpha =1+\frac{{\sin }^2\alpha }{{\cos }^2\alpha }=\frac{{\sin }^2\alpha +{\cos }^2\alpha }{{\cos }^2\alpha }=\frac{1}{{\cos }^2\alpha }\end{array}$

d) $1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }(0^o<\alpha <{180}^o)$

Ta có:

$\begin{array}{l}\cot \alpha =\frac{\cos \alpha }{\sin \alpha };\\ \Rightarrow 1+{\cot }^2\alpha =1+\frac{{\cos }^2\alpha }{{\sin }^2\alpha }=\frac{{\sin }^2\alpha +{\cos }^2\alpha }{{\sin }^2\alpha }=\frac{1}{{\sin }^2\alpha }\end{array}$

Bài 6 trang 65 Toán lớp 10: Cho góc α với cosα  = $-\frac{\sqrt{2}}{2}$ . Tính giá trị của biểu thức A = 2sin2α  + 5cos2α .

Phương pháp giải:

Sử dụng đẳng thức ${\cos }^2\alpha +{\sin }^2\alpha =1$

Lời giải:

Ta có: $A=2{\sin }^2\alpha +5{\cos }^2\alpha =2({\sin }^2\alpha +{\cos }^2\alpha )+3{\cos }^2\alpha$

Mà ${\cos }^2\alpha +{\sin }^2\alpha =1;\cos \alpha =-\frac{\sqrt{2}}{2}.$

$\Rightarrow A=2+3.{\left(-\frac{\sqrt{2}}{2}\right)}^2=2+3.\frac{1}{2}=\frac{7}{2}.$

Bài 7 trang 65 Toán lớp 10: Dùng máy tính cầm tay, hãy thực hiện các yêu cầu dưới đây:

a) Tính: sin168°45’33”; cos17°22’35”; tan156°26’39”; cot 56°36’42”.

b) Tìm α (0° ≤ α  ≤ 180°) trong các trường hợp sau:

i) sinα  = 0,862;

ii) cosα  =  – 0,567;

iii) tanα  = 0,334.

Phương pháp giải:

a) Để tính $\sin {168}^o{45}^{\prime }{33}^{″}$, bấm liên tiếp các phím:

Để tính $\cot {56}^o{36}^{\prime }{42}^{″}$ ta tính $1:\tan {56}^o{36}^{\prime }{42}^{″}$.

b) Để tìm $\alpha$ biết $\sin \alpha =0,862$, bấm liên tiếp các phím:

Lời giải: 

a)

$\begin{array}{l}\sin {168}^o{45}^{\prime }{33}^{″}=0,195;\\ \cos {17}^o{22}^{\prime }{35}^{″}=0,954;\\ \tan {156}^o{26}^{\prime }{39}^{″}=-0,436;\\ \cot {56}^o{36}^{\prime }{42}^{″}=0,659\end{array}$

b)

i) $\alpha ={59}^o{32}^{\prime }30,8^{″}.$

ii) $\alpha ={124}^o{32}^{\prime }28,{65}^{″}.$

iii) $\alpha ={18}^o{28}^{\prime }9,{55}^{″}.$

Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 3

Bài 2: Định lí cosin và định lí sin

Bài 3: Giải tam giác và ứng dụng thực tế

Bài tập cuối chương 4