35 câu Trắc nghiệm Chương 3: Hàm số bậc hai và đồ thị (Chân trời sáng tạo 2023) có đáp án – Toán lớp 10

Trắc nghiệm Toán 10 Chương 3: Hàm số bậc hai và đồ thị

I. Nhận biết

Câu 1. Trong các hàm số sau đây, hàm số nào là hàm số bậc hai?

A. y = 2x³ + 3x² – x + 5;       

B. y = 2x – 1;

C. y = –10;

D. y = x² + 7x + 10.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Hàm số bậc hai có dạng y = ax² + bx + c (với a ≠ 0).

Ta thấy hàm số ở đáp án D có dạng như trên nên hàm số ở đáp án D là hàm số bậc hai.

Vậy ta chọn đáp án D.

Câu 2. Cho hàm số y = –x² + 5x – 4. Khẳng định nào sau đây đúng?

A. Hàm số đạt giá trị lớn nhất bằng $\frac{5}{2}$ ; 

B. Hàm số đạt giá trị nhỏ nhất bằng $\frac{5}{2}$ ;        

C. Hàm số đạt giá trị nhỏ nhất bằng $\frac{9}{4}$;      

D. Hàm số đạt giá trị lớn nhất bằng $\frac{9}{4}$ .

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Hàm số đã cho có dạng y = ax² + bx + c, với a = –1, b = 5, c = –4.

∆ = b² – 4ac = 52 – 4.(–1).(–4) = 9.

Vì a = –1 < 0 nên hàm số đạt giá trị lớn nhất bằng $\frac{-\Delta }{4a}=\frac{-9}{4.\left(-1\right)}=\frac{9}{4}$ tại $x=\frac{-b}{2a}=\frac{-5}{2.\left(-1\right)}=\frac{5}{2}$

Vậy hàm số đạt giá trị lớn nhất bằng $\frac{9}{4}$ tại x = $\frac{5}{2}$

Ta chọn phương án D.

Câu 3. Cho hàm số y = f(x) = x² + 3x + 4. Bảng giá trị của hàm số đã cho là:

A.

x	–3	–2	$–\frac{3}{2}$	–1	0
f(x)	8	2	1	2	8

 

 

 

 

B.

x	–3	–2	$–\frac{3}{2}$	–1	0
f(x)	4	6	5	4	6

 

 

 

 

C.

x	–3	–2	$–\frac{3}{2}$	–1	0
f(x)	4	2	$\frac{7}{4}$	2	4

 

 

 

 

 

D.

x	–3	–2	$–\frac{3}{2}$	–1	0
f(x)	2	4	$\frac{7}{4}$	2	4

 

Hướng dẫn giải

Đáp án: C

Giải thích:

Xét hàm số y = f(x) = x² + 3x + 4.

• Với x = –3, ta có f(–3) = (–3)² + 3.(–3) + 4 = 4.

• Với x = –2, ta có f(–2) = (–2)² + 3.(–2) + 4 = 2.

• Với x = $-\frac{3}{2}$, ta có $f\left(-\frac{3}{2}\right)={\left(-\frac{3}{2}\right)}^2+3.\left(-\frac{3}{2}\right)+4=\frac{7}{4}$

• Với x = –1, ta có f(–1) = (–1)² + 3.(–1) + 4 = 2.

• Với x = 0, ta có f(0) = 0² + 3.0 + 4 = 4.

Vậy bảng giá trị của hàm số đã cho là:

x	–3	–2	$–\frac{3}{2}$	–1	0
f(x)	4	2	$\frac{7}{4}$	2	4

Do đó ta chọn đáp án C.

Câu 4. Cho hàm số y = f(x) = ax² + bx + c có đồ thị như hình vẽ:

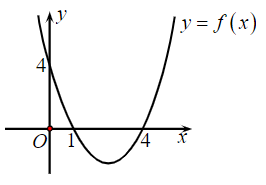
Đặt ∆ = b² – 4ac. Tìm dấu của a và ∆.

A. a > 0, ∆ > 0;

B. a < 0, ∆ > 0;

C. a > 0, ∆ = 0;

D. a < 0, ∆ = 0.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Quan sát đồ thị, ta thấy parabol có bề lõm quay lên trên nên a > 0.

Lại có đồ thị cắt trục Ox tại hai điểm phân biệt (cụ thể là tại x = 1 và x = 4) nên phương trình ax² + bx + c = 0 có hai nghiệm x₁, x₂.

Do đó ∆ > 0.

Vậy a > 0, ∆ > 0.

Do đó ta chọn phương án A.

Câu 5. Đồ thị của hàm số $y=-\frac{x}{2}+2$ là hình nào trong các hình dưới đây?

A.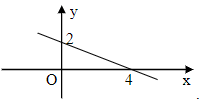 

B.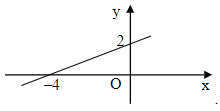 

C.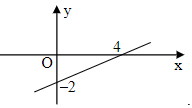 

D.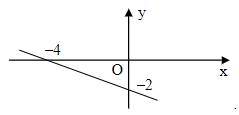 

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Ta đặt $y=f\left(x\right)=-\frac{x}{2}+2$

• Với x = 0, ta có f(0) = $-\frac{0}{2}+2=2$

Khi đó đồ thị hàm số đã cho đi qua điểm M(0; 2).

Do đó ta loại phương án C và D.

• Với y = 0, ta có f(x) = $-\frac{x}{2}+2=0$

$-\frac{x}{2}=-2$ $\Rightarrow x= 4$

Khi đó đồ thị hàm số đã cho đi qua điểm N(4; 0).

Do đó ta loại phương án B.

Vì vậy đồ thị ở phương án A là đồ thị của hàm số đã cho.

Vậy ta chọn phương án A.

Câu 6. Cho bảng dữ liệu sau đây cho biết số lượng các mặt hàng bán được trong 4 tuần vừa qua của một cửa hàng văn phòng phẩm:

Mặt hàng	Vở trắng	Bút bi	Tẩy	Bút chì	Thước
Số lượng	200	350	150	380	270

Bảng dữ liệu trên có biểu thị một hàm số không? Nếu có hãy xác định tập xác định và tập giá trị của hàm số đó.

A. Bảng dữ liệu trên biểu thị một hàm số. Tập xác định D = {200; 350; 150; 380; 270}; Tập giá trị T = {Vở trắng; Bút bi; Tẩy; Bút chì; Thước};              

B. Bảng dữ liệu trên biểu thị một hàm số. Tập xác định D = {Vở trắng; Bút bi; Tẩy; Bút chì; Thước}. Tập giá trị T = {200; 350; 150; 380; 270};              

C. Bảng dữ liệu trên biểu thị một hàm số. Tập xác định D = {Vở trắng; Bút bi; Tẩy; Bút chì; Thước}. Tập giá trị T = ∅;                

D. Bảng dữ liệu trên không biểu thị một hàm số.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Từ bảng dữ liệu đã cho, ta thấy ứng với mỗi mặt hàng trong bảng đều có một giá trị số lượng bán được duy nhất.

Vì vậy bảng trên biểu thị một hàm số.

Hàm số đó có:

+) Tập xác định D = {Vở trắng; Bút bi; Tẩy; Bút chì; Thước}.

+) Tập giá trị T = {200; 350; 150; 380; 270}.

Vậy ta chọn phương án B.

Câu 7. Tọa độ đỉnh của parabol y = –x² – 4x + 3 là:

A. S(2; 7);

B. S(–2; –7);

C. S(–2; 7);

D. S(2; –7).

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Hàm số đã cho có dạng y = ax² + bx + c, với a = –1, b = –4, c = 3.

Vì b = –4 nên ta có b’ = –2.

∆’ = b’² – ac = (–2)² – (–1).3 = 7.

Đỉnh S có tọa độ:

⦁ $x_S=-\frac{b^{‘}}{a}=-\frac{-2}{-1}=-2$

⦁ $y_S=-\frac{{\Delta }^{‘}}{a}=-\frac{7}{-1}=7$

Suy ra tọa độ đỉnh S(–2; 7).

Vậy ta chọn phương án C.

Câu 8. Biểu đồ sau đây cho biết tốc độ tăng GDP các năm của Việt Nam giai đoạn 2016 – 2020 (Nguồn: Báo Lao động):

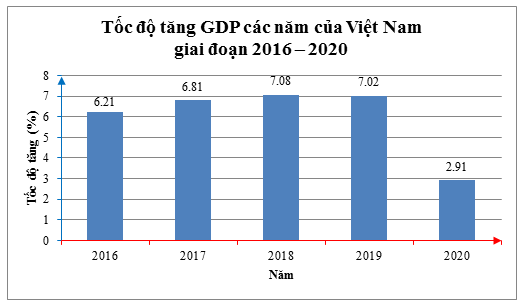
Biểu đồ trên có biểu thị cho ta một hàm số không? Nếu có hãy xác định tập xác định và tập giá trị của hàm số đó.

A. Biểu đồ trên biểu thị một hàm số. Tập xác định D = {2016; 2017; 2018; 2019; 2020}. Tập giá trị T = {6,21; 6,81; 7,08; 7,02; 2,91};

B. Biểu đồ trên biểu thị một hàm số. Tập xác định D = {6,21; 6,81; 7,08; 7,02; 2,91}. Tập giá trị T = {2016; 2017; 2018; 2019; 2020};            

C. Biểu đồ trên biểu thị một hàm số. Tập xác định T = {2016; 2017; 2018; 2019; 2020}. Tập giá trị D = {6,21; 6,81; 7,08; 7,02; 2,91};           

D. Biểu đồ trên không biểu thị cho ta một hàm số.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Từ biểu đồ đã cho, ta thấy ứng với mỗi thời điểm (năm) trong biểu đồ đều có một giá trị tốc độ tăng duy nhất.

Vì vậy biểu đồ trên biểu thị một hàm số.

Hàm số đó có:

+) Tập xác định D = {2016; 2017; 2018; 2019; 2020};

+) Tập giá trị T = {6,21; 6,81; 7,08; 7,02; 2,91}.

Vậy ta chọn phương án A.

Câu 9. Cho hàm số y = x² + 2x – 3 có đồ thị (P). Trục đối xứng của (P) là:

A. y = –1;

B. x = 1;

C. x = –1;

D. y = 1.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Hàm số đã cho có dạng y = ax² + bx + c, với a = 1, b = 2, c = –3.

Trục đối xứng của hàm số đã cho là đường thẳng $x=-\frac{b}{2a}=-\frac{2}{2.1}=-1$ (đường thẳng này đi qua đỉnh S và song song với trục Oy).

Vậy ta chọn phương án C.

Câu 10. Khi hàm số đồng biến trên tập xác định của nó thì đồ thị hàm số đó có dạng:

A. Đi lên từ phải sang trái;               

B. Đi xuống từ phải sang trái;          

C. Đi lên rồi đi xuống từ phải sang trái;              

D. Đi xuống rồi đi lên từ phải sang trái.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Khi hàm số đồng biến (tăng) trên tập xác định của nó thì đồ thị của hàm số đó có dạng đi lên từ trái sang phải hay có dạng đi xuống từ phải sang trái.

Vậy ta chọn phương án B.

II. Thông hiểu

Câu 1Cho hàm số $f\left(x\right)=\sqrt{2x-7}$ Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên $\left(\frac{7}{2};+\infty \right)$

B. Hàm số đồng biến trên $\left(\frac{7}{2};+\infty \right)$

C. Hàm số đồng biến trên ℝ;           

D. Hàm số nghịch biến trên ℝ.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Biểu thức f(x) có nghĩa khi và chỉ khi 2x – 7 ≥ 0.

Tức là khi $x\ge \frac{7}{2}$

Tập xác định của hàm số D = $\left[\frac{7}{2};+\infty \right)$

Lấy x₁, x₂ là hai số tùy ý thuộc D sao cho x₁ < x₂, ta có: x₁ < x₂.

Suy ra 2x₁ < 2x₂.

Khi đó 0 ≤ 2x₁ – 7 < 2x₂ – 7.

Vì vậy $\sqrt{2x_1-7}<\sqrt{2x_2-7}$

Do đó f(x₁) < f(x₂).

Vậy hàm số đồng biến trên D hay hàm số đồng biến trên $\left(\frac{7}{2};+\infty \right)$

Do đó ta chọn phương án B.

Câu 2. Cho hàm số $y=h\left(x\right)=\left\{\begin{array}{l}-2\left(x^2+1\right),khix\le 1\\ 4\sqrt{x-1},khix>1\end{array}\right.$. Khi đó $h\left(\frac{\sqrt{2}}{2}\right)$  bằng:

A. 2;          

B. 3;           

C.  –3;                 

D. 6.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Vì $\frac{\sqrt{2}}{2}<1$ nên ta có $h\left(\frac{\sqrt{2}}{2}\right)=-2\left[{\left(\frac{\sqrt{2}}{2}\right)}^2+1\right]=-3$

Vậy ta chọn đáp án C.

Câu 3. Cho hàm số y = f(x) xác định trên đọa [–3; 3] và có đồ thị được biểu diễn như hình bên:

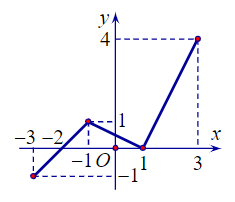
Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên (–1; 2);           

B. Hàm số đồng biến trên (–3; –1) và (1; 4);                

C. Hàm số đồng biến trên (–3; 3);             

D. Hàm số đồng biến trên (–3; –1) và (1; 3).

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Quan sát đồ thị ta thấy:

⦁ Trên khoảng (–3; –1), đồ thị có dạng đi lên từ trái sang phải nên hàm số đồng biến trên khoảng (–3; –1).

⦁ Trên khoảng (–1; 1), đồ thị có dạng đi xuống từ trái sang phải nên hàm số nghịch biến trên khoảng (–1; 1).

⦁ Trên khoảng (1; 3), đồ thị có dạng đi lên từ trái sang phải nên hàm số đồng biến trên khoảng (1; 3).

Phương án A sai vì hàm số đồng biến trên khoảng (1; 2).

Phương án B sai vì hàm số không xác định trên khoảng (3; 4).

Phương án C sai vì hàm số nghịch biến trên khoảng (–1; 1).

Phương án D đúng.

Vậy ta chọn phương án D.

Câu 4. Cho hàm số y = ax² + bx + c có đồ thị như hình vẽ:

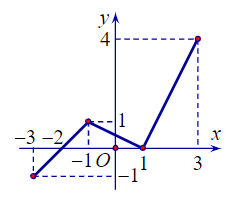
Mệnh đề nào dưới đây đúng?

A. a < 0, b > 0, c > 0;             

B. a > 0, b > 0, c > 0;             

C. a < 0, b < 0, c > 0;             

D. a < 0, b > 0, c < 0.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

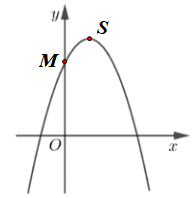
Vì đồ thị là một parabol có bề lõm quay xuống dưới nên a < 0.

Vì đỉnh S của parabol nằm bên phải trục Oy nên ta có hoành độ của đỉnh S là một số dương.

Nghĩa là, $\frac{-b}{2a}>0$

Mà a < 0.

Suy ra –b < 0.

Do đó b > 0.

Ngoài ra, parabol cắt trục Oy tại điểm M có tung độ là c > 0.

Vậy a < 0, b > 0, c > 0.

Do đó ta chọn đáp án A.

Câu 5. Điểm nào sau đây thuộc đồ thị hàm số $y=\frac{2x-1}{x\left(3x-4\right)}$

A. M(0; 1);          

B. $N\left(2;-\frac{3}{4}\right)$          

C. $P\left(\frac{4}{3};0\right)$

D. $Q\left(-2;-\frac{1}{4}\right)$

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Ta đặt $f\left(x\right)=\frac{2x-1}{x\left(3x-4\right)}$

Biểu thức f(x) có nghĩa khi và chỉ khi x(3x – 4) ≠ 0.

Tức là khi x ≠ 0 và 3x – 4 ≠ 0.

Do đó x ≠ 0 và $x\ne \frac{4}{3}$

Vì vậy hàm số có tập xác định là $D=ℝ\backslash \left\{0;\frac{4}{3}\right\}$

Các điểm M, P có hoành độ lần lượt là 0 và $\frac{4}{3}$đều không thuộc tập xác định D của hàm số đã cho.

Do đó ta loại phương án A, C.

⦁ Ta xét điểm $N\left(2;-\frac{3}{4}\right)$ , ta có hoành độ 2 ∈ D.

Ta có $f\left(2\right)=\frac{2.2-1}{2\left(3.2-4\right)}=\frac{3}{4}\ne -\frac{3}{4}$

Do đó điểm $N\left(2;-\frac{3}{4}\right)$  không thuộc đồ thị hàm số $y=\frac{2x-1}{x\left(3x-4\right)}$

Vì vậy ta loại phương án B.

⦁ Ta xét điểm $Q\left(-2;-\frac{1}{4}\right)$ , ta có –2 ∈ D.

Ta có $f\left(-2\right)=\frac{2.\left(-2\right)-1}{-2\left[3.\left(-2\right)-4\right]}=-\frac{1}{4}$

Do đó điểm $Q\left(-2;-\frac{1}{4}\right)$  thuộc đồ thị hàm số $y=\frac{2x-1}{x\left(3x-4\right)}$

Vậy ta chọn phương án D.

Câu 6. Giá trị m để đồ thị hàm số y = 2x – m + 6 đi qua điểm H(2; –5) là:

A. m = –6;           

B. m = 15;           

C. m = 8;             

D. m = 1.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Đồ thị hàm số y = 2x – m + 6 đi qua điểm H(2; –5).

Ta suy ra –5 = 2.2 – m + 6.

Tức là, m = 15.

Vậy ta chọn phương án B.

Câu 7. Đồ thị hàm số y = –x² + 2x + 3 cắt trục hoành tại mấy điểm?

A. 0;          

B. 3;           

C. 1;           

D. 2.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Cách 1:

Hàm số đã cho có dạng y = ax² + bx + c, với a = –1, b = 2, c = 3.

∆ = b² – 4ac = 2² – 4.(–1).3 = 16 > 0.

Suy ra phương trình –x² + 2x + 3 = 0 có 2 nghiệm x₁, x₂ phân biệt.

Vì vậy đồ thị hàm số bậc hai y = –x² + 2x + 3 cắt trục hoành tại hai điểm lần lượt có hoành độ là x₁, x₂.

Vậy ta chọn phương án D.

Cách 2:

Vẽ đường thẳng y = 0 biểu diễn như trong hình dưới đây:

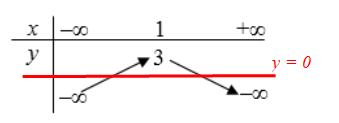
Do đó đồ thị hàm số cắt trục hoành (y = 0) tại hai điểm phân biệt.

Câu 8. Hàm số bậc hai có bảng biến thiên như hình vẽ dưới đây là:

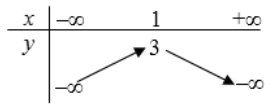
A. y = –2x² + 4x + 1;             

B. y = –x² + 4x + 2;                

C. y = 2x² – 4x + 5;                

D. y = x² – 2x + 1.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

⦁ Quan sát bảng biến thiên, ta thấy hàm số đồng biến trên khoảng (–∞; 1) và nghịch biến trên khoảng (1; +∞).

Vì vậy ta có a < 0.

Do đó ta loại phương án C, D.

⦁ Quan sát bảng biến thiên, ta thấy khi x = 1 thì y = 3.

Thay x = 1, y = 3 vào hàm số ở phương án A, ta được:

3 = –2.1² + 4.1 + 1 (đúng).

Thay x = 1, y = 3 vào hàm số ở đáp án B, ta được:

3 = –1² + 4.1 + 2 (vô lí).

Vậy ta chọn phương án A.

Câu 9. Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}-2x+1,khix\le -3\\ \frac{x+7}{2},khix>-3\end{array}\right.$ . Nếu f(x₀) = 5 thì x₀ bằng:

A. –2;                  

B. 3;           

C. 0;           

D. 1.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Trường hợp 1: x₀ ≤ –3.

Ta có f(x₀) = 5.

⇔ –2x₀ + 1 = 5.

⇔ –2x₀ = 4.

⇔ x₀ = –2.

So với điều kiện x₀ ≤ –3, ta loại x₀ = –2.

Trường hợp 2: x₀ > –3.

Ta có f(x₀) = 5.

$\iff \frac{x_0+7}{2}=5$

⇔ x₀ + 7 = 10.

⇔ x₀ = 3.

So với điều kiện x₀ > –3, ta nhận x₀ = 3.

Vì vậy nếu f(x₀) = 5 thì x₀ = 3.

Vậy ta chọn phương án B.

Câu 10. Xác định các hệ số m, n để parabol (P): y = mx² + 4x – n (m ≠ 0) có đỉnh S(–1; –5).

A. m = 3, n = –2;          

B. m = 3, n = 2;            

C. m = 2, n = 3;            

D. m = 2, n = –3.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Hàm số đã cho có dạng y = ax² + bx + c, với a = m, b = 4, c = –n  (m ≠ 0).

Ta có x_S = –1. Suy ra $\frac{-b}{2a}=-1$

Tức là $\frac{-4}{2m}=-1$

Khi đó –2m = –4.

Vì vậy m = 2.

Lại có đỉnh S(–1; –5) nằm trên parabol (P).

Suy ra –5 = m.(–1)² + 4.(–1) – n.

Khi đó m – n = –1.

Vì vậy 2 – n = –1.

Do đó n = 3.

Vậy m = 2, n = 3 thỏa mãn yêu cầu bài toán.

Do đó ta chọn phương án C.

Câu 11. Xét tính đồng biến, nghịch biến của hàm số $y=\sqrt[3]{x}+3$

A. Hàm số đã cho đồng biến trên tập xác định;            

B. Hàm số đã cho nghịch biến trên tập xác định;         

C. Hàm số đã cho vừa đồng biến, vừa nghịch biến trên tập xác định;                 

D. Không thể xác định được hàm số đồng biến hay nghịch biến trên tập xác định.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Xét hàm số $y=f\left(x\right)=\sqrt[3]{x}+3$

Tập xác định của hàm số này là D = ℝ.

Lấy x₁, x₂ tùy ý thuộc ℝ sao cho x₁ < x₂, ta có: x₁ < x₂.

Suy ra $\sqrt[3]{x_1}<\sqrt[3]{x_2}$

Khi đó ta có  $\sqrt[3]{x_1}+3<\sqrt[3]{x_2}+3$

Do đó f(x₁) < f(x₂).

Vì vậy hàm số đã cho đồng biến (tăng) trên ℝ.

Vậy ta chọn phương án A.

Câu 12. Cho hàm số y = 2x² – 4x + 3 có đồ thị là parabol (P). Mệnh đề nào sau đây sai?

A. (P) không có giao điểm với trục hoành;          

B. (P) có đỉnh là S(1; 1);                  

C. (P) có trục đối xứng là đường thẳng y = 1;               

D. (P) đi qua điểm M(–1; 9).

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

+ Gọi điểm A là giao điểm của parabol (P) và trục hoành.

Suy ra y_A = 0.

Vì A ∈ (P) nên $0=2x_A^2-4x_A+3$  (vô nghiệm).

Do đó không có điểm A là giao điểm của parabol (P) và trục hoành.

Vì vậy phương án A đúng.

+ Hàm số đã cho có dạng y = ax² + bx + c, với a = 2, b = –4, c = 3.

Đỉnh S có tọa độ:

⦁ $x_S=-\frac{b}{2a}=-\frac{-4}{2.2}=1$

⦁ y_S = 2.1² – 4.1 + 3 = 1.

Suy ra (P) có đỉnh S(1; 1) và có trục đối xứng là x = 1.

Do đó phương án B đúng, C sai.

+ Thay tọa độ điểm M vào hàm số của đồ thị (P) ta được:

9 = 2.(–1)² – 4.(–1) + 3 (đúng).

Suy ra (P) đi qua điểm M(–1; 9).

Do đó phương án D đúng.

Vậy ta chọn phương án C.

Câu 13. Cho hàm số y = –x² – x – 1. Tập giá trị của hàm số đã cho là:

A.$T=\left(-\infty ;\frac{3}{4}\right]$

B. $T=\left(-\infty ;-\frac{3}{4}\right]$

C. $T=\left(-\infty ;-\frac{3}{4}\right]$

D. $T=\left(-\infty ;-\frac{3}{4}\right)$

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Hàm số đã cho có dạng y = ax² + bx + c, với a = b = c = –1.

Ta có ∆ = b² – 4ac = (–1)² – 4.(–1).(–1) = –3.

Suy ra  $\frac{-\Delta }{4a}=\frac{-\left(-3\right)}{4.\left(-1\right)}=-\frac{3}{4}$

Vì a = –1 < 0 nên hàm số có giá trị lớn nhất bằng $-\frac{3}{4}$ và có tập giá trị là $T=\left(-\infty ;-\frac{3}{4}\right]$

Vậy ta chọn phương án B.

Câu 14. Đồ thị dưới đây là của hàm số nào sau đây?

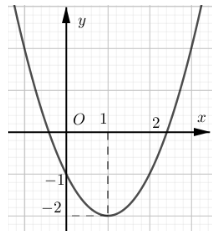
A. y = –x² – 2x + 3;                

B. y = x² + 2x – 2;                  

C. y = 2x² – 4x – 2;                

D. y = x² – 2x – 1.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

+ Quan sát đồ thị, ta thấy parabol có bề lõm quay lên trên nên a > 0.

Do đó ta loại phương án A vì a = –1 < 0.

+ Quan sát đồ thị, ta thấy parabol có trục đối xứng là đường thẳng x = 1.

⦁ Ở phương án B, đồ thị của hàm số y = x² + 2x – 2 có trục đối xứng là đường thẳngV

Do đó ta loại phương án B.

⦁ Ở phương án C, đồ thị của hàm số y = 2x² – 4x – 2 có trục đối xứng là đường thẳng $x=-\frac{b}{2a}=-\frac{-4}{2.2}=1$

• Ở phương án D, đồ thị của hàm số y = x² – 2x – 1 có trục đối xứng là đường thẳng $x=-\frac{b}{2a}=-\frac{-2}{2.1}=1$

+ Quan sát đồ thị, ta thấy parabol đi qua điểm A(0; –1).

• Thay x = 0, y = –1 vào hàm số ở phương án C, ta có: –1 = 2.0² – 4.0 – 2 (vô lí).

Do đó đồ thị của hàm số ở phương án C không đi qua điểm A(0; –1).

Vì vậy ta loại phương án C.

• Thay x = 0, y = –1 vào hàm số ở phương án D, ta có –1 = 0² – 2.0 – 1 (đúng).

Do đó đồ thị của hàm số ở phương án D đi qua điểm A(0; –1).

Vậy ta chọn phương án D.

Câu 15. Hàm số y = –x² + 2x + 3 có đồ thị là hình nào trong các hình sau?

A.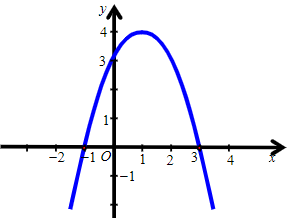 

B.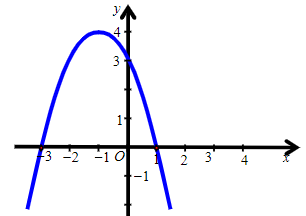 

C.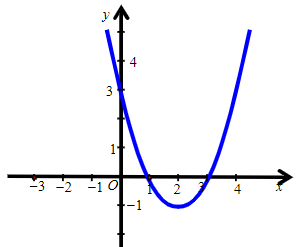 

D.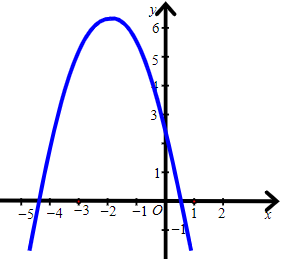 

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Cách 1:

Hàm số đã cho có dạng y = ax² + bx + c, với a = –1, b = 2, c = 3.

Ta có ∆ = b² – 4ac = 4 – 4.(–1).3 = 16.

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x² + 2x + 3 là một parabol (P):

⦁ Đỉnh S có tọa độ: $x_S=-\frac{b}{2a}=-\frac{2}{2.\left(-1\right)}=1$ và $y_S=-\frac{\Delta }{4a}=-\frac{16}{4.\left(-1\right)}=4$

Suy ra tọa độ đỉnh S(1; 4).

⦁ Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy).

⦁ Có bề lõm quay xuống dưới vì a = –1 < 0.

⦁ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

Ngoài ra, phương trình –x² + 2x + 3 = 0 có hai nghiệm phân biệt x₁ = 3 và x₂ = –1 nên đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có tọa độ (3; 0) và (–1; 0).

Ta vẽ được đồ thị sau:

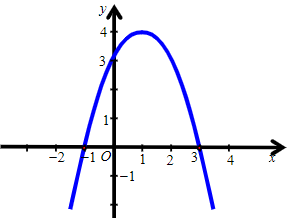
Vậy ta chọn phương án A.

Cách 2:

• Xét hàm số y = –x² + 2x + 3 có a = –1, b = 2, c = 3.

Vì a = –1 < 0 nên đồ thị có bề lõm quay xuống dưới.

Do đó ta loại phương án C.

• Đỉnh S có tọa độ: $x_S=-\frac{b}{2a}=-\frac{2}{2.\left(-1\right)}=1$ và $y_S=-\frac{\Delta }{4a}=-\frac{16}{4.\left(-1\right)}=4$

Suy ra tọa độ đỉnh S(1; 4).

Do đó ta loại phương án B và D.

Vậy ta chọn phương án A.

III. Vận dụng

Câu 1. Cho parabol y = ax² + bx + 4 có trục đối xứng là đường thẳng  và đi qua điểm A(1; 3). Tổng giá trị a + 2b bằng:

A. $–\frac{1}{2}$

B. 1        

C. $\frac{1}{2}$

D. –1.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Vì parabol có trục đối xứng là đường thẳng x =$\frac{1}{3}$ nên ta có $-\frac{b}{2a}=\frac{1}{3}$

Suy ra –3b = 2a.

Tức là, 2a + 3b = 0    (1)

Theo đề, ta có parabol đi qua điểm A(1; 3).

Suy ra 3 = a.1² + b.1 + 4.

Khi đó a + b + 4 = 3.

Do đó a + b = –1        (2)

Từ (1), (2), ta có hệ phương trình: $\left\{\begin{array}{l}2a+3b=0\\ a+b=-1\end{array}\right.$

$\iff \left\{\begin{array}{l}a=-3\\ b=2\end{array}\right.$

Vì vậy a + 2b = –3 + 2.2 = 1.

Vậy ta chọn phương án B.

Câu 2. Cho hàm số f(x) = ax² + bx + c (a, b, c ≠ 0) có đồ thị như hình vẽ bên.

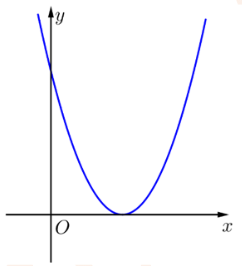
Biết f(c) = c. Giá trị của b là:

A. b = –6;            

B. b = –2;            

C. $b=-\frac{5}{2}$

D. b = –4.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Quan sát đồ thị, ta thấy parabol cắt trục hoành tại đỉnh của parabol hay parabol cắt trục hoành tại một điểm duy nhất.

Nghĩa là, phương trình ax² + bx + c = 0 có nghiệm kép.

Do đó ∆ = 0.

Suy ra b² – 4ac = 0   (1)

Ta có f(c) = c.

Suy ra ac² + bc + c = c.

Khi đó c(ac + b) = 0.

Vì vậy ac + b = 0 (vì c ≠ 0).

Do đó $c=-\frac{b}{a}$   (vì a ≠ 0).

Thay $c=-\frac{b}{a}$  vào (1) ta được: $b^2-4.a.\left(-\frac{b}{a}\right)=0$

Khi đó b² + 4b = 0 $\iff$ b(b + 4) = 0.

Vì vậy b = 0 hoặc b = –4.

Vì b ≠ 0 nên ta nhận b = –4.

Vậy ta chọn phương án D.

Câu 3. Biết rằng hàm số y = ax² + bx + c (a ≠ 0) đạt giá trị nhỏ nhất bằng 4 tại x = 2 và có đồ thị đi qua điểm A(0; 6). Giá trị biểu thức P = abc bằng

A. –6;                  

B. –3;                  

C. 6;           

D. $\frac{3}{2}$

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Ta có giá trị nhỏ nhất của hàm số bằng 4 tại x = 2.

Tức là đỉnh S(2; 4) và a > 0.

Suy ra 4 = a.2² + b.2 + c.

Do đó 4a + 2b + c = 4   (1)

Ta có x_S = 2.

Suy ra $-\frac{b}{2a}=2$

Do đó –b = 4a   (2)

Đồ thị hàm số đi qua điểm A(0; 6).

Suy ra 6 = a.0² + b.0 + c.

Do đó c = 6       (3)

Thay (2), (3) vào (1), ta được: –b + 2b + 6 = 4.

Suy ra b = –2.

Với b = –2, thay vào (2) ta được 4a = 2.

Suy ra  (thỏa mãn a > 0).

Vì vậy ta có , b = –2, c = 6.

Khi đó P = abc = $\frac{1}{2}.\left(-2\right).6=-6$

Vậy ta chọn phương án A.

Câu 4. Cho hàm số$y=f\left(x\right)=\frac{x+2}{x^2+1}$. Gọi (C) là đồ thị của hàm số đã cho và điểm M(m + 1; 1). Giá trị của tham số m để điểm M nằm trên đồ thị (C) là:

A. $m=\frac{1+\sqrt{5}}{2}$

B. $m=\frac{-1+\sqrt{5}}{2}$

C. $m=\frac{-1-\sqrt{5}}{2}$

D. Cả B và C đều đúng.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Vì M(m + 1; 1) ∈ (C) nên ta có $1=\frac{m+1+2}{{\left(m+1\right)}^2+1}$  (vì (m + 1)² + 1 > 0, ∀m ∈ ℝ)

Tức là (m + 1)² + 1 = m + 3.

Khi đó m² + m – 1 = 0.

Suy ra $\left[\begin{array}{l}m=\frac{-1+\sqrt{5}}{2}\\ m=\frac{-1-\sqrt{5}}{2}\end{array}\right.$

Vậy ta chọn phương án D.

Câu 5. Cho hàm số $f\left(x\right)=\sqrt{16-x^2}+\sqrt{2023x+2024m}$  (với m là tham số). Để tập xác định của hàm số chỉ có đúng một phần tử thì $m=\frac{a}{b}$  (a ∈ ℤ, b ∈ ℕ^*), với $\frac{a}{b}$ là phân số tối giản. Giá trị a + b bằng

A. –1517;            

B. 1517;              

C. 6068;              

D. –6068.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Biểu thức f(x) có nghĩa khi và chỉ khi .$\left\{\begin{array}{l}16-x^2\ge 0\\ 2023x+2024m\ge 0\end{array}\right.$

Tức là, $\left\{\begin{array}{l}-4\le x\le 4\\ x\ge -\frac{2024m}{2023}\end{array}\right.$

Do đó tập xác định của hàm số là D = $\left\{\begin{array}{l}-4\le x\le 4\\ x\ge -\frac{2024m}{2023}\end{array}\right.$

Ta có tập xác định của hàm số đã cho chỉ có đúng một phần tử.

Nghĩa là, D = $\left[-4;4\right]\cap \left[-\frac{2024m}{2023};+\infty \right)$  chỉ có đúng một phần tử.

$\iff 4=-\frac{2024m}{2023}\iff$–2024m = 8092.

Do đó $m=-\frac{2023}{506}$

Vì vậy a = –2023 và b = 506 (vì a ∈ ℤ, b ∈ ℕ^*).

Vậy a + b = –2023 + 506 = –1517.

Do đó ta chọn phương án A.

Câu 6. Biết rằng hàm số y = f(x) = x³ + 2x + 1 đồng biến trên ℝ. Đặt $A={\left(\frac{x^2+3}{x^2+1}\right)}^3+2\left(\frac{x^2+3}{x^2+1}\right)$  và $B=\frac{8}{{\left(x^2+1\right)}^3}+\frac{4}{x^2+1}$ . Khẳng định nào sau đây đúng?

A. A > B;            

B. A = B;             

C. A < B;             

D. A ≤ B.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Ta có $B=\frac{8}{{\left(x^2+1\right)}^3}+\frac{4}{x^2+1}={\left(\frac{2}{x^2+1}\right)}^3+2.\frac{2}{x^2+1}$

Ta đặt $x_1=\frac{2}{x^2+1}$  và $x_2=\frac{x^2+3}{x^2+1}$

Ta có $x_2=\frac{x^2+3}{x^2+1}=\frac{x^2+1+2}{x^2+1}=\frac{x^2+1}{x^2+1}+\frac{2}{x^2+1}=1+\frac{2}{x^2+1}>\frac{2}{x^2+1}$

Ta suy ra x₂ > x₁ hay x₁ < x₂.

Vì hàm số đã cho đồng biến trên ℝ và x₁ < x₂ nên ta có f(x₁) < f(x₂).

Suy ra ${\left(\frac{2}{x^2+1}\right)}^3+2.\frac{2}{x^2+1}+1<{\left(\frac{x^2+3}{x^2+1}\right)}^3+2.\frac{x^2+3}{x^2+1}+1$

Do đó ${\left(\frac{2}{x^2+1}\right)}^3+2.\frac{2}{x^2+1}<{\left(\frac{x^2+3}{x^2+1}\right)}^3+2.\frac{x^2+3}{x^2+1}$

Vì vậy B < A hay A > B.

Vậy ta chọn phương án A.

Câu 7. Một cửa hàng buôn giày nhập một đôi với giá là 40 USD. Cửa hàng ước tính rằng nếu đôi giày được bán với giá x USD thì mỗi tháng khách hàng sẽ mua (120 – x) đôi. Hỏi cửa hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?

A. 80 USD;         

B. 160 USD;                 

C. 40 USD;         

D. 240 USD.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Số tiền lãi khi bán một đôi giày của cửa hàng là: x – 40 (USD).

Gọi y là số tiền lãi của cửa hàng bán giày khi cửa hàng bán được x đôi giày.

Ta có y = (120 – x).(x – 40) = –x² + 160x – 4 800.

Hàm số đã cho có dạng y = ax² + bx + c, với a = –1, b = 160, c = –4 800.

∆ = b² – 4ac = 160² – 4.(–1).(–4 800) = 6 400.

Vì a = –1 < 0 nên hàm số đạt giá trị lớn nhất bằng $\frac{-\Delta }{4a}$ tại $x=\frac{-b}{2a}$

Khi đó $y_{max}=\frac{-6400}{4.\left(-1\right)}=1600$  khi $x=\frac{-160}{2.\left(-1\right)}=80$*

Vậy cửa hàng lãi nhiều nhất khi bán đôi giày với giá 80 USD.

Vậy ta chọn phương án A.

Câu 8. Dây truyền đỡ trên cầu treo có dạng parabol ACB như hình vẽ. Đầu, cuối của dây được gắn vào các điểm A, B trên mỗi trục AA’ và BB’ với độ cao 30 m. Chiều dài A’B’ trên nền cầu bằng 200 m. Gọi Q’, P’, H’, C’, I’, J’, K’ là các điểm chia đoạn A’B’ thành các phần bằng nhau (C’ chia đoạn A’B’ thành hai phần bằng nhau). Các thanh thẳng đứng nối nền cầu với đáy dây truyền: QQ’, PP’, HH’, CC’, II’, JJ’, KK’ gọi là các dây cáp treo.

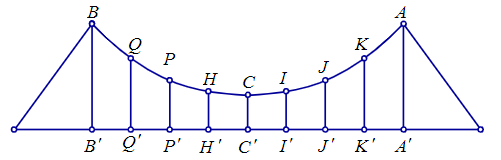
Biết độ cao ngắn nhất của dây truyền trên cầu là C’C = 5 m. Tổng độ dài của các dây cáp treo là:

A. 36,87 m;         

B. 73,75 m;         

C. 78,75 m;         

D. Đáp án khác.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

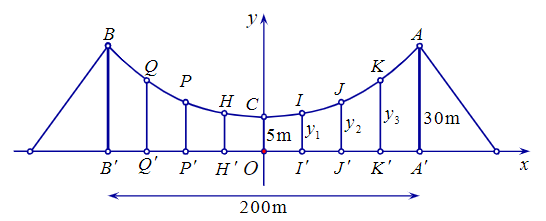
Giả sử parabol có dạng y = ax² + bx + c, với a ≠ 0.

Chọn hệ trục Oxy như hình vẽ. Khi đó O ≡ C’ là trung điểm A’B’.

Suy ra OA = OB = 100 (m).

Do đó parabol đi qua điểm A(100; 30).

Suy ra 30 = a.100² + b.100 + c.

Khi đó 10 000a + 100b + c = 30    (1)

Khi chọn hệ trục Oxy như hình vẽ, ta có Oy là trục đối xứng của parabol.

Vì C là giao điểm của trục đối xứng Oy và parabol.

Nên C là đỉnh của parabol.

Parabol có đỉnh C(0; 5).

Ta suy ra 5 = a.0² + b.0 + c.

Do đó c = 5

Ta có x_C = 0.

Suy ra $\frac{-b}{2a}=0$

Do đó b = 0.

Thay b = 0, c = 5 vào (1) ta được 10 000a + 100.0 + 5 = 30.

Suy ra a = $\frac{1}{400}\ne 0$

Vậy parabol có hàm số $y=\frac{1}{400}{x}^2+5$

Đoạn A’B’ được chia thành 8 phần bằng nhau.

Suy ra OI’ = I’J’ = J’K’ = $\frac{200}{8}$  = 25 (m).

Khi đó ta có $\left\{\begin{array}{l}O{I}^{‘}=25\\ O{J}^{‘}=25.2=50\\ O{K}^{‘}=25.3=75\end{array}\right.$

Do đó x_I’ = 25, x_J’ = 50, x_K’ = 75.

Với x_I’ = 25, ta có $y_1=y_{I^{‘}}=\frac{1}{400}{.25}^2+5=\frac{105}{16}$

Với x_J’ = 50, ta có $y_2=y_{J^{‘}}=\frac{1}{400}{.50}^2+5=\frac{45}{4}$

Với x_K’ = 75, ta có $y_3=y_{K^{‘}}=\frac{1}{400}{.75}^2+5=\frac{305}{16}$

Vậy tổng độ dài của các dây cáp treo bằng:

OC + 2y₁ + 2y₂ + 2y₃

$=5+2.\frac{105}{16}+2.\frac{45}{4}+2.\frac{305}{16}=\frac{315}{4}=78,75$ (m)

Vậy ta chọn phương án C.

Câu 9. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học phát hiện ra rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ có cân nặng P(n) = 360 – 10n. Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lượng cá sau một vụ thu được nhiều nhất?

A. 3 240;             

B. 40;                  

C. 20;                  

D. 18.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Gọi T là trọng lượng tất cả số con cá trên một đơn vị diện tích của mặt hồ.

Vì trên một diện tích của mặt hồ có n con cá nên ta có:

T = (360 – 10n).n = –10n² + 360n.

Hàm số T có dạng T = an² + bn + c, với a = –10, b = 360, c = 0.

∆ = b² – 4ac = 360² – 4.(–10).0 = 129 600.

Vì a = –10 < 0 nên hàm số đạt giá trị lớn nhất bằng  tại .

Khi đó $T_{\max }=\frac{-129600}{4.\left(-10\right)}=3240$ khi $n=\frac{-360}{2.\left(-10\right)}=18$

Vậy phải thả 18 con cá trên một đơn vị diện tích để trọng lượng cá sau một vụ thu được nhiều nhất.

Câu 10. Một chiếc cổng hình parabol có phương trình . Biết cổng có chiều rộng d = 5 m. Chiều cao h của cổng bằng:

A. 4,45 m;           

B. 3,125 m;         

C. 4,125 m;         

D. 3,25 m.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

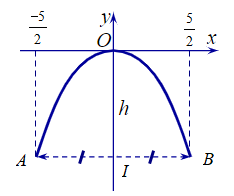
Gọi A và B là hai điểm ứng với chân cổng như hình vẽ.

Vì cổng hình parabol có phương trình $y=-\frac{1}{2}{x}^2$  và có chiều rộng d = 5 (m) nên ta có: AB = 5.

Gọi I là trung điểm AB. Suy ra IA = IB = $\frac{AB}{2}=\frac{5}{2}$  (m).

Hàm số đã cho có dạng y = ax² + bx + c, với $a=-\frac{1}{2}$, b = c = 0.

Vì b = 0 nên Oy là trục đối xứng của parabol.

Do đó trung điểm I của đoạn thẳng AB nằm trên Oy.

Khi đó điểm I có hoành độ bằng 0.

Vì IA = IB = $\frac{5}{2}$  nên ta có $x_A=-\frac{5}{2},x_B=\frac{5}{2}$

Với $x_A=-\frac{5}{2}$ , ta có $y_A=-\frac{1}{2}.{\left(-\frac{5}{2}\right)}^2=-\frac{25}{8}$

Suy ra tọa độ $A\left(-\frac{5}{2};-\frac{25}{8}\right)$

Với $x_B=\frac{5}{2}$ , ta có $y_B=-\frac{1}{2}.{\left(\frac{5}{2}\right)}^2=-\frac{25}{8}$

Suy ra tọa độ $A\left(-\frac{5}{2};-\frac{25}{8}\right)$

Vì vậy chiều cao h của cổng là:

h = OI = |y_A| = |y_B| = $\left|-\frac{25}{8}\right|=\frac{25}{8}=3,125$  (m).

Vậy ta chọn phương án B.

Xem thêm các bài trắc nghiệm Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Bài 2: Hàm số bậc hai

Trắc nghiệm Ôn tập chương 3

Trắc nghiệm Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°

Trắc nghiệm Bài 2: Bài tập Định lí côsin và định lí sin

Trắc nghiệm Bài 3: Giải tam giác và ứng dụng thực tế