Trắc nghiệm Toán 10 Bài 2: Tập hợp
I. Nhận biết
Câu 1. Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp (1; 4]?
A. ![]()
B. 
C. 
D. 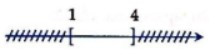
Hướng dẫn giải
Đáp án: A
Giải thích:
Tập hợp (1; 4] là tập hợp gồm các số thực sao cho 1 < x ≤ 4.
Tập hợp (1; 4] có dạng nửa khoảng (a; b], với a = 1, b = 4.
Do đó khi biểu diễn tập hợp (1; 4] trên trục số, ta thu được hình vẽ:
![]()
Vậy ta chọn phương án A.
Câu 2. Tập hợp X = {2; 7} có bao nhiêu phần tử?
A. 4;
B. 3;
C. 2;
D. Vô số.
Hướng dẫn giải
Đáp án: C
Giải thích:
Tập hợp X gồm có 2 phần tử là 2 và 7.
Do đó ta chọn phương án C.
Câu 3. Kí hiệu nào sau đây là để chỉ 5 là số tự nhiên?
A. 5 ⊂ ℕ;
B. 5 ∈ ℕ;
C. 5 ∉ ℕ;
D. 5 = ℕ.
Hướng dẫn giải
Đáp án: B
Giải thích:
Để chỉ 5 là phần tử của tập hợp ℕ (tập hợp số tự nhiên).
Ta viết 5 ∈ ℕ (đọc là 5 thuộc tập hợp số tự nhiên).
Do đó ta chọn phương án B.
Câu 4. Kí hiệu nào sau đây là để chỉ ![]() không phải là số hữu tỉ?
không phải là số hữu tỉ?
A. ![]() ;
;
B. ![]() ;
;
C. ![]() ;
;
D. Kí hiệu khác.
Hướng dẫn giải
Đáp án: C
Giải thích:
Để chỉ ![]() không phải là phần tử của tập hợp số hữu tỉ ℚ.
không phải là phần tử của tập hợp số hữu tỉ ℚ.
Ta viết ![]() (đọc là
(đọc là ![]() không thuộc tập hợp số hữu tỉ).
không thuộc tập hợp số hữu tỉ).
Do đó ta chọn phương án C.
Câu 5. Cho tập hợp A. Trong các mệnh đề sau, mệnh đề nào viết sai?
A. A ∈ ∅;
B. ∅ ⊂ A;
C. A ⊂ A;
D. ∅ ⊂ ∅.
Hướng dẫn giải
Đáp án: A
Giải thích:
Phương án A sai vì A là tập hợp, ∅ là tập rỗng. Mà kí hiệu giữa hai tập hợp ta không dùng “∈”.
Phương án B và D đúng vì tập rỗng là tập con của mọi tập hợp.
Phương án C đúng vì mọi tập hợp đều có tập con là chính nó.
Vậy ta chọn phương án A.
Câu 6. Cho hai tập hợp M và N. Hình nào sau đây minh họa M là tập con của N?
A. 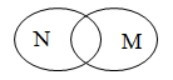
B. 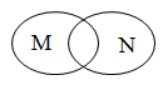
C. 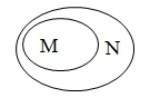
D. 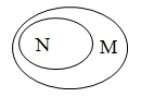
Hướng dẫn giải
Đáp án: C
Giải thích:
Theo đề, ta có quan hệ bao hàm: M là tập con của N hay M ⊂ N.
Nên khi vẽ biểu đồ Ven, ta sẽ vẽ đường cong kín biểu diễn tập hợp M nằm gọn trong đường cong kín biểu diễn tập hợp N.
Ta thấy chỉ có biểu đồ ở phương án C thỏa mãn yêu cầu.
Do đó ta chọn phương án C.
Câu 7. Cho tập hợp A = {x ∈ ℝ | –3 < x < 1}. Tập A là tập nào sau đây?
A. {–3; 1};
B. [–3; 1];
C. [–3; 1);
D. (–3; 1).
Hướng dẫn giải
Đáp án: D
Giải thích:
Ta thấy A là một tập con của tập số thực ℝ.
Do đó ta có thể dùng kí hiệu đoạn, khoảng, nửa khoảng để biểu diễn tập hợp A.
Ta thấy tập hợp A có dạng: {x ∈ ℝ | a < x < b}, với a = –3; b = 1.
Do đó ta có thể sử dụng kí hiệu khoảng (a; b) để biểu diễn tập hợp A.
Vậy ta có biểu diễn tập hợp A như sau: A = (–3; 1).
Ta chọn phương án D.
II. Thông hiểu
Câu 1. Tính chất đặc trưng của tập hợp H = {1; 2; 3; 4; 5}.
A. {x ∈ ℕ | x ≤ 5};
B. {x ∈ ![]() | x ≤ 5};
| x ≤ 5};
C. {x ∈ ℤ | x ≤ 5};
D. {x ∈ ℝ | x ≤ 5}.
Hướng dẫn giải
Đáp án: B
Giải thích:
⦁ Các phần tử của tập hợp ở phương án A là: {0; 1; 2; 3; 4; 5}.
Ta thấy phần tử 0 ∉ H.
Do đó tập hợp ở phương án A khác tập H.
⦁ Các phần tử của tập hợp ở phương án B là: {1; 2; 3; 4; 5} = H.
Do đó phương án B đúng.
⦁ Ta thấy phần tử –1 thuộc tập hợp ở đáp án C, D.
Nhưng –1 ∉ H.
Do đó tập hợp ở phương án C, D khác tập H.
Vậy ta chọn phương án B.
Câu 2. Cho tập hợp P = {1; 3} và tập hợp Q = {3; x}. Giá trị của x để P = Q là:
A. x = 1;
B. x = 2;
C. x = 3;
D. x = 5.
Hướng dẫn giải
Đáp án: A
Giải thích:
Ta thấy tập hợp P và Q đều có phần tử 3.
Tập P còn có phần tử 1.
Do đó để P = Q thì Q cần có thêm phần tử 1.
Nghĩa là, x = 1.
Vậy ta chọn phương án A.
Câu 3. Viết tập hợp D gồm các chữ cái có trong từ “TOKYO”.
A. D = {T; O; K; Y; O};
B. D = {K; T; Y; O};
C. D = {T; O; Y};
D. D = {K; Y; T}.
Hướng dẫn giải
Đáp án: B
Giải thích:
Các chữ cái trong từ “TOKYO” là: T; O; K; Y; O.
Do mỗi phần tử chỉ được liệt kê một lần nên ta có: T; O; K; Y.
Vậy tập hợp D ={T; O; K; Y}.
Do các phần tử có thể được viết theo thứ tự tùy ý.
Nên ta chỉ cần chọn tập hợp D ở phương án đã bao gồm đủ cả 4 phần tử T; O; K; Y.
Ta thấy đáp án B thỏa mãn yêu cầu.
Vậy ta chọn phương án B.
Câu 4. Cho A = {1; 2; 3}. Trong các khẳng định sau, khẳng định nào sai?
A. ∅ ⊂ A;
B. 1 ∈ A;
C. {1; 2} ⊂ A;
D. 2 = A.
Hướng dẫn giải
Đáp án: D
Giải thích:
Phương án A đúng vì tập rỗng là tập con của mọi tập hợp.
Phương án B đúng vì 1 là phần tử của A nên ta kí hiệu là 1 ∈ A.
Phương án C đúng vì {1; 2} là một tập hợp, các phần tử của tập hợp này đều thuộc tập hợp A nên tập hợp {1; 2} là tập con của tập hợp A, khi đó ta kí hiệu {1; 2} ⊂ A.
Phương án D sai kí hiệu. Sửa lại: 2 ∈ A.
Vậy ta chọn phương án D.
Câu 5. Cho bốn tập hợp E, F, G, K thỏa mãn E ⊂ F, F ⊂ G và G ⊂ K. Khẳng định nào sau đây đúng?
A. G ⊂ F;
B. K ⊂ G;
C. E = F = G;
D. E ⊂ K.
Hướng dẫn giải
Đáp án: D
Giải thích:
Ta có:
⦁ F ⊂ G nên phương án A sai.
⦁ G ⊂ K nên phương án B sai.
⦁ Giả sử E = {1; 2}, F = {1; 2; 3}, G = {1; 2; 3; 4}.
Ta thấy trong trường hợp trên, ta có E ⊂ F, F ⊂ G nhưng F ⊄ E vì 3 ∈ F nhưng 3 ∉ E.
Do đó phương án C không đúng trong mọi trường hợp.
⦁ Ta có quan hệ bao hàm: E ⊂ F, F ⊂ G và G ⊂ K.
Ta biểu diễn mối quan hệ giữa bốn tập hợp trên biểu đồ Ven như hình bên:
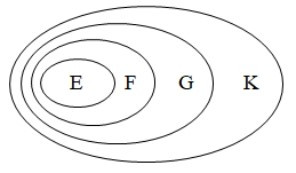
Quan sát biểu đồ Ven, ta thấy E ⊂ K.
Do đó phương án D đúng.
Vậy ta chọn phương án D.
Câu 6. Cho tập hợp H = {1; 2; 3; 4; x; y}. Xét các mệnh đề sau đây:
(I): “3 ∈ H”;
(II): “{3; 4} ∈ H”;
(III): “{x, 3, y} ∈ H”.
Trong các mệnh đề trên, mệnh đề nào đúng?
A. (I) đúng;
B. (I), (II) đúng;
C. (II), (III) đúng;
D. (I), (III) đúng.
Hướng dẫn giải
Đáp án: A
Giải thích:
⦁ Ta thấy 3 thuộc tập hợp A, ta kí hiệu là 3 ∈ A.
Do đó mệnh đề (I) đúng.
⦁ Vì kí hiệu “{3; 4}” là kí hiệu tập hợp nên mệnh đề (II) sai.
Do phần tử 3 và 4 đều thuộc tập hợp A nên ta có thể sửa lại kí hiệu là: {3; 4} ⊂ H.
⦁ Giải thích tương tự như mệnh đề (II), ta có mệnh đề (III) sai.
Vậy chỉ có mệnh đề (I) đúng.
Do đó ta chọn phương án A.
Câu 7. Cách viết nào sau đây đúng?
A. a ⊂ [a; b];
B. {a} ⊂ [a; b];
C. {a} ∈ [a; b];
D. a ∈ (a; b].
Hướng dẫn giải
Đáp án: B
Giải thích:
⦁ Ta sử dụng kí hiệu “∈” để biểu diễn một phần tử thuộc tập hợp.
Vì kí hiệu “a” là kí hiệu của phần tử, kí hiệu [a; b] là kí hiệu của tập hợp nên để biểu diễn a là phần tử thuộc tập hợp [a; b], ta kí hiệu là a ∈ [a; b].
Do đó kí hiệu ở phương án A sai.
⦁ Ta sử dụng kí hiệu “⊂” để biểu diễn một tập hợp là tập con của một tập hợp khác.
Vì kí hiệu {a} và [a; b] đều là kí hiệu của tập hợp và phần tử a thuộc tập hợp [a; b] nên ta kí hiệu là {a} ⊂ [a; b].
Do đó kí hiệu ở phương án B đúng.
⦁ Giải thích tương tự như phương án B, ta thu được phương án C sai.
Sửa lại: {a} ⊂ [a; b].
⦁ Vì phần tử a không thuộc tập hợp (a; b] nên kí hiệu ở phương án D sai.
Sửa lại: a ∉ (a; b].
Vậy ta chọn phương án B.
Câu 8. Cho tập hợp A = {x; y; z} và B = {x; y; z; t; u}. Tập hợp X nào trong các tập X dưới đây thỏa mãn A ⊂ X ⊂ B?
A. X = {x; y; z; t; u; v};
B. X = {x; y; z; t};
C. X = {y; t; u};
D. X = {t; u}.
Hướng dẫn giải
Đáp án: B
Giải thích:
Tập A là tập con của tập B khi mọi phần tử của tập hợp A đều thuộc tập hợp B.
Ta thấy tập hợp A gồm 3 phần tử là: x; y; z.
Tập hợp B gồm 5 phần tử là: x; y; z; t; u.
Trong 4 phương án A, B, C, D, ta thấy tập X ở phương án A và B đều chứa cả 3 phần tử x; y; z, còn phương án C, D không chứa cả 3 phần tử x; y; z.
Nên ta loại phương án C, D.
Ta thấy tập X ở phương án A có phần tử v ∉ B.
Do đó tập X ở phương án A không phải tập con của tập B.
Ta thấy tập X ở phương án B có 4 phần tử là x; y; z; t đều thuộc tập B.
Do đó tập X ở phương án B là tập con của tập hợp B.
Vậy ta chọn đáp án B.
III. Vận dụng
Câu 1. Cho tập hợp A = {x ∈ ℝ| (x2 – 1)(x2 + 2) = 0}. Các phần tử của tập A là:
A. A = {–1; 1};
B. ![]() ;
;
C. A = {–1};
D. A = {1}.
Hướng dẫn giải
Đáp án: A
Giải thích:
Ta có (x2 – 1)(x2 + 2) = 0.
Û x2 – 1 = 0 hoặc x2 + 2 = 0 (vô nghiệm)
Û (x – 1)(x + 1) = 0
Û x – 1 = 0 hoặc x + 1 = 0
Û x = 1 hoặc x = –1.
Vì 1 ∈ ℝ và –1 ∈ ℝ nên ta có 1; –1 đều là phần tử của tập hợp A.
Ta kí hiệu A = {–1; 1}.
Vậy ta chọn phương án A.
Câu 2. Cho tập hợp M = {x ∈ ℝ | x là ước chung của 12 và 20}. Tổng S các phần tử của tập hợp M là:
A. 0;
B. 3;
C. 7;
D. 6.
Hướng dẫn giải
Đáp án: A
Giải thích:
Ta có:
⦁ Ư(12) = {±1; ±2; ±3; ±4; ±6; ±12}.
⦁ Ư(20) = {±1; ±2; ±4; ±5; ±10; ±20}.
Suy ra ƯC(12; 20) = {±1; ±2; ±4}.
Vì x ∈ ℝ nên ta thu được M = ƯC(12; 20) = {±1; ±2; ±4}.
Tập hợp M có 6 phần tử gồm: –1; 1; –2; 2; –4; 4.
Do đó tổng S = –1 + 1 – 2 + 2 – 4 + 4 = 0.
Vậy ta chọn phương án A.
Câu 3. Cho biết A = B. Khẳng định nào sau đây sai?
A. A = {1; 3} và B = {x ∈ ℝ | (x – 1)(x – 3) = 0};
B. A = {1; 3; 5; 7; 9} và B = {n ∈ ℕ | n = 2k + 1, k ∈ ℤ, 0 ≤ k ≤ 4};
C. A = {–1; 2} và B = {x ∈ ℝ |x2 – 2x – 3 = 0};
D. A = ∅ và B = {x ∈ ℝ | x2 + x + 1 = 0}.
Hướng dẫn giải
Đáp án: C
Giải thích:
⦁ Ta có (x – 1)(x – 3) = 0
Û x = 1 hoặc x = 3.
Vì x = 1 ∈ ℝ và x = 3 ∈ ℝ.
Nên B = {1; 3}.
Mà A = {1; 3}.
Do đó A = B.
Vì vậy phương án A đúng.
⦁ Vì k ∈ ℤ và 0 ≤ k ≤ 4 nên ta có k ∈ {0; 1; 2; 3; 4}.
Với k = 0, ta có n = 2k + 1 = 2.0 + 1 = 1 ∈ ℕ.
Với k = 1, ta có n = 2k + 1 = 2.1 + 1 = 3 ∈ ℕ.
Với k = 2, ta có n = 2k + 1 = 2.2 + 1 = 5 ∈ ℕ.
Với k = 3, ta có n = 2k + 1 = 2.3 + 1 = 7 ∈ ℕ.
Với k = 4, ta có n = 2k + 1 = 2.4 + 1 = 9 ∈ ℕ.
Suy ra B = {1; 3; 5; 7; 9}.
Mà A = {1; 3; 5; 7; 9}.
Do đó A = B.
Vì vậy đáp án B đúng.
⦁ Ta có x2 – 2x – 3 = 0.
Û x = 3 ∈ ℝ hoặc x = –1 ∈ ℝ.
Do đó B = {–1; 3}.
Mà A = {–1; 2} nên A ≠ B.
Vì vậy phương án C sai.
⦁ Ta có x2 + x + 1 = 0 (vô nghiệm).
Do đó B = ∅.
Mà A = ∅.
Suy ra A = B.
Do đó phương án D đúng.
Vậy ta chọn phương án C.
Câu 4. Cho tập hợp X = {x | x ∈ ℝ, 3|x| ≤ 9} thì X được biểu diễn là hình nào trong các hình dưới đây?
A. 
B. 
C. 
D. 
Hướng dẫn giải
Đáp án: B
Giải thích:
Ta có 3|x| ≤ 9.
Û |x| ≤ 3.
Û –3 ≤ x ≤ 3.
Do đó tập hợp X là tập hợp các số thực ℝ thỏa mãn –3 ≤ x ≤ 3.
Khi đó ta có thể viết lại tập hợp X như sau:
X = {x | x ∈ ℝ, –3 ≤ x ≤ 3}.
Ta thấy tập hợp X có dạng:
{x ∈ ℝ | a ≤ x ≤ b}, với a = –3; b = 3.
Do đó khi biểu diễn tập hợp X trên trục số, ta thu được hình vẽ:

Vậy ta chọn phương án B.
Câu 5. Cho tập A có n + 1 phần tử (n ∈ ℕ*). Số tập con của A có hai phần tử là:
A. n(n + 1);
B. 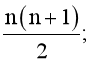
C. n + 1;
D. 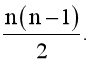
Hướng dẫn giải
Đáp án: B
Giải thích:
Lấy một phần tử của A ghép với n phần tử còn lại ta được n tập con có hai phần tử.
Vậy có (n + 1).n tập.
Nhưng mỗi tập con đó được tính hai lần do được lặp lại nên số tập con của A có hai phần tử là 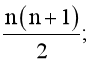
Vậy ta chọn phương án B.
Xem thêm các bài trắc nghiệm Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Trắc nghiệm Bài 1: Mệnh đề
Trắc nghiệm Bài 2: Tập hợp
Trắc nghiệm Bài 3: Các phép toán trên tập hợp
Trắc nghiệm Ôn tập chương 1
Trắc nghiệm Bài 1: Bất phương trình bậc nhất hai ẩn