20 câu Trắc nghiệm Nhị thức Newton (Chân trời sáng tạo 2023) có đáp án – Toán lớp 10

Trắc nghiệm Toán 10 Bài 3: Nhị thức Newton

I. Nhận biết

Câu 1. Số hạng tử trong khai triển (a + b)⁹⁹ bằng

A. 97;

B. 98; 

C. 99;

D. 100.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Ta có trong khai triển (a + b)ⁿ có n + 1 hạng tử

Vậy trong khai triển (a + b)⁹⁹ có 100 hạng tử

Câu 2. Hệ số tự do trong khai triển (x + 1)ⁿ với n ∈ ℤ, n ≥ 1 là:

A. n + 1;

B. n;

C. n – 1;

D. 1.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Ta có:

(x + 1)ⁿ

$=C_n^0.x^n{.1}^0+C_n^1.x^{n-1}{.1}^1+C_n^2.x^{n-2}{.1}^2+\mathrm{\dots }+C_n^{n-1}.x^1{.1}^{n-1}+C_n^n.x^0{.1}^n$

$=C_n^0.x^n+C_n^1.x^{n-1}+C_n^2.x^{n-2}+\mathrm{\dots }+C_n^{n-1}.x^1+C_n^n$

Do đó số hạng không chứa biến trong khai triển trên là $C_n^n=1.$

Vậy hệ số tự do của khai triển là 1.

Câu 3. Phát biểu nào sau đây đúng?

A. (a + b)⁴ = a⁴ – 4a³b + 6a²b² – 4ab³ + b⁴;         

B. (a – b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴;         

C. (a + b)⁴ = a⁴ + 4a³b – 6a²b² + 4ab³ + b⁴;         

D. (a – b)⁴ = a⁴ – 4a³b + 6a²b² – 4ab³ + b⁴.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Theo công thức nhị thức Newton, ta có:

⦁ (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.

Do đó phương án A, C sai.

⦁ (a – b)⁴ = a⁴ + 4a³(–b) + 6a²(–b)² + 4a(–b)³ + (–b)⁴

               = a⁴ – 4a³b + 6a²b² – 4ab³ + b⁴.

Do đó phương án B sai, phương án D đúng.

Vậy ta chọn phương án D.

Câu 4. Phát biểu nào sau đây đúng?

A. (a + b)⁵ = a⁵ + 5a⁴b – 10a³b² + 10a²b³ – 5ab⁴ + b⁵;            

B. (a – b)⁵ = a⁵ – 5a⁴b + 10a³b² – 10a²b³ + 5ab⁴ + b⁵;             

C. (a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵;            

D. (a – b)⁵ = a⁵ + 5a⁴b – 10a³b² + 10a²b³ – 5ab⁴ + b⁵.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Theo công thức nhị thức Newton, ta có:

⦁ (a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵.

Do đó phương án A sai, phương án C đúng.

⦁ (a – b)⁵ = a⁵ + 5a⁴(–b) + 10a³(–b)² + 10a²(–b)³ + 5a(–b)⁴ + (–b)⁵

               = a⁵ – 5a⁴b + 10a³b² – 10a²b³ + 5ab⁴ – b⁵.

Do đó phương án B, D sai.

Vậy ta chọn phương án C.

Câu 5. Biểu thức $C_4^0.x^4+C_4^1.x^{3}y+C_4^2.x^2{y}^2+C_4^3.x{y}^3+C_4^4.y^4$ bằng:

A. (x + y)⁴;          

B. (x – y)⁴;           

C. (x + y)⁵;          

D. (x – y)⁵.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Theo công thức nhị thức Newton, ta có:

$C_4^0.x^4+C_4^1.x^{3}y+C_4^2.x^2{y}^2+C_4^3.x{y}^3+C_4^4.y^4={\left(x+y\right)}^4$.

Vậy ta chọn phương án A.

Câu 6. Khai triển của biểu thức ${\left(2+\sqrt{5}\right)}^4$ là:

A. $2^4-{4.2}^3.\sqrt{5}+{6.2}^2.{\left(\sqrt{5}\right)}^2-\mathrm{4.2.}{\left(\sqrt{5}\right)}^3+{\left(\sqrt{5}\right)}^4$;            

B. $2^4+{4.2}^3.\sqrt{5}+{6.2}^2.{\left(\sqrt{5}\right)}^2+\mathrm{4.2.}{\left(\sqrt{5}\right)}^3+{\left(\sqrt{5}\right)}^4$;            

C. $2^4+{5.2}^3.\sqrt{5}+{10.2}^2.{\left(\sqrt{5}\right)}^2+\mathrm{5.2.}{\left(\sqrt{5}\right)}^3+{\left(\sqrt{5}\right)}^4$;          

D. $2^4+{4.2}^3.\sqrt{5}-{6.2}^2.{\left(\sqrt{5}\right)}^2+\mathrm{4.2.}{\left(\sqrt{5}\right)}^3+{\left(\sqrt{5}\right)}^4$.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Theo công thức nhị thức Newton, ta có:

${\left(2+\sqrt{5}\right)}^4=2^4+{4.2}^3.\sqrt{5}+{6.2}^2.{\left(\sqrt{5}\right)}^2+\mathrm{4.2.}{\left(\sqrt{5}\right)}^3+{\left(\sqrt{5}\right)}^4$.

Vậy ta chọn phương án B.

Câu 7. Tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (m + 2n)⁵ bằng

A. 4;

B. 5;

C. 6;

D. 7.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Ta có tổng số mũ của a, b trong mỗi hạng tử khi khai triển (a + b)ⁿ luôn bằng n.

Vậy tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (a + b)⁵ bằng 5.

II. Thông hiểu

Câu 1. Cho x là số thực dương, số hạng chứa x trong khai triển ${\left(x+\frac{2}{\sqrt{x}}\right)}^4$ là:

A. 24x;                

B. 12x;                 

C. 24;                  

D. 12.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích: 

Câu 2. Biết rằng trong khai triển ${\left(\frac{x}{2}+\frac{a}{x}\right)}^5$ (với x ≠ 0), hệ số của số hạng chứa $\frac{1}{x^3}$ là 640. Khi đó giá trị của a bằng:

A. a = 4;              

B. a = –4;            

C. n ∈ {–4; 4};

D. a ∈ ∅.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Cách 1: Ta có

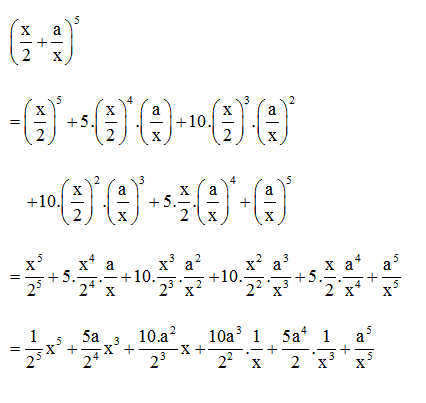
Cách 2:

Số hạng tổng quát trong khai triển ${\left(\frac{x}{2}+\frac{a}{x}\right)}^5$ là:

$C_5^k{\left(\frac{x}{2}\right)}^{5-k}{\left(\frac{a}{x}\right)}^k$ (với 0 ≤ k ≤ 5 và k ∈ ℤ).

$=C_5^k.\frac{x^{5-k}}{2^{5-k}}.\frac{a^k}{x^k}=\frac{C_5^k{a}^k}{2^{5-k}}.x^{5-2k}$

Để số hạng trên là số hạng chứa $\frac{1}{x^3}$ thì 5 – 2k = – 3  hay k = 4.

Khi đó ta có số hạng đó là $\frac{C_5^4{a}^4}{2^{5-4}}.x^{5-2.4}=\frac{5a^4}{2}.x^{-3}=\frac{5a^4}{2}.\frac{1}{x^3}$

Do đó hệ số của số hạng chứa ab³ trong khai triển ${\left(\frac{x}{2}+\frac{a}{x}\right)}^5$là $\frac{5a^4}{2}$.

Theo đề, ta có hệ số của số hạng chứa $\frac{1}{x^3}$ là 640.

Tức là, $\frac{5a^4}{2}=640$.

Tương tự như cách 1 ta tìm được a = 4 hoặc a = –4.

Vậy ta chọn phương án C.

Câu 3. Giá trị n nguyên dương thỏa mãn $A_n^2-C_{n+1}^{n-1}=5$ là:

A. n = –2;

B. n = 5;

C. n ∈ {–2; 5};

D. n ∈ ∅.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

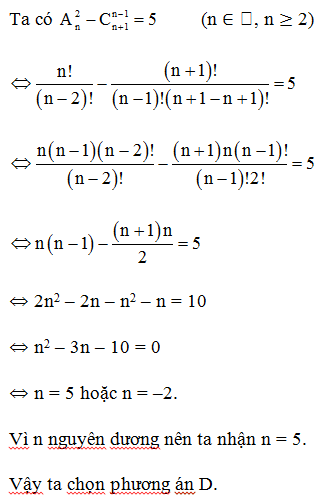
Câu 4. Số hạng chứa x³y trong khai triển ${\left(xy+\frac{1}{y}\right)}^5$ là:

A. 3x³y;               

B. 5x³y;               

C. 10x³y;             

D. 4x³y.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Cách 1: Ta có:

${\left(xy+\frac{1}{y}\right)}^5=C_5^0{\left(xy\right)}^5{\left(\frac{1}{y}\right)}^0+C_5^1{\left(xy\right)}^4{\left(\frac{1}{y}\right)}^1+C_5^2{\left(xy\right)}^3{\left(\frac{1}{y}\right)}^2+C_5^3{\left(xy\right)}^2{\left(\frac{1}{y}\right)}^3+C_5^4{\left(xy\right)}^1{\left(\frac{1}{y}\right)}^4+C_5^5{\left(xy\right)}^0{\left(\frac{1}{y}\right)}^5=x^5{y}^5+5x^4{y}^4.y^{-1}+10x^3{y}^3.y^{-2}+10x^2{y}^2.y^{-3}+5xy.y^{-4}+y^{–5}=x^5{y}^5+5x^4{y}^3+10x^{3}y+10x^2{y}^{-1}+5x{y}^{-3}+y^{-5}$

Vậy số hạng chứa x³y trong khai triển ${\left(xy+\frac{1}{y}\right)}^5$ là 10x³y.

Cách 2:

Số hạng tổng quát trong khai triển ${\left(xy+\frac{1}{y}\right)}^5$ là:

$C_5^k{\left(xy\right)}^{5-k}{\left(\frac{1}{y}\right)}^k$ (với 0 ≤ k ≤ 5 và k ∈ ℤ).

$=C_5^k{x}^{5-k}{y}^{5-k}{y}^{-k}=C_5^k{x}^{5-k}{y}^{5-2k}$

Để số hạng trên là số hạng chứa x³y thì $\left\{\begin{array}{l}5-k=3\\ 5-2k=1\end{array}\right.\iff k=2\left(tm\right)$

Khi đó ta có số hạng đó là $C_5^2{x}^{5-2}{y}^{5-2.2}=10x^{3}y$

Vậy số hạng chứa x³y trong khai triển ${\left(xy+\frac{1}{y}\right)}^5$ là 10x³y.

Do đó ta chọn phương án C.

Câu 5. Hệ số của số hạng chứa ab³ trong khai triển (a + 2b)⁴ là:

A. 32ab³;             

B. 32;                  

C. 8;           

D. 8ab³.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Cách 1: Ta có:

(a + 2b)⁴

= a⁴ + 4a³.2b + 6a².(2b)² + 4a.(2b)³ + (2b)⁴

= a⁴ + 8a³b + 24a²b² + 32ab³ + 16b⁴

Số hạng chứa ab³ trong khai triển (a + 2b)⁴ là: 32ab³.

Vậy hệ số chứa ab³ trong khai triển (a + 2b)⁴ là 32.

Do đó ta chọn phương án B.

Cách 2:

Số hạng tổng quát trong khai triển (a + 2b)⁴ là:

$C_4^k{a}^{4-k}{\left(2b\right)}^k$ (với 0 ≤ k ≤ 4 và k ∈ ℤ).

$=C_4^k{a}^{4-k}{2}^k{b}^k=2^k{C}_4^k{a}^{4-k}{b}^k$

Để số hạng trên là số hạng chứa ab³ thì $\left\{\begin{array}{l}4-k=1\\ k=3\end{array}\right.\iff k=3\left(tm\right)$

Khi đó ta có số hạng đó là $2^3{C}_4^3{a}^{4-3}{b}^3=32a^{3}b$

Vậy hệ số của số hạng chứa ab³ trong khai triển (a + 2b)⁴ là 32.

Câu 6. Số hạng không chứa x trong khai triển $P\left(x\right)={\left(x^3-\frac{1}{x^2}\right)}^5$ (x ≠ 0) (theo chiều số mũ của x giảm dần) là số hạng thứ:

A. 3;          

B. 6;           

C. 4;           

D. 5.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Theo nhị thức Newton, ta có:

$P\left(x\right)={\left(x^3-\frac{1}{x^2}\right)}^5={\left(x^3\right)}^5+5.{\left(x^3\right)}^4.\left(-\frac{1}{x^2}\right)+10.{\left(x^3\right)}^3.{\left(-\frac{1}{x^2}\right)}^2+10.{\left(x^3\right)}^2.{\left(-\frac{1}{x^2}\right)}^3+5.x^3.{\left(-\frac{1}{x^2}\right)}^4+{\left(-\frac{1}{x^2}\right)}^5=x^{15}-5.x^{12}.\frac{1}{x^2}+10.x^9.\frac{1}{x^4}-10.x^6.\frac{1}{x^6}+5.x^3.\frac{1}{x^8}-\frac{1}{x^{10}}=x^{15}-5.x^{10}+10.x^5-10+5.\frac{1}{x^5}-\frac{1}{x^{10}}$

Ta thấy số hạng không chứa x là số hạng thứ 4 (theo chiều số mũ của x giảm dần).

Vậy ta chọn phương án C.

Câu 7. Cho x là số thực dương. Khai triển nhị thức ${\left(x^2+\frac{1}{x}\right)}^4$, ta có hệ số của số hạng chứa x^m bằng 6. Giá trị của m là:

A. m = 6;             

B. m = 8;             

C. m = 2;             

D. m = 2 hoặc m = 6.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Theo công thức nhị thức Newton, ta có:

${\left(x^2+\frac{1}{x}\right)}^4={\left(x^2\right)}^4+4.{\left(x^2\right)}^3.\frac{1}{x}+6.{\left(x^2\right)}^2.{\left(\frac{1}{x}\right)}^2+4.x^2.{\left(\frac{1}{x}\right)}^3+{\left(\frac{1}{x}\right)}^4=x^8+4.x^6.\frac{1}{x}+6.x^4.\frac{1}{x^2}+4.x^2.\frac{1}{x^3}+\frac{1}{x^4}=x^8+4.x^5+6.x^2+4.\frac{1}{x}+\frac{1}{x^4}$.

Ta thấy số hạng có hệ số bằng 6 là 6x².

Suy ra m = 2.

Vậy ta chọn phương án C.

Câu 8. Giá trị của biểu thức ${\left(3+\sqrt{2}\right)}^4+{\left(3-\sqrt{2}\right)}^4$ bằng:

A. 193;                

B. –386;              

C. 772;                

D. 386.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Áp dụng công thức nhị thức Newton, ta có:

III. Vận dụng

Câu 1. Số hạng chính giữa trong khai triển (x³ + xy)²² là:

A. $C_{22}^{11}.x^{42}.y^{12}$;

B. $C_{22}^{13}.x^{41}.y^{11}$;

C. $C_{22}^{12}.x^{43}.y^{11}$;

D. $C_{22}^{12}.x^{42}.y^{12}$.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích:

Số hạng tổng quát của khai triển (x³ + xy)²² là:

$C_{22}^k{\left(x^3\right)}^{22-k}{\left(xy\right)}^k$ (với 0 ≤ k ≤ 22 và k ∈ ℤ)

$=C_{22}^k.x^{66-3k}.x^k.y^k=C_{22}^k.x^{66-2k}.y^k$

(x³ + xy)²² có số mũ là 22 nên khai triển này có 23 số hạng.

Do đó số hạng chính giữa là số hạng thứ 12 ứng với k = 11.

Vậy số hạng chính giữa của khai triển là $C_{22}^{12}.x^{42}.y^{12}$.

Câu 2. Cho tập hợp M = {1; 2; 3; 4}. Số tập con của tập M là:

A. 8;          

B. 16;                  

C. 32;                  

D. 5.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: B

Giải thích:

Ta thấy tập hợp M có 4 phần tử.

• Mỗi tập con của M có k phần tử (với 1 ≤ k ≤ 4) là một tổ hợp chập k của 4 phần tử.

Do đó số tập con như vậy bằng $C_4^k$.

• Mặt khác, có một tập con của M không có phần tử nào (tập rỗng).

Tức là, có $C_4^0=1$ tập con như vậy.

Do đó số tập con của tập hợp M là:

$C_4^0+C_4^1+C_4^2+C_4^3+C_4^4$ = 16 (tập con).

Vậy ta chọn phương án B.

Câu 3. Cho biểu thức (2 + x)ⁿ, biết n là số nguyên dương thỏa mãn $A_n^3+2A_n^2=100$. Khi đó số hạng của x³ trong khai triển biểu thức (2 + x)ⁿ là:

A. –40;                

B. –40x³;             

C. 40x³;               

D. 80x³.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

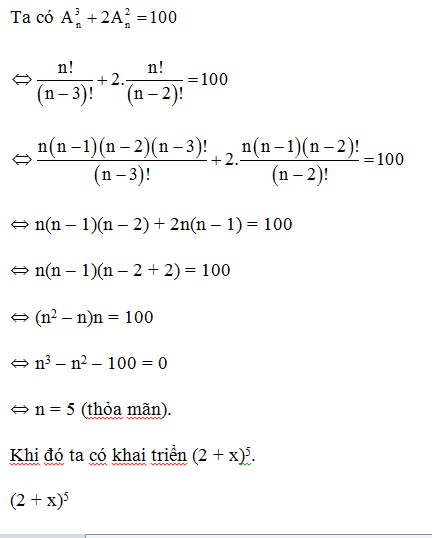
⇔ n(n – 1)(n – 2) + 2n(n – 1) = 100

⇔ n(n – 1)(n – 2 + 2) = 100

⇔ (n² – n)n = 100

⇔ n³ – n² – 100 = 0

⇔ n = 5 (thỏa mãn).

Khi đó ta có khai triển (2 + x)⁵.

(2 + x)⁵

= 2⁵ + 5.2⁴.x + 10.2³.x² + 10.2².x³ + 5.2.x⁴ + x⁵

= 32 + 80x + 80x² + 40x³ + 10x⁴ + x⁵

Vậy số hạng của x³ trong khai triển biểu thức (2 + x)⁵ là 40x³.

Do đó ta chọn phương án C.

Câu 4. Tổng $S=C_5^0+3C_5^1+3^2{C}_5^2+3^3{C}_5^3+3^4{C}_5^4+3^5{C}_5^5$ bằng:

A. S = 3⁵;            

B. S = 2⁵;             

C. S = 3.2⁵;          

D. S = 4⁵.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: D

Giải thích: 

Theo công thức nhị thức Newton, ta có:

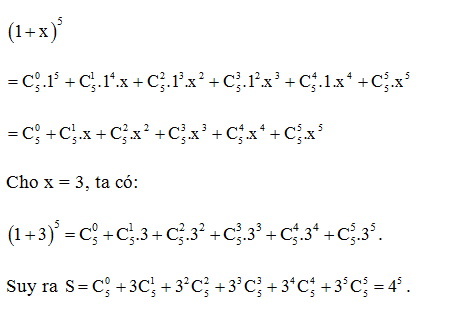
Vậy ta chọn phương án D.

Câu 5. Hệ số của số hạng x¹⁰ trong khai triển (1 + x + x² + x³)⁵ là:

A. 5;          

B. 50;                  

C. 101;                

D. 105.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: C

Giải thích:

Ta có (1 + x + x² + x³)⁵ = [1 + x + x²(1 + x)]⁵

         = [(1 + x)(1 + x²)]⁵ = (1 + x)⁵.(1 + x²)⁵.

Theo công thức nhị thức Newton, ta có:

⦁ A = (1 + x)⁵

= 1⁵ + 5.1⁴.x + 10.1³.x² + 10.1².x³ + 5.1.x⁴ + x⁵

= 1 + 5x + 10x² + 10x³ + 5x⁴ + x⁵.

⦁ B = (1 + x²)⁵

= 1⁵ + 5.1⁴.x² + 10.1³.(x²)² + 10.1².(x²)³ + 5.1.(x²)⁴ + (x²)⁵

= 1 + 5x² + 10x⁴ + 10x⁶ + 5x⁸ + x¹⁰.

Suy ra (1 + x + x² + x³)⁵ = A.B

Khi đó ta có số hạng chứa x¹⁰ trong khai triển (1 + x + x² + x³)⁵ là:

xⁱ.x^j = x¹⁰ hay x^{i + j} = x¹⁰ với xⁱ là lũy thừa của số hạng trong A, x^j là lũy thừa của số hạng trong B (i ∈ {0; 1; 2; 3; 4; 5} và j ∈ {0; 2; 4; 6; 8; 10}).

Do đó ta có bảng sau:

j	i
10	0
8	2
6	4

Từ bảng ta có số hạng chứa x¹⁰ trong khai triển là:

1.x¹⁰ + 10x².5x⁸ + 5x⁴.10x⁶

= x¹⁰ + 50x¹⁰ + 50x¹⁰ = 101x¹⁰.

Vậy hệ số của số hạng chứa x¹⁰ trong khai triển (1 + x + x² + x³)⁵ là 101.

Do đó ta chọn phương án C.

Xem thêm các bài trắc nghiệm Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Bài 2. Hoán vị, chỉnh hợp và tổ hợp

Trắc nghiệm Bài 3. Nhị thức Newton

Trắc nghiệm Ôn tập chương 8

Trắc nghiệm Toán 10 Bài 1: Toạ độ của vectơ

Trắc nghiệm Toán 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ