Sách bài tập Toán 12 Bài 10 (Kết nối tri thức): Phương sai và độ lệch chuẩn

Giải SBT Toán 12 Bài 10: Phương sai và độ lệch chuẩn

Bài 3.5 trang 65 SBT Toán 12 Tập 1: Cho mẫu số liệu ghép nhóm sau về thời gian ngủ trong ngày của các học sinh lớp 12A.

Tính số trung bình và độ lệch chuẩn cho mẫu số liệu ghép nhóm trên.

Lời giải:

Chọn giá trị đại diện cho mỗi nhóm dố liệu ta có mẫu số liệu sau:

Cỡ mẫu là: 5 + 12 + 15 + 3 = 35.

Số trung bình là:

$\overrightarrow{x}$ = $\frac{1}{35}$(5.6,75 + 12.7,25 + 15.7,75 + 3.8,35) ≈ 7,48.

Độ lệch chuẩn là:

s = $\sqrt{\frac{1}{35}\left(5.6,{75}^2+\mathrm{\dots }+3.8,{25}^2\right)-7,{48}^2}$ ≈ 0,39.

Bài 3.6 trang 66 SBT Toán 12 Tập 1: Chiều cao của 20 cây xoan giống (đơn vị là cm) được cho như sau:

a) Tính độ lệch chuẩn của s_g của mẫu số liệu.

b) Hoàn thiện bảng số liệu ghép nhóm sau và tính độ lệch chuẩn s_n của mẫu số liệu ghép nhóm này:

c) Nên dùng giá trị s_g hay s_n để đo mức độ phân tán về chiều cao của 20 cây giống xoan này?

Lời giải:

a) Tổng chiều cao 20 cây xoan giống đó là:

15 + 19 + 24 + 31 + 27 + 23 + 18 + 19 + 25 + 29 + 23 + 33 + 34 + 27 + 31 + 24 + 27 + 21 + 29 + 30 = 509.

Chiều cao trung bình của 20 cây xoan giống là: $\frac{509}{20}$ = 25,45.

Ta có: Tổng bình phương của 20 giá trị số liệu trong bảng là:

15² + 19² + 24² + 31² + 27² + 23² + 18² + 19² + 25² + 29² + 23² + 33² + 34² + 27² + 31² + 24² + 27² + 21² + 29² + 30² = 13 483.

Lúc này, độ lệch chuẩn của mẫu số liệu gốc là:

S_g = $\sqrt{\frac{1}{20}.13483-25,{45}^2}$ ≈ 5,14.

b) Ta có bảng số liệu ghép nhóm như sau:

Ta có bảng giá trị đại diện là:

Số trung bình là:

$\overline{x}$ = $\frac{4.17,5+5.22,5+6.27,5+5.32,5}{20}$ = 25,5.

Độ lệch chuẩn là:

s = $\sqrt{\frac{1}{20}\left(4.17,5^2+5.22,5^2+6.27,5^2+5.32,5^2\right)-25,5^2}$ ≈ 5,34.

c) Từ số liệu tính được phần a, b ta nên dùng giá trị s_g để đo mức độ phân tán về chiều cao của 20 cây xoan giống.

Bài 3.7 trang 66 SBT Toán 12 Tập 1: Độ lệch chuẩn của mỗi mẫu số liệu ghép nhóm sau cho biết điều gì?

a) Mẫu số liệu ghép nhóm về thành tích 20 lần luyện tập (đơn vị tính là phút) của mỗi vận động viên chạy cự li 1 000 mét.

b) Mẫu số liệu ghép nhóm về kết quả 20 lần đo khoảng cách từ Trái Đất đến một ngôi sao (đơn vị là năm ánh sáng) khi dùng một thiết bị đo mới được chế tạo.

Lời giải:

a) Độ lệch chuẩn của mẫu số liệu ghép nhóm về thành tích 20 lần luyện tập (đơn vị tính là phút) của một vận động viên chạy cự li 1 000 m cho biết mức độ ổn định trong thành tích của vận động viên này.

b) Độ lệch chuẩn của mẫu số liệu ghép nhóm về kết quả 20 lần đo khoảng cách từ Trái Đất đến một ngôi sao (đơn vị là năm ánh sáng) khi dùng một thiết bị đo mới được chế tạo cho biết độ chính xác của thiết bị này. Độ lệch chuẩn càng nhỏ thì thiết bị đo càng chính xác.

Bài 3.8 trang 66 SBT Toán 12 Tập 1: Doanh thu theo tháng của một cửa hàng trong hai năm 2022 và 2023 được cho như sau:

Tính độ lệch chuẩn của hai mẫu số liệu ghép nhóm và cho biết trong năm nào của hàng này có doanh thu hàng tháng ổn định hơn.

Lời giải:

Chọn giá trị đại diện cho mỗi nhóm ta có bảng số liệu sau:

Doanh thu trung bình một tháng của cửa hàng trong năm 2022 là:

$\overline{x}=\frac{1}{12}$(17,5.1 + 5.22,5 + 4.27,5 + 2.32,5) ≈ 25,42.

Doanh thu trung bình một tháng của cửa hàng trong năm 2023 là:

$\overline{x}=\frac{1}{12}$(3.17,5 + 4.22,5 + 3.27,5 + 2.32,5) ≈ 24,17.

Độ lệch chuẩn cho doanh thu các tháng năm 2022 là:

S₂₀₂₂ = $\sqrt{\frac{1}{12}\left(17,5^2+5.22,5^2+4.27,5^2+2.32,5^2\right)-25,{42}^2}$

≈ 4,29.

Độ lệch chuẩn cho doanh thu các tháng năm 2023 là:

S₂₀₂₃ = $\sqrt{\frac{1}{12}\left(3.17,5^2+4.22,5^2+3.27,5^2+2.32,5^2\right)-24,{17}^2}$

 ≈ 5,12.

Do đó s₂₀₂₂ < s₂₀₂₃.

Như vậy, doanh thu hằng tháng của cửa hàng trong năm 2022 ổn định hơn.

Bài 3.9 trang 66 SBT Toán 12 Tập 1: Lợi nhuận của 20 nhà đầu tư quy mô ở hai lĩnh vực A và B được cho như sau (lợi nhuận âm được hiểu là lỗ vốn):

Hỏi đầu tư vào lĩnh vực nào “rủi ro” hơn?

Lời giải:

Chọn giá trị đại diện cho bảng số liệu, ta có bảng sau:

Lợi nhuận trung bình của các nhà đầu tư vào lĩnh vực A là:

$\overline{x}=\frac{1}{20}\left[2.\left(-0,75\right)+3.\left(-0,25\right)+7.0,25+5.0,75+3.1,25\right]$ = 0,35.

Lợi nhuận trung bình của các nhà đầu tư vào lĩnh vực B là:

$\overline{x}=\frac{1}{20}\left[1.\left(-0,75\right)+3.\left(-0,25\right)+10.0,25+4.0,75+2.1,25\right]$ = 0,325.

Độ lệch chuẩn của lợi nhuận khi đầu tư vào lĩnh vực A là:

Độ lệch chuẩn của lợi nhuận khi đầu tư vào lĩnh vực B là:

Do s_A > s_B nên đầu tư vào lĩnh vực A rủi ro hơn lĩnh vực B.

Lý thuyết Phương sai và độ lệch chuẩn

1. Phương sai và độ lệch chuẩn

Cho mẫu số liệu ghép nhóm:

 

trong đó các tần số $m_1>0,m_k>0$ và $n=m_1+...+m_k$ là cỡ mẫu

Phương sai của mẫu số liệu ghép nhóm, kí hiệu là s2 , là một số được tính theo công thức sau: $$s^2=\frac{m{(x_1-\overline{x})}^2+...+m_k{(x_k-\overline{x})}^2}{n}$$ Trong đó, $n=m_1+...+m_k$; $x_i=\frac{a_i+a_{i+1}}{2}$ với I = 1,2,…,k là giá trị đại diện cho nhóm $\left[a_i;a_{i+1}\right)$ và $\overline{x}=\frac{m_1{x}_1+...+m_k{x}_k}{n}$ là số trung bình của mẫu số liệu ghép nhóm Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là $s=\sqrt{s^2}$

Ý nghĩa: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm là các xấp xỉ cho phương sai, độ lệch chuẩn của mẫu số liệu gốc. Chúng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Phương sai, độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán

2. Sử dụng phương sai, độ lệch chuẩn đo độ rủi ro

Ví dụ: Anh An đầu tư số tiền bằng nhau vào hai lĩnh vực kinh doanh A, B. Anh An thống kê số tiền thu được mỗi tháng trong vòng 60 ngày theo mỗi lĩnh vực có kết quả như sau:

 

So sánh giá trị trung bình và độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào mỗi lĩnh vực A, B. Đầu tư vào lĩnh vực nào “rủi ro” hơn?

Giải:

Chọn giá trị đại diện cho các nhóm số liệu ta có:

 

Số tiền trung bình thu được khi đầu tư vào các lĩnh vực A, B tương ứng là:

$\overline{x_A}=\frac{1}{60}(5.7,5+...+5.27,5)=17,5$ (triệu đồng)

$\overline{x_B}=\frac{1}{60}(20.7,5+...+20.27,5)=17,5$ (triệu đồng)

Như vậy, về trung bình đầu tư vào các lĩnh vực A, B số tiền thu được hàng tháng như nhau

Độ lệch chuẩn của số tiền thu được hàng tháng khi đầu tư vào các lĩnh vực A, B tương ứng là:

$s_A=\sqrt{\frac{1}{60}(5.7,5^2+...+5.27,5^2-17,5^2}=5$

$s_B=\sqrt{\frac{1}{60}(20.7,5^2+...+20.27,5^2-17,5^2}\approx 8,42$

Như vậy, độ lệch chuẩn của mẫu số liệu về số tiền thu được hàng tháng khi đầu tư vào lĩnh vực B cao hơn khi đầu tư vào lĩnh vực A. Người ta nói rằng, đầu tư vào lĩnh vực B là “rủi ro” hơn

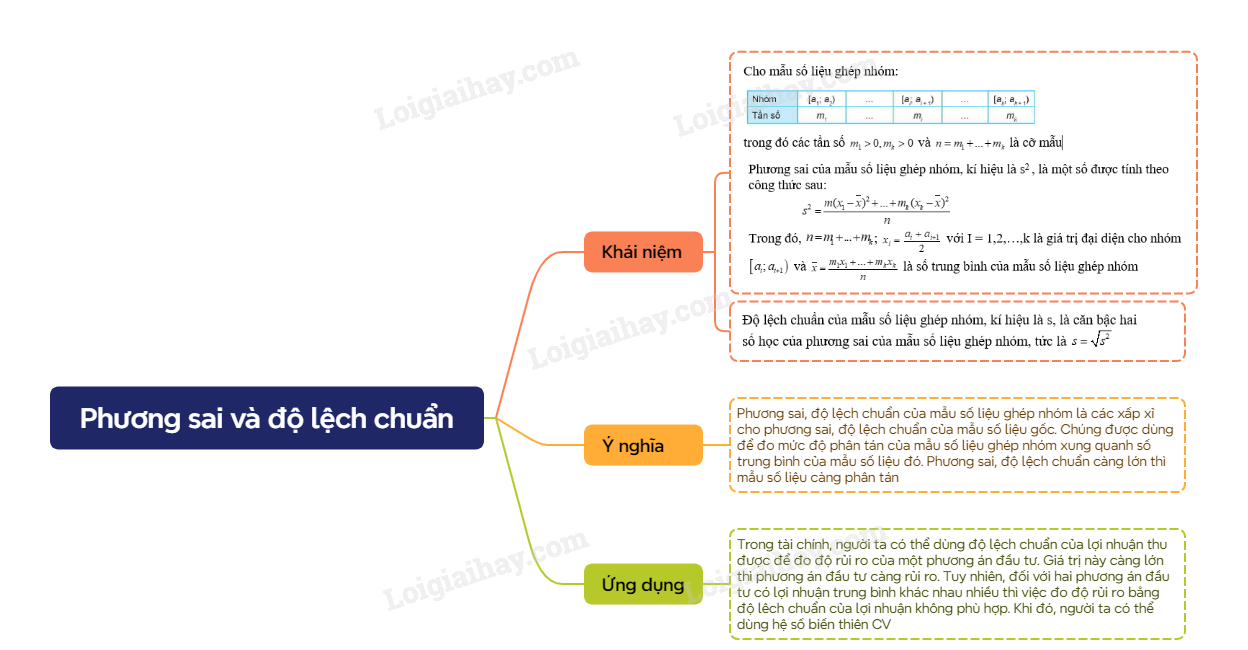
Sơ đồ tư duy Phương sai và độ lệch chuẩn

Xem thêm các bài giải SBT Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

Bài 9: Khoảng biến thiên và khoảng tứ phân vị

Bài 10: Phương sai và độ lệch chuẩn

Bài tập cuối chương 3

Bài 11: Nguyên hàm

Bài 12: Tích phân

Bài 13: Ứng dụng hình học của tích phân