Giải SBT Toán 12 Bài 9: Khoảng biến thiên và khoảng tứ phân vị
Bài 3.1 trang 62 SBT Toán 12 Tập 1: Cho mẫu số liệu ghép nhóm sau về chiều cao (tính từ mặt bầu cây) của 20 cây cam giống nhau:
a) Tìm khoảng biến thiên Rn cho mẫu số liệu ghép nhóm trên.
b) Biết rằng trong 20 cây cam giống trên, cây cao nhất là 72 cm và cây thấp nhất là 46 cm. Tìm khoảng biến thiên Rg cho mẫu số liệu gốc. Để đo độ phân tán của mẫu số liệu về chiều cao 20 cây cam giống ta dùng Rn hay Rg sẽ chính xác hơn?
Lời giải:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm là: Rn = 80 – 40 = 40.
b) Khoảng biến thiên của mẫu số liệu gốc là Rg = 72 – 46 = 26.
Để đo độ phân tán của mẫu số liệu về chiều cao của 20 cây cam giống này ta dùng Rg sẽ chính xác hơn.
Bài 3.2 trang 62 SBT Toán 12 Tập 1: Một trang trại thử nghiệm nuôi một giống cá mới. Sau 6 tháng người ta thu hoạch cho kết quả như sau:
a) Tìm khoảng tứ phân vị ∆Q của mẫu số liệu ghép nhóm.
b) Khoảng tứ phân vị của mẫu số liệu gốc có phụ thuộc vào cân nặng của 10 con cá có khối lượng nhỏ nhất không? Vì sao?
Lời giải:
a) Cỡ mẫu là n = 10 + 40 + 80 + 50 + 20 = 200.
Ta có: = 50 nên nhóm chứa tứ phân vị thứ nhất là [1,5 ;2).
Do đó, tứ phân vị thứ nhất là Q1 = 1,5 + = 2.
Ta có: = 150 nên nhóm chứa tứ phân vị thứ 3 là [2,5; 3).
Do đó, Q3 = 2,5 + = 2,7.
Vậy khoảng tứ phân vị là ∆Q = 2,7 – 2 = 0,7.
b) Gọi x1 ≤ x2 ≤ x3 ≤….≤ x200 là khối lượng của 200 con cá thì giá trị của khoảng tứ phân vị của mẫu số liệu gốc chỉ phụ thuộc vào x51, x52, x53,…., x150.
Do đó nó không phụ thuộc vào cân nặng của 10 con cá có khối lượng nhỏ nhất.
Bài 3.3 trang 62 SBT Toán 12 Tập 1: Kết quả thi thử của các thí sinh tại một trung tâm tiếng Anh được cho như sau:
a) Nêu các nhóm số liệu và tần số tương ứng. Giải thích thông tin của một nhóm số liệu.
b) Tìm khoảng tứ phân vị cho mẫu số liệu ghép nhóm.
Lời giải:
a) Các nhóm số liệu là: 26-30, 31-35, 36-40, 41-45, 46-50 với tần số tương ứng là 5, 15, 30, 20, 10.
Nhóm 26-30 có tần số 5 nghĩa là có 5 thí sinh có điểm tiếng Anh thuộc tập {26; 27; 28; 29; 30}. Tương tự với các nhóm còn lại.
b) Hiệu chỉnh các nhóm ta thu được bảng tần số ghép nhóm như sau:
Tổng số thí sinh là: n = 5 + 15 + 30 + 20 + 10 = 80.
Do = 20 nên Q1 = 35,5.
Ta có: = 60 nên nhóm chứa tứ phân vị thứ ba là [40,5; 50,5).
Do đó, Q3 = 40,5 + = 43.
Vậy, khoảng tứ phân vị là ∆Q = 43 – 35,5 = 7,5.
Bài 3.4 trang 62 SBT Toán 12 Tập 1: Bảng sau đây cho biết thành tích nhảy cao của các học sinh nam trong hai lớp 12A và 12B:
Hỏi nên dùng khoảng biến thiên hay khoảng tứ phân vị để so sánh mức độ phân tán của hai mẫu số liệu ghép nhóm trên? Tại sao?
Lời giải:
Từ bảng số liệu, ta thấy thành tích nhảy cao của các bạn lớp 12A có 1 giá trị bất thường thuộc [1,1; 1,2) và thành tích nhảy cao của các bạn lớp 12B có 1 giá trị bất thường thuộc nhóm [1,7; 1,8). Vì vậy ta nên dùng khoảng tứ phân vị để có thể loại bỏ ảnh hưởng của các giá trị bất thường này.
Lý thuyết Khoảng biến thiên và khoảng tứ phân vị
1. Khoảng biến thiên
Cho mẫu số liệu ghép nhóm:

trong đó các tần số và là cỡ mẫu
|
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là |
Ý nghĩa: Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc. Khoảng biến thiên được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán
2. Khoảng tứ phân vị
|
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là , là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất của mẫu số liệu đó, tức là |
Ý nghĩa: Do khoảng tứ phân vị của mẫu số liệu ghép nhóm chỉ phụ thuộc vào nửa giữa của mẫu số liệu, nên không bị ảnh hưởng bởi các giá trị bất thường và có thể dùng đại lượng này để loại giá trị bất thường
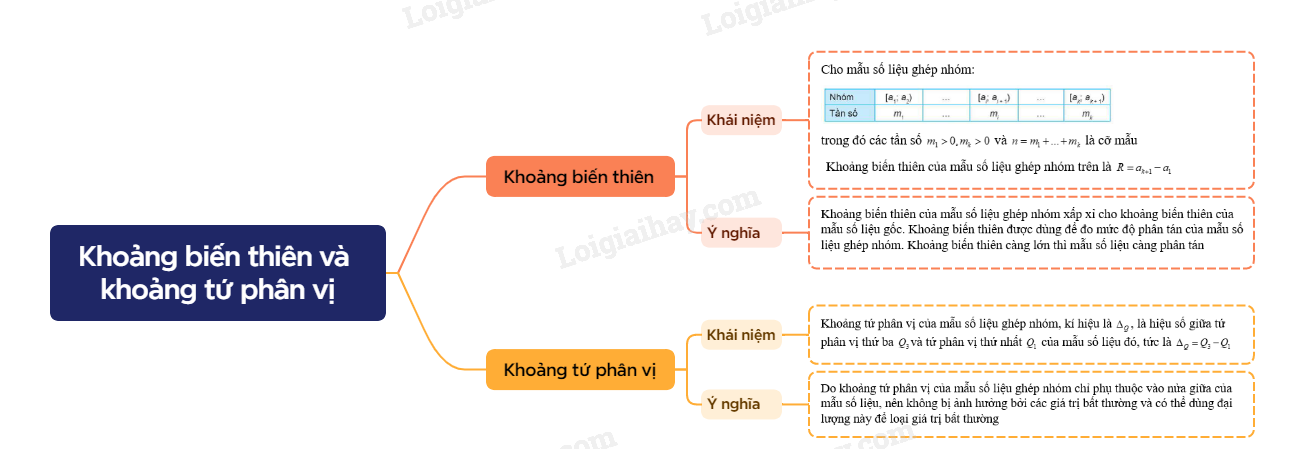
Sơ đồ tư duy Khoảng biến thiên và khoảng tứ phân vị
Xem thêm các bài giải SBT Toán lớp 12 Kết nối tri thức hay, chi tiết khác:
Bài tập cuối chương 2
Bài 9: Khoảng biến thiên và khoảng tứ phân vị
Bài 10: Phương sai và độ lệch chuẩn
Bài tập cuối chương 3
Bài 11: Nguyên hàm
Bài 12: Tích phân