Cho ∆ABC ngoại tiếp đường tròn (O). Gọi D, E, F là các tiếp điểm của đường tròn trên các cạnh AB, BC, CA. Gọi M, N, P lần lượt là giao điểm của đường tròn (O) với các tia OA, OB, OC. Chứng minh rằng các điểm M, N, P lần lượt là tâm đường tròn nội tiếp các tam giác ∆ADF, ∆BDE, ∆CEF

Câu hỏi:

Cho $∆\mathrm{ABC}$ ngoại tiếp đường tròn (O). Gọi D, E, F là các tiếp điểm của đường tròn trên các cạnh AB, BC, CA. Gọi M, N, P lần lượt là giao điểm của đường tròn (O) với các tia OA, OB, OC. Chứng minh rằng các điểm M, N, P lần lượt là tâm đường tròn nội tiếp các tam giác $∆\mathrm{ADF}$, $∆\mathrm{BDE}$, $∆\mathrm{CEF}$

Trả lời:

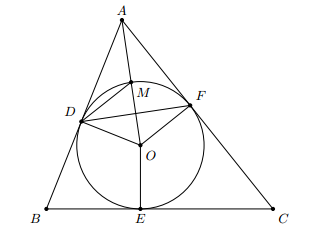Để chứng minh M là tâm đường tròn nội tiếp các tam giác ADF, ta chứng minh M là giao điểm của hai tia phân giác trong của tam giác ADF.AD là tiếp tuyến của đường tròn (O) nên AM là tia phân giác của $\widehat{\mathrm{DAF}}$ (1)Lại có, $\widehat{\mathrm{MDF}}=\widehat{\mathrm{MFD}}=\widehat{\mathrm{MDA}}$ nên DM là tia phân giác của $\widehat{\mathrm{ADF}}$ (2)Từ (1) và (2) suy ra M là tâm đường tròn nội tiếp các tam giác ADFChứng minh tương tự với các điểm N và P.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Từ một điểm M bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó. Chứng minh rằng MT2 = MA.MB
   
   

   Câu hỏi:
   

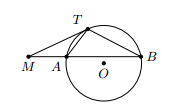
   Từ một điểm M bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó. Chứng minh rằng ${\mathrm{MT}}^2$ = MA.MB

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho đường tròn (O) và một điểm M nằm bên ngoài đường tròn. Tia Mx quay quanh M và cắt đường tròn tại hai điểm A và B. Gọi I là một điểm thuộc tia Mx sao cho MI2 = MA.MB. Tìm quỹ tích điểm I.
   
   

   Câu hỏi:
   

   Cho đường tròn (O) và một điểm M nằm bên ngoài đường tròn. Tia Mx quay quanh M và cắt đường tròn tại hai điểm A và B. Gọi I là một điểm thuộc tia Mx sao cho ${\mathrm{MI}}^2$ = MA.MB. Tìm quỹ tích điểm I.

   Trả lời:

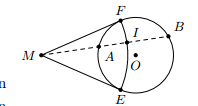   Phần thuận: Kẻ hai tiếp tuyến ME, MF tới đường tròn (O).Ta có ${\mathrm{ME}}^2={\mathrm{MF}}^2=\mathrm{MA}.\mathrm{MB}={\mathrm{MI}}^2$ nên $\mathrm{ME}=\mathrm{MF}=\mathrm{MI}$Suy ra I thuộc đường tròn (M; ME)Hạn chế quỹ tích: vì A chỉ chạy trên cung $\stackrel{⏜}{\mathrm{EF}}$ của đường tròn (O) nên I chỉ chạy trên cung $\stackrel{⏜}{\mathrm{EF}}$ của đường tròn (M,ME) nằm trong đường tròn (O)Phần đảo: lấy điểm I thuộc $\stackrel{⏜}{\mathrm{EF}}$ của đường tròn (M. ME) nằm trong đường tròn (O).Nối MI cắt đường tròn (O) tại A và B. Ta cần chứng minh $\mathrm{MA}.\mathrm{MB}={\mathrm{MI}}^2$. Thật vậy, ${\mathrm{MI}}^2={\mathrm{ME}}^2=\mathrm{MA}.\mathrm{MB}$Kết luận: vậy quỹ tích điểm I là cung $\stackrel{⏜}{\mathrm{EF}}$ của đường tròn (M, ME) nằm trong đường tròn (O).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho A, B, C là ba điểm cùng nằm trên một đường tròn. At là tiếp tuyến của đường tròn tại A. Đường thẳng song song với At cắt AB tại M và cắt AC tại N. Chứng minh rằng AB.AM = AC.AN.
   
   

   Câu hỏi:
   

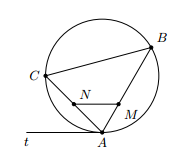
   Cho A, B, C là ba điểm cùng nằm trên một đường tròn. At là tiếp tuyến của đường tròn tại A. Đường thẳng song song với At cắt AB tại M và cắt AC tại N. Chứng minh rằng AB.AM = AC.AN.

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
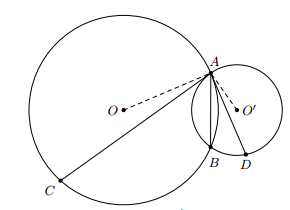
4. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Từ A vẽ hai tiếp tuyến với hai đường tròn. Hai tiếp tuyến này gặp đường tròn O ở C và đường tròn  (O’) ở D. Chứng minh rằng ABC^=ABD^
   
   

   Câu hỏi:
   

   Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Từ A vẽ hai tiếp tuyến với hai đường tròn. Hai tiếp tuyến này gặp đường tròn O ở C và đường tròn  (O’) ở D. Chứng minh rằng $\widehat{\mathrm{ABC}}=\widehat{\mathrm{ABD}}$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
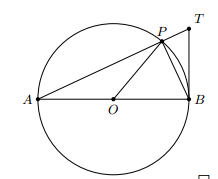
5. Cho đường tròn tâm (O) đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh rằng APO^=PBT^
   
   

   Câu hỏi:
   

   Cho đường tròn tâm (O) đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh rằng $\widehat{\mathrm{APO}}=\widehat{\mathrm{PBT}}$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====