Trên các cạnh của một hình bình hành, dựng về phía ngoài nó các hình vuông. Chứng minh rằng nếu nối tâm các hình vuông này, ta được một hình vuông.

Câu hỏi:

Trên các cạnh của một hình bình hành, dựng về phía ngoài nó các hình vuông. Chứng minh rằng nếu nối tâm các hình vuông này, ta được một hình vuông.

Trả lời:

Chú ý $\widehat{KAF}=\widehat{TCJ}$ (2 cạnh tương ứng song song)$\widehat{ABC}=\widehat{ADC}$ (góc đối của hình bình hành)$\widehat{FAK}=\widehat{ABC}$ (có cạnh tương ứng vuông góc)Suy ra $\widehat{KAF}=\widehat{TCJ} = \widehat{ABC}=\widehat{ADC}$Vậy $\widehat{MAQ}=\widehat{MBN}=\widehat{PCN}=\widehat{PDQ}$ Lại có: MA = MB = PC=PD và AQ = BN = CN = DQ(nửa đường chéo của hình vuông bằng nhau) Suy ra DMAQ = DMBN = DPCN = DPDQ Þ MQ = MN = NP = PQ (1)Do các tam giác bằng nhau $\Rightarrow \widehat{BNM}=\widehat{CNP}hay\widehat{BNC}=\widehat{MNP}$ = 90⁰ (2).Từ (1) và (2) có MNPQ là hình vuông

====== **** mời các bạn xem câu tiếp bên dưới **** =====

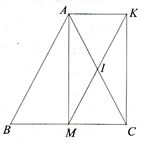
1. Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng của điểm M qua điểm I.a) Tứ giác AMCK là hình gì ?b) Tứ giác AKMB là hình gì ? c) Có trường hợp nào của tam giác ABC để tứ giác AKMB là hình thoi không ? Vì sao ?
   
   

   Câu hỏi:
   

   Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng của điểm M qua điểm I.a) Tứ giác AMCK là hình gì ?b) Tứ giác AKMB là hình gì ? c) Có trường hợp nào của tam giác ABC để tứ giác AKMB là hình thoi không ? Vì sao ?

   Trả lời:

   a) Áp dụng tính chất của tam giác cân cho DABC ta có: AM ^ MC và BM = MCI là trung điểm của AC và K đối xứng với M qua I nên tứ giác AMCK  là hình bình hànhLại có MK = AC (=2MI)Þ Tứ giác AMCK là hình chữ nhật.b) Vì tứ giác AMCK là hình chữ nhật (chứng minh ở a) Þ AK//MC và AK = MC = MB nên tứ giác AKMB là hình bình hành.c) Nếu tứ giác AKMB là hình thoi thì BA = AK = KM= MB.Þ DMBA cân tại B Þ $\widehat{BAM}=\widehat{AMB}$ = 90⁰ Þ vô lý.Vậy không có trường hợp nào của D ABC để AKMB là hình thoi.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho tam giác ABC vuông tại A, trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng của điểm M qua điểm D.a) Chứng minh điểm E đối xứng với điểm M qua đường thẳng AB.b) Các tứ giác AEMC, AEBM là hình gì ?c) Cho BC = 4 cm. Tính chu vi tứ giác AEBM.d) Tam giác vuông ABC thỏa điều kiện gì thì AEBM là hình vuông?
   
   

   Câu hỏi:
   

   Cho tam giác ABC vuông tại A, trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng của điểm M qua điểm D.a) Chứng minh điểm E đối xứng với điểm M qua đường thẳng AB.b) Các tứ giác AEMC, AEBM là hình gì ?c) Cho BC = 4 cm. Tính chu vi tứ giác AEBM.d) Tam giác vuông ABC thỏa điều kiện gì thì AEBM là hình vuông?

   Trả lời:

   a)Vì E đối xứng với điểm M qua điểm D nên M,D,E thẳng hàng và DM = DE (1)Áp dụng tính chất đường trung bình cho DBAC ta có DM//AC.Mà DABC vuông tại A nên CA ^ AB Þ MD ^ AB (2)Từ (1) và (2) Þ E đối xứng với M qua đường thẳng AB.b) Tứ giác AEMC là hình bình hành, tứ giác AEBM là hình thoi.c) Chu vi tứ giác AEBM là 4BM = 8 (cm)d) nếu tứ giác AEBM là hình vuông thì ME = AB mà ME = AC (do ACME là hình bình hành) Þ AC = AB Þ DABC vuông cân tại A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hình vuông ABCD. E là điểm trên cạnh DC, F là điểm trên tia đối của tia BC sao cho BF = DE.a) Chứng minh tam giác AEF vuông cân.b) Gọi I là trung điểm của EF. Chứng minh I thuộc BD.c) Lấy điểm K đối xứng với A qua I. Chứng minh tứ giác AEKF là hình vuông
   
   

   Câu hỏi:
   

   Cho hình vuông ABCD. E là điểm trên cạnh DC, F là điểm trên tia đối của tia BC sao cho BF = DE.a) Chứng minh tam giác AEF vuông cân.b) Gọi I là trung điểm của EF. Chứng minh I thuộc BD.c) Lấy điểm K đối xứng với A qua I. Chứng minh tứ giác AEKF là hình vuông

   Trả lời:

   a) DDAE = DBAF (c.g.c)$\Rightarrow \widehat{DAE}=\widehat{BAF}$ và AE = AFMà $\widehat{EAD}+\widehat{EAB}={90}^0 => \widehat{EAB}+\widehat{BAF}={90}^0$ Þ DAEF vuông cân tại A.b) DEAF vuông cân nên IA = IE = FI (1); DCFE vuông có IC là đường trung tuyến Þ IE = IC = IF (2);Từ (1) và (2) suy ra Þ IA = IC nên I thuộc trung trực của AC hay I thuộc BD.c) Do K đối xứng với A qua I nên I là trung điểm của AK.Mà I là trung điểm của EF(gt) nên AFKE là hình bình hành, DAEF vuông cân tại A nên AI ^ EF.Vậy AFKE là hình vuông.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến AM.          a) Chứng minh BAH^=MAC^.           b) Trên đường trung trực Mx của đoạn thẳng BC, lấy điểm D sao cho MD = MA (D và A thuộc hai nửa mặt phẳng đối nhau bờ BC). Chứng minh rằng AD là phân giác chung của MAH^&CAB^.          c) Từ D kẻ DE, DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình gì ?          d) Chứng minh ΔDBE=ΔDCF
   
   

   Câu hỏi:
   

   Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến AM.          a) Chứng minh $\widehat{BAH}=\widehat{MAC}.$           b) Trên đường trung trực Mx của đoạn thẳng BC, lấy điểm D sao cho MD = MA (D và A thuộc hai nửa mặt phẳng đối nhau bờ BC). Chứng minh rằng AD là phân giác chung của $\widehat{MAH}\&\widehat{CAB}.$          c) Từ D kẻ DE, DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình gì ?          d) Chứng minh $\Delta DBE=\Delta DCF$

   Trả lời:

   a)  $\widehat{BAH}+\widehat{MAC}$ vì cùng phụ với $\widehat{ABC}$b) $\widehat{A_1}=\widehat{C_1}$(1) (chứng minh a)Mà DABC vuông có AM là trung tuyến nên DAMC cân tại M $\widehat{C_1}=\widehat{A_4}$(2).Từ (1) và (2) suy ra $\widehat{A_1}=\widehat{A_4}$(3)D thuộc đường trung trực của BC.Þ DM ^ BC = {M}Þ $\widehat{D_1}=\widehat{A_2}$Vì DM = MA (giả thiết) $\Rightarrow \widehat{M_1}=\widehat{A_3}\Rightarrow \widehat{A_2}=\widehat{A_3}$(4)Từ (3) và (4) Þ AD là phân giác chung của $\widehat{MAH}\&\widehat{CAB}$c) Theo cách vẽ và kết quả câu b), ta có AEDF là hình vuông.d) DDBE = DDCF  (cạnh huyền – cạnh góc vuông)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình vuông ABCD. Gọi E là điểm đối xứng của điểm A qua điểm D.          a) Chứng minh tam giác ACE là tam giác vuông cân.          b) Từ A hạ AH ^ BE, gọi M và N theo thứ tự là trung điểm của AH và HE. Chứng minh tứ giác BMNC là hình bình hành.          c) Chứng minh M là trực tâm của tam giác ANB.          d) Chứng minh ANC^=900.
   
   

   Câu hỏi:
   

   Cho hình vuông ABCD. Gọi E là điểm đối xứng của điểm A qua điểm D.          a) Chứng minh tam giác ACE là tam giác vuông cân.          b) Từ A hạ AH ^ BE, gọi M và N theo thứ tự là trung điểm của AH và HE. Chứng minh tứ giác BMNC là hình bình hành.          c) Chứng minh M là trực tâm của tam giác ANB.          d) Chứng minh $\widehat{ANC}={90}^0.$

   Trả lời:

   a) E là điểm đối xứng của điểm A qua điểm D Þ A, D, E thẳng hàng và DA = DE Þ CD ^ AE tại trung điểm của AE Þ CA = CE Þ DCAE cân ở C.Þ $\widehat{DAC}$ = 45⁰ Þ DACE vuông cân.b) Áp dụng tính chất đường trung bình cho DHAE và giả thiết ABCD là hình vuông ta sẽ chứng minh được tứ giác BMNC là hình bình hành.c) Do AH ^ BN,   mà NM//CB Þ NM ^ AB nên M là trực tâm của tam giác ANB.d) M là trực tâm DABN nên BM ^ AN mà BM//CN Þ  $\widehat{ANC}$= 90⁰

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====