Câu hỏi:
Phân tích mỗi đa thức sau thành nhân tử:
a) x2 – 25 + 4xy + 4y2;
Trả lời:
a) x2 – 25 + 4xy + 4y2 = (x2 + 4xy + 4y2) – 25
= (x + 2y)2 – 52 = (x + 2y + 5)(x + 2y – 5);
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Làm thế nào để biến đổi được đa thức 3×2 – 5x dưới dạng tích của hai đa thức?
Câu hỏi:
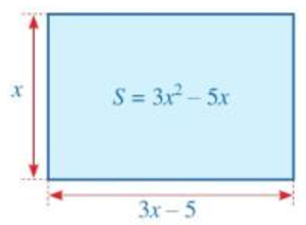
Làm thế nào để biến đổi được đa thức 3×2 – 5x dưới dạng tích của hai đa thức?
Trả lời:
Để biến đổi được đa thức 3×2 – 5x dưới dạng tích của hai đa thức, ta áp dụng tính chất phân phối của phép nhân đối với phép cộng.
Ta biến đổi như sau: 3×2 – 5x = x(3x – 5).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Viết đa thức 6×2 – 10x thành tích của hai đa thức bậc nhất.
Câu hỏi:
Viết đa thức 6×2 – 10x thành tích của hai đa thức bậc nhất.
Trả lời:
Đa thức 6×2 – 10x thành tích của hai đa thức bậc nhất như sau:
6×2 – 10x = 3x(x – 5).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Viết đa thức 6×2 – 10x thành tích của hai đa thức bậc nhất.
Câu hỏi:
Viết đa thức 6×2 – 10x thành tích của hai đa thức bậc nhất.
Trả lời:
Đa thức 6×2 – 10x thành tích của hai đa thức bậc nhất như sau:
6×2 – 10x = 3x(x – 5)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Viết mỗi đa thức sau dưới dạng tích của hai đa thức:
a) x2 – y2;
Câu hỏi:
Viết mỗi đa thức sau dưới dạng tích của hai đa thức:
a) x2 – y2;Trả lời:
a) x2 – y2 = (x + y)(x – y);
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- b) x3 – y3;
Câu hỏi:
b) x3 – y3;
Trả lời:
b) x3 – y3 = (x – y)(x2 + xy + y2);
====== **** mời các bạn xem câu tiếp bên dưới **** =====