Một chủ cửa hàng đã mua 100 cái điện thoại với giá  triệu đồng mỗi cái. Ông đã bán 75 cái với giá 6,2 triệu đồng một cái. Sau đó, ông giảm giá để bán hết số điện thoại còn lại. Vậy ông phải bán mỗi cái điện thoại còn lại với giá bao nhiêu để có lợi nhuận đạt tỉ lệ 20%?

Câu hỏi:

Một chủ cửa hàng đã mua 100 cái điện thoại với giá  triệu đồng mỗi cái. Ông đã bán 75 cái với giá 6,2 triệu đồng một cái. Sau đó, ông giảm giá để bán hết số điện thoại còn lại. Vậy ông phải bán mỗi cái điện thoại còn lại với giá bao nhiêu để có lợi nhuận đạt tỉ lệ 20%?

Trả lời:

Số tiền ông nhận được khi bán 75 cái điện thoại là: $6,2.75=465$ (triệu đồng)Số tiền ông nhận được nếu lợi nhuận đạt 20% là: $500.120\%=600$ (triệu đồng)Khi đó, số tiền ông nhận được khi bán 75 cái điện thoại là: $600-465=135$ (triệu đồng)Giá mỗi cái điện thoại là: $135:25=5,4$ (triệu đồng)

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Thực hiện các phép tính:a) 2x−32−4xx−3b) 15×3−10×2+x−2:x−2
   
   

   Câu hỏi:
   

   Thực hiện các phép tính:a) ${\left(2\mathrm{x}-3\right)}^2-4\mathrm{x}\left(\mathrm{x}-3\right)$b) $\left(15{\mathrm{x}}^3-10{\mathrm{x}}^2+\mathrm{x}-2\right):\left(\mathrm{x}-2\right)$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Phân tích các đa thức sau thành nhân tử:a) 3×2−12xy              b) x2+7x−2x+7c) 8×3−8×2+2x         d) x2−y2+12y−36
   
   

   Câu hỏi:
   

   Phân tích các đa thức sau thành nhân tử:a) $3{\mathrm{x}}^2-12\mathrm{xy}$              b) ${\mathrm{x}}^2+7\mathrm{x}-2\left(\mathrm{x}+7\right)$c) $8{\mathrm{x}}^3-8{\mathrm{x}}^2+2\mathrm{x}$         d) ${\mathrm{x}}^2-{\mathrm{y}}^2+12\mathrm{y}-36$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. a) Rút gọn phân thức: x3−36xx2+6x b) Thực hiện các phép tính, rút gọn: 2x−2+3x+2−18−5xx2−4
   
   

   Câu hỏi:
   

   a) Rút gọn phân thức: $\frac{{\mathrm{x}}^3-36\mathrm{x}}{{\mathrm{x}}^2+6\mathrm{x}}$ b) Thực hiện các phép tính, rút gọn: $\frac{2}{\mathrm{x}-2}+\frac{3}{\mathrm{x}+2}-\frac{18-5\mathrm{x}}{{\mathrm{x}}^2-4}$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Có 2 khu dân cư A và B cùng nằm bên bờ sông MN (như hình vẽ). Người ta muốn xây dựng một trạm cấp nước  trên bờ sông MN để cung cấp cho hai khu dân cư nói trên. Gọi C là địa điểm đặt trạm. Hãy xác định vị trí của C trên bờ sông MN để tổng độ dài đường ống dẫn nước từ đó tới hai khu dân cư A và B là ngắn nhất (giả thiết các đường ống dẫn nước là đường thẳng AC, BC).
   
   

   Câu hỏi:
   

   Có 2 khu dân cư A và B cùng nằm bên bờ sông MN (như hình vẽ). Người ta muốn xây dựng một trạm cấp nước  trên bờ sông MN để cung cấp cho hai khu dân cư nói trên. Gọi C là địa điểm đặt trạm. Hãy xác định vị trí của C trên bờ sông MN để tổng độ dài đường ống dẫn nước từ đó tới hai khu dân cư A và B là ngắn nhất (giả thiết các đường ống dẫn nước là đường thẳng AC, BC).

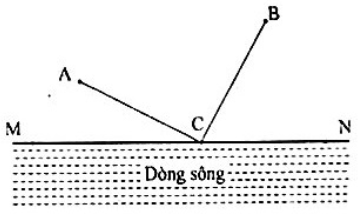
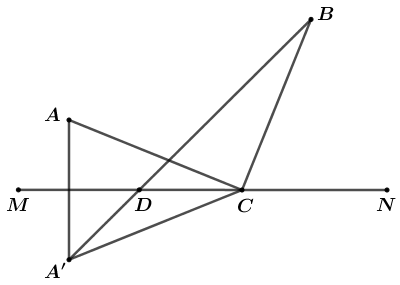
   Trả lời:

   Gọi A’ là điểm đối xứng với A qua MN và D là giao điểm của MN và BA’.Vì $\mathrm{C}\in \mathrm{MN}$ nên CA = CA’.Ta có: $\mathrm{CA}+\mathrm{CB}=\mathrm{CA}‘+\mathrm{CB}\le \mathrm{BA}‘$$\Rightarrow \mathrm{CA}‘+\mathrm{CB}\le \mathrm{DA}‘+\mathrm{BD}$.Dấu “=” xảy ra khi và chỉ khi $\mathrm{C}\equiv \mathrm{D}$.Vậy khi $\mathrm{C}\equiv \mathrm{D}$ thì tổng độ dài đường ống dẫn nước từ đó tới hai khu dân cư A và B là ngắn nhất.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình thang vuông ABCD AB //CD, A^=D^=90∘ có AD =  CD = 2AB. Gọi E là điểm đối xứng của A qua B.a) Chứng minh AE = 2AB và tứ giác AECD là hình vuông.b) Gọi M là trung điểm của EC và I là giao điểm của BC và DM. Chứng minh diện tích tam giác DIC bằng diện tích tứ giác EBIM.c) Biết DA và CB cắt nhau tại V. Gọi N là hình chiếu của I trên AD. Chứng minh NI2=ND.NV .
   
   

   Câu hỏi:
   

   Cho hình thang vuông ABCD $\left(\mathrm{AB}\text{\hspace{0.17em}//}\mathrm{CD},\hat{\mathrm{A}}=\hat{\mathrm{D}}={90}^{\circ }\right)$ có AD =  CD = 2AB. Gọi E là điểm đối xứng của A qua B.a) Chứng minh AE = 2AB và tứ giác AECD là hình vuông.b) Gọi M là trung điểm của EC và I là giao điểm của BC và DM. Chứng minh diện tích tam giác DIC bằng diện tích tứ giác EBIM.c) Biết DA và CB cắt nhau tại V. Gọi N là hình chiếu của I trên AD. Chứng minh ${\mathrm{NI}}^2=\mathrm{ND}.\mathrm{NV}$ .

   Trả lời:

   a) Chứng minh AE = 2AB và tứ giác AECD là hình vuông.Vì E là điểm đối xứng với A qua B nên B là trung điểm của AE. Do đó, AE = 2AB.Theo đề bài ta có: AD = CD = 2AB=> AD = CD = AE.Vì ABCD là hình thang vuông nên ta có: $\left\{\begin{array}{l}\mathrm{AB}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{CD}\\ \hat{\mathrm{A}}=\hat{\mathrm{D}}={90}^{\circ }\end{array}\right.$Xét tứ giác AECD ta có:AE // CDAE = CD=> Tứ giác AECD là hình bình hành (dấu hiệu nhận biết).Mà ta lại có: AD = AE (chứng minh trên)=> Tứ giác AECD là hình thoi (dấu hiệu nhận biết)Theo giả thiết: $\hat{\mathrm{A}}=\hat{\mathrm{D}}={90}^o$Suy ra, tứ giác AECD là hình vuông (dấu hiệu nhận biết)b) Gọi M là trung điểm của EC và I là giao điểm của BC và DM. Chứng minh diện tích tam giác DIC bằng diện tích tứ giác EBIM.Vì tứ giác AECD là hình vuông nên AE = CE = CD = DA (định nghĩa hình vuông)Vì M là trung điểm của EC nên EM = CM $=\frac{\mathrm{CE}}{2}$.Mà $\mathrm{BE}=\frac{\mathrm{AE}}{2}$ và AE = CE (chứng minh trên).=> BE = CMTa có: $\left.\begin{array}{l}{\mathrm{S}}_{\mathrm{BEC}}=\frac{1}{2}.\mathrm{BE}.\mathrm{CE}\\ {\mathrm{S}}_{\mathrm{DCM}}=\frac{1}{2}.\mathrm{CM}.\mathrm{DC}\end{array}\right\}\Rightarrow {\mathrm{S}}_{\mathrm{BEC}}={\mathrm{S}}_{\mathrm{DCM}}$$\Rightarrow {\mathrm{S}}_{\mathrm{BEMI}}+{\mathrm{S}}_{\mathrm{CMI}}={\mathrm{S}}_{\mathrm{DCI}}+{\mathrm{S}}_{\mathrm{CMI}}$$\Rightarrow {\mathrm{S}}_{\mathrm{BEMI}}={\mathrm{S}}_{\mathrm{DCI}}$ (đpcm)c) Biết DA và CB cắt nhau tại V. Gọi N là hình chiếu của I trên AD. Chứng minh ${\mathrm{NI}}^2=\mathrm{ND}.\mathrm{NV}$.Xét tam giác BEC và tam giác MCD ta có:BE = MC (cmt)$\widehat{\mathrm{BEC}}=\widehat{\mathrm{MCD}}={90}^{\circ }$EC = CE (cmt)$\Rightarrow \mathrm{\Delta BEC}=\mathrm{\Delta MCD}$ (c-g-c)$\Rightarrow \widehat{\mathrm{BCE}}=\widehat{\mathrm{MDC}}$ (hai góc tương ứng)Ta có: $\widehat{\mathrm{BCE}}+\overline{\mathrm{BCD}}={90}^{\circ }\Rightarrow \widehat{\mathrm{MDC}}+\widehat{\mathrm{BCD}}={90}^{\circ }$Xét tam giác DIC ta có: $\widehat{\mathrm{IDC}}+\widehat{\mathrm{DCI}}={90}^{\circ }\Rightarrow \widehat{\mathrm{DIC}}={90}^{\circ }$ (áp dụng định lý tổng ba góc trong một tam giác)=> DI vuông góc với BC tại I.Xét tam giác DNI vuông tại N, áp dụng định lý Py-ta-go ta có: ${\mathrm{ID}}^2={\mathrm{IN}}^2+{\mathrm{ND}}^2\Rightarrow {\mathrm{ND}}^2={\mathrm{ID}}^2-{\mathrm{IN}}^2$        Xét tam giác VNI vuông tại N, áp dụng định lý Py-ta-go ta có: ${\mathrm{IV}}^2={\mathrm{IN}}^2+{\mathrm{NV}}^2\Rightarrow {\mathrm{NV}}^2={\mathrm{IV}}^2-{\mathrm{IN}}^2$ Xét tam giác DVI vuông tại I, áp dụng định lý Py-ta-go ta có:${\mathrm{ID}}^2+{\mathrm{IV}}^2={\mathrm{DV}}^2$$\Rightarrow {\mathrm{ID}}^2+{\mathrm{IV}}^2={\left(\mathrm{VN}+\mathrm{ND}\right)}^2$$\Rightarrow {\mathrm{ID}}^2+{\mathrm{IV}}^2={\mathrm{VN}}^2+2\mathrm{VN}.\mathrm{ND}+{\mathrm{ND}}^2$$\Rightarrow {\mathrm{ID}}^2+{\mathrm{IV}}^2={\mathrm{IV}}^2-{\mathrm{IN}}^2+2\mathrm{VN}.\mathrm{ND}+{\mathrm{ID}}^2-{\mathrm{IN}}^2$$\Rightarrow 2{\mathrm{IN}}^2=2\mathrm{VN}.\mathrm{ND}$$\Rightarrow {\mathrm{IN}}^2=\mathrm{VN}.\mathrm{ND}$.Vậy ${\mathrm{NI}}^2=\mathrm{ND}.\mathrm{NV}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====