Câu hỏi:
Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.
Trả lời:
Gọi O là giao điểm của AB và IJ.
Vì ABCD là hình thang cân nên .
Xét ∆ABD và ∆BAC có:
AC = BD (chứng minh trên);
(chứng minh trên);
AD = BC (chứng minh trên).
Do đó ∆ABD = ∆BAC (c.g.c)
Suy ra (hai góc tương ứng).
Tam giác ICD cân tại I (vì ) nên IC = ID.
Vì nên .
Tam giác JCD cân tại J (vì ) nên JC = JD.
Xét ∆IJD và ∆IJC có:
IC = ID (chứng minh trên);
(chứng minh trên);
JC = JD (chứng minh trên).
Do đó ∆IJD = ∆IJC (c.g.c).
Suy ra (hai góc tương ứng).
Ta có ID = IC, AD = BC.
Mà ID = AI + AD; IC = IB + BC nên IA = IB.
Tam giác IAB cân tại I (vì IA = IB) có IO là tia phân giác
Suy ra IO là đường trung trực của đoạn thẳng AB.
Vậy đường thẳng IJ là đường trung trực của đoạn thẳng AB.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.
Câu hỏi:
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.
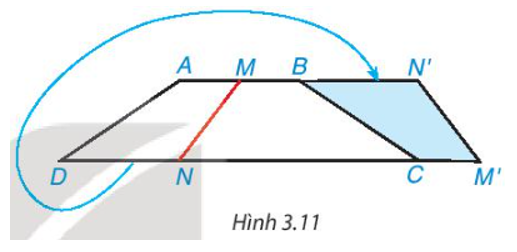
Trả lời:
Sau bài học này ta giải quyết được bài toán như sau:
Ta cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy.
Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu nên .
Tứ giác ABCD là hình thang cân nên AB // CD suy ra MN’ // M’N.
Do đó MN’M’N là hình thang.
Hình thang MN’M’N có nên MN’M’N là hình thang cân.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính các góc của hình thang cân ABCD (AB // CD), biết C^=40° (H.3.15).
Câu hỏi:
Tính các góc của hình thang cân ABCD (AB // CD), biết (H.3.15).
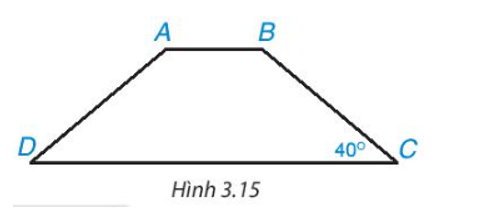
Trả lời:

====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình thang cân ABCD, AC // CD và AB < CD (H.3.16).
a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.
Câu hỏi:
Cho hình thang cân ABCD, AC // CD và AB < CD (H.3.16).
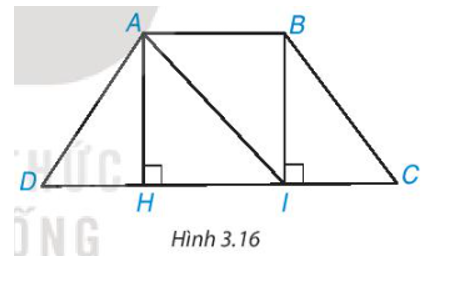
a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.Trả lời:
a) Vì ABCD là hình thang cân (AC // CD) nên (hai góc so le trong).
Ta có AH ⊥ DC, BI ⊥ DC suy ra AH // BI.
Do đó (hai góc so le trong).
Xét ∆AHI và ∆IBA có:
(chứng minh trên);
Cạnh AI chung;
(hai góc so le trong).
Do đó ∆AHI = ∆IBA (c.g.c).
Suy ra AH = BI (hai cạnh tương ứng).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC.
Câu hỏi:
b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC.
Trả lời:
b) Vì ABCD là hình thang cân (AC // CD) nên AD = BC; .
Xét ∆AHD và ∆BIC có:
(vì AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD);
AD = BC (chứng minh trên);
(chứng minh trên).
Do đó ∆AHD = ∆BIC (cạnh huyền – góc nhọn).
Suy ra AD = BC (hai cạnh tương ứng).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tứ giác ABCD như Hình 3.18. Biết rằng A^=B^=D^1. Chứng minh rằng AB = BC.
Câu hỏi:
Cho tứ giác ABCD như Hình 3.18. Biết rằng . Chứng minh rằng AB = BC.
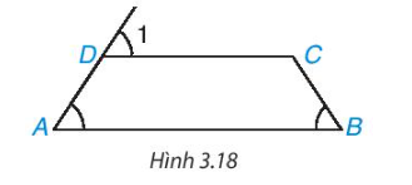
Trả lời:
Ta có mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có nên ABCD là hình thang cân.
Do đó AB = BC (đpcm).====== **** mời các bạn xem câu tiếp bên dưới **** =====