Hình chóp tứ giác có số các cạnh và mặt bên lần lượt là:

Câu hỏi:

Hình chóp tứ giác có số các cạnh và mặt bên lần lượt là:

A. 4 và 5

Đáp án chính xác

B. 8 và 4

C. 4 và 8

D. 8 và 5

Trả lời:

Chọn D

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Phần trắc nghiệm (3 điểm)Cho hình hộp chữ nhật ABCD.EFGH. Số các cặp mặt phẳng song song với nhau là:
   
   

   Câu hỏi:
   

   Phần trắc nghiệm (3 điểm)Cho hình hộp chữ nhật ABCD.EFGH. Số các cặp mặt phẳng song song với nhau là:

   A. 2

   B. 3

   Đáp án chính xác

   C. 4

   D. 5

   Trả lời:

   Chọn  B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình hộp chữ nhật ABCD.MNPQ có chiều dài AB = 22cm; chiều rộng BC = 14cm; chiều cao AM = 5cm. Thể tích hình hộp chữ nhật ABCD.MNPQ là:
   
   

   Câu hỏi:
   

   Cho hình hộp chữ nhật ABCD.MNPQ có chiều dài $AB = 22cm;$chiều rộng $BC = 14cm;$chiều cao $AM = 5cm.$ Thể tích hình hộp chữ nhật ABCD.MNPQ là:

   A. 1 540 $c{m}^3$

   Đáp án chính xác

   B. 770 $c{m}^3$

   C. 2 310 $c{m}^3$

   D. 180 $c{m}^3$

   Trả lời:

   Chọn A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Diện tích toàn phần của một hình lập phương là 726 cm2. Thể tích của hình lập phương này là:
   
   

   Câu hỏi:
   

   Diện tích toàn phần của một hình lập phương là $726 c{m}^2.$ Thể tích của hình lập phương này là:

   A. 1452 $c{m}^3$

   B. 2178 $c{m}^3$

   C. 1331 $c{m}^3$

   Đáp án chính xác

   D. 363 $c{m}^3$

   Trả lời:

   Chọn C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Một hình chóp tứ giác đều có thể tích bằng 96 cm3, chiều cao của hình chóp là 8cm. Độ dài cạnh đáy của hình chóp bằng:
   
   

   Câu hỏi:
   

   Một hình chóp tứ giác đều có thể tích bằng$96 c{m}^3,$chiều cao của hình chóp là 8cm. Độ dài cạnh đáy của hình chóp bằng:

   A. 6cm

   Đáp án chính xác

   B. 5cm 

   C. 7cm

   D. 8cm

   Trả lời:

   Chọn A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Phần tự luận (7 điểm)Cho hình hộp chữ nhật ABCD.EFGH. Chứng tỏ rằng:a) ACGE là hình chữ nhậtb) DF = CE
   
   

   Câu hỏi:
   

   Phần tự luận (7 điểm)Cho hình hộp chữ nhật ABCD.EFGH. Chứng tỏ rằng:a) ACGE là hình chữ nhậtb) DF = CE

   Trả lời:

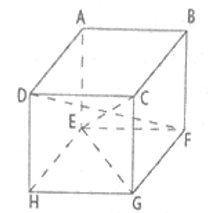   a) Ta có AE // CG; AE = CG (gt)Tứ giác ACGE là hình bình hànhMặt khác AE ⊥ mp(EFGH)Mà EG ⊂ mp(EFGH) => AE ⊥ EG tại EVậy tứ giác ACGE là hình chữ nhậtb) Chứng minh DF = CEVì DH ⊥ mp(EFGH ) nên DH ⊥ HF tại HSuy ra DF2 = DH2 + HF2(Py-ta-go)   (1)Vì AE ⊥ mp(ABCD) nên AE ⊥ AC tại ASuy ra CE2 = AE2 + AC2(Py-ta-go)   (2)Mà DH = AE; HF = EG = AC (hai đường chéo của hình chữ nhật)   (3)Từ (1), (2) và (3) suy ra DF2 = CE2 => DF = CE

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====