Câu hỏi:
Cho tam giác ABC. Vẽ đoạn thẳng MN. Hỏi rằng hai đường thẳng MN và BC có song song với nhau không? Vì sao?
Trả lời:
* Cách vẽ:- Kẻ tỉa Ax bất kì khác tia AB, AC- Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (đơn vị dài), EF = 3 (đơn vị dài)- Kẻ đường thẳng FB- Từ E kẻ đường thẳng song song với FB Cắt AB tại M.- Kẻ đường thẳng FC.- Từ E kẻ đường thẳng song song với FC cắt AC tại N.Ta có M, N là hai điểm cần vẽ.* Chứng minh:Trong ABC, ta có:Suy ra: MN // BC (Theo định lí đảo của định lí Ta-lét)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Giải SGK Toán 8 Ôn tập chương 3 Hình học
Giải bài tập Toán lớp 8 Ôn tập chương 3 Hình học
Trả lời câu hỏi giữa bài
Câu hỏi 1 trang 89 Toán 8 Tập 2: Phát biểu và viết tỉ lệ thức biểu thị hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thằng A’B’ và C’D’.
Trả lời:
Định nghĩa: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức:
hoặc
Câu hỏi 2 trang 89 Toán 8 Tập 2: Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta – let trong tam giác.
Trả lời:
Định lí Talet trong tam giác:
Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
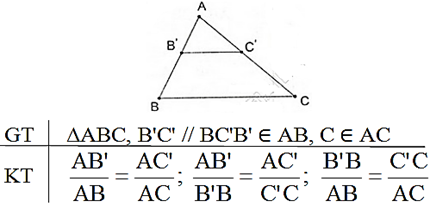
Câu hỏi 3 trang 89 Toán 8 Tập 2: Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta – let đảo.
Trả lời:
Định lí Talet đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
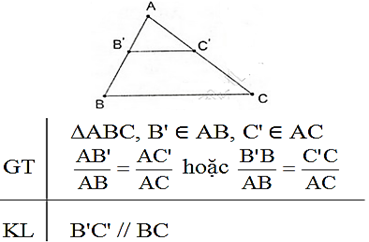
Câu hỏi 4 trang 89 Toán 8 Tập 2: Phát biểu, vẽ hình, ghi giả thiết và kết luận về hệ quả của định lí Ta – let.
Trả lời:
Hệ quả của định lí Talet:
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.
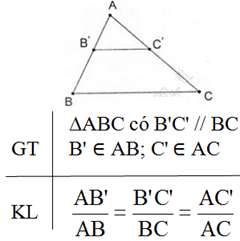
Câu hỏi 5 trang 89 Toán 8 Tập 2: Phát biểu định lí về tính chất của đường phân giác trong tam giác (vẽ hình, ghi giả thiết và kết luận).
Trả lời:
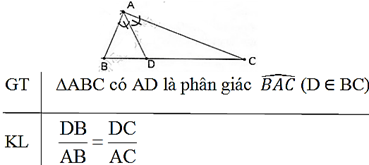
Định lý:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn ấy.
Câu hỏi 6 trang 89 Toán 8 Tập 2: Phát biểu định nghĩa hai tam giác đồng dạng.
Trả lời:
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
Câu hỏi 7 trang 89 Toán 8 Tập 2: Phát biểu định lí về đường thẳng song song với một cạnh của tam giác và cắt hai cạnh (hoặc phần kéo dài của hai cạnh) còn lại.
Trả lời:
Định lí:
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Câu hỏi 8 trang 89 Toán 8 Tập 2: Phát biểu định lí về ba trường hợp đồng dạng của hai tam giác.
Trả lời:
– Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
– Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
– Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Câu hỏi 9 trang 89 Toán 8 Tập 2: Phát biểu định lí về trường hợp đồng dạng đặc biệt của hai tam giác vuông (trường hợp cạnh huyền và một cạnh góc vuông).
Trả lời:
Định lí 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Bài tập (trang 92)
Bài 56 trang 92 Toán 8 Tập 2: Xác định tỉ số của hai đoạn thẳng AB và CD trong các trường hợp sau:
a) AB = 5cm, CD = 15cm;
b) AB = 45dm; CD = 150cm;
c) AB = 5CD.
Lời giải:
a) .
b) Đổi 45dm = 450 cm
Ta có: .
c) Vì AB = 5CD nên .
Bài 57 trang 92 Toán 8 Tập 2: Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M.
Lời giải:
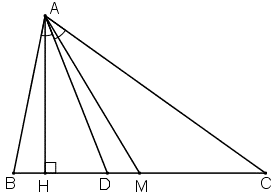
D luôn nằm giữa H và M.
– Ta chứng minh: D luôn nằm giữa H và M.
Vì AD là đường phân giác của tam giác ABC nên:
Mà AB < AC nên DB < DC
Suy ra: DB + DC < DC + DC
Hay BC < 2DC
Suy ra:
Mà M là trung điểm của BC nên
Suy ra: DC > MC nên M nằm giữa D và C (1).
Vì tam giác CAH vuông tại H nên:
Tổng ba góc của 1 tam giác bằng 1800 nên:
Suy ra:
Vì AB < AC nên
(trong 1 tam giác đối diện với cạnh lớn hơn thì góc đó lớn hơn).
Do đó:
Suy ra: tia AD nằm giữa hai tia AH và AC.
Suy ra: D nằm giữa H và C (2).
Từ (1) và (2) suy ra: D nằm giữa H và M.
Bài 58 trang 92 Toán 8 Tập 2: Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (h.66).
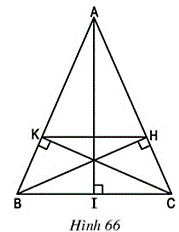
a) Chứng minh BK = CH.
b) Chứng minh KH // BC.
c) Cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng HK.
Hướng dẫn câu c):
– Vẽ thêm đường cao AI, xét hai tam giác đồng dạng IAC và HBC rồi tính CH.
– Tiếp theo, xét hai tam giác đồng dạng AKH và ABC rồi tính HK.
Lời giải:
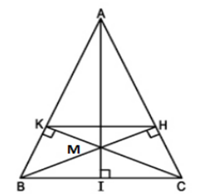
a) Xét tam giác BKC và tam giác CHB có:
BC chung
(vì tam giác ABC cân tại A)
Do đó, ∆BKC = ∆CHB (cạnh huyền – góc nhọn).
Suy ra: BK = CH.
b) Ta có: Tam giác ABC cân tại A nên AB = AC
Theo ý a ta có BK = CH
Suy ra: AK = AH (do AB = AC tam giác cân)
Do đó:
Suy ra: KH // BC (định lí Ta- let đảo).
c) Ta có: đường cao BH cắt đường cao CK tại M nên M là trực tâm tam giác ABC
Suy ra: AM vuông góc BC tại I.
Ta có: ∆AIC ∆ BHC ( vì
Mà HK // BC nên
Suy ra:
Bài 59 trang 92 Toán 8 Tập 2: Hình thang ABCD (AB // CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD.
Lời giải:
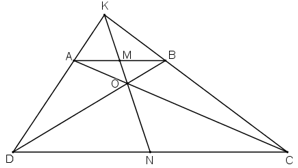
Gọi KO cắt AB, CD lần lượt tại M, N.
Xét ΔKDN có AM // DN (A ∈ KD, M ∈ KN)
⇒ (Hệ quả định lý Ta – let) (1)
Xét ΔKCN có BM // CN (M ∈ KN, B ∈ KC)
⇒ (Hệ quả định lý Ta – let) (2)
Từ (1); (2) suy ra:
Xét ΔOCN có AM // NC (A ∈ OC, M ∈ ON)
⇒ (Hệ quả định lý Ta – let)
Xét ΔODN có MB // ND (M ∈ ON, B ∈ OD)
⇒ (Hệ quả định lý Ta – let)
Suy ra:
Từ (3) và (4) suy ra
⇒ CN = DN
⇒ AM = MB
Vậy M, N là trung điểm AB, CD.
Bài 60 trang 92 Toán 8 Tập 2: Cho tam giác vuông ABC, = 90o, = 30o và đường phân giác BD (D thuộc cạnh AC).
a) Tính tỉ số .
b) Cho biết độ dài AB = 12,5cm. Hãy tính chu vi và diện tích của tam giác ABC.
Lời giải:
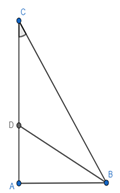
a)
+ Xét Δ ABC vuông tại A, có
(Trong một tam giác vuông, cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
+ Xét ΔABC có BD là phân giác của
(tính chất đường phân giác)
Mà nên .
Suy ra: .
b) AB = 12,5cm ⇒ BC = 2AB = 2.12,5 = 25cm
Áp dụng định lí Py- ta- go vào tam giác ABC ta có:
AB2 + AC2 = BC2 nên AC2 = BC2 – AB2
+ Chu vi tam giác ABC là:
P = AB + BC + CA
+ Diện tích tam giác ABC là:
Bài 61 trang 92 Toán 8 Tập 2: Tứ giác ABCD có AB = 4cm, BC = 20cm, CD = 25cm. DA = 8cm, đường chéo BD = 10cm.
a) Nêu cách vẽ tứ giác ABCD có kích thước đã cho ở trên.
b) Các tam giác ABD và BDC có đồng dạng với nhau không? Vì sao?
c) Chứng minh rằng AB // CD.
Lời giải:
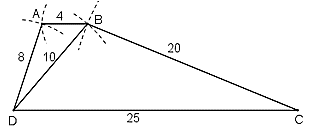
a) Cách vẽ:
– Vẽ ΔBDC:
+ Vẽ DC = 25cm
+ Vẽ cung tròn tâm D có bán kính = 10cm và cung tròn tâm C có bán kính = 20cm. Giao điểm của hai cung tròn là điểm B.
Nối DB và BC.
– Vẽ điểm A: Vẽ cung tròn tâm B có bán kính = 4cm và cung tròn tâm D có bán kính = 8cm. Giao điểm của hai cung tròn này là điểm A.
Nối DA và BA.
Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.
b) Ta có:
Suy ra: ∆ABD ∆BDC (c.c.c)
c) Vì ∆ABD ∆BDC nên (hai góc tương ứng)
Mà 2 góc này ở vị trí so le trong nên AB // DC
Dó đó: ABCD là hình thang.
- Giải SGK Toán 8 Ôn tập chương 3 Đại số
Giải bài tập Toán lớp 8 Ôn tập chương 3 Đại số
Trả lời câu hỏi giữa bài
Câu hỏi 1 trang 32 Toán 8 Tập 2: Thế nào là hai phương trình tương đương?
Trả lời:
Hai phương trình tương đương là hai phương trình có cùng một tập nghiệm.
Câu hỏi 2 trang 32 Toán 8 Tập 2: Nhân hai vế của một phương trình với cùng một biểu thức chứa ẩn thì có thể không được phương trình tương đương. Em hãy cho một ví dụ.
Trả lời:
Ví dụ: phương trình (1) x – 1 = 3 có tập nghiệm S1 = {4}.
Nhân hai vế của phương trình (1) với x, ta được phương trình:
(x – 1)x = 3x (2)
⇔ (x – 1)x – 3x = 0
⇔ x(x – 4) = 0
Suy ra: x = 0 hoặc x – 4 = 0
Nếu x – 4 = 0 thì x = 4.
Phương trình (2) có tập nghiệm là S2 = {0, 4}.
Vì S1 ≠ S2 nên hai phương trình (1) và (2) không tương đương.
Câu hỏi 3 trang 32 Toán 8 Tập 2: Với điều kiện nào của a thì phương trình ax + b = 0 là một phương trình bậc nhất? (a và b là hai hằng số).
Trả lời:
Với điều kiện a ≠ 0 thì phương trình ax + b = 0 là một phương trình bậc nhất.
Câu hỏi 4 trang 32 Toán 8 Tập 2: Một phương trình bậc nhất một ẩn có mấy nghiệm? Đánh dấu “x” vào ô vuông ứng với câu trả lời đúng:
Vô nghiệm
Luôn có nghiệm
Có vô số nghiệm
Có thể vô nghiệm, có thể có một nghiệm duy nhất và cũng có thể có vô số nghiệm
Trả lời:
Ô vuông thứ 2: Một phương trình bậc nhất một ẩn luôn có một nghiệm duy nhất.
Chú ý vì đây là phương trình bậc nhất một ẩn nên a ≠ 0, do đó phương trình luôn có một nghiệm duy nhất. Không có trường hợp a = 0.
Câu hỏi 5 trang 33 Toán 8 Tập 2: Khi giải phương trình chứa ẩn ở mẫu, ta phải chú ý điều gì?
Trả lời:
Khi giải phương trình chứa ẩn ở mẫu, ta phải chú ý đến điều kiện xác định của phương trình.
Câu hỏi 6 trang 33 Toán 8 Tập 2: Hãy nêu các bước giải bài toán bằng cách lập phương trình.
Trả lời:
Bước 1. Lập phương trình.
– Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số;
– Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;
– Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình.
Bước 3. Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không thỏa mãn, rồi kết luận.
Bài tập (trang 33; 34)
Bài 50 trang 33 Toán 8 Tập 2: Giải các phương trình:
a) 3 – 4x(25 – 2x) = 8x2 + x – 300.
b) ;
c) ;
d) .
Lời giải:
a) 3 – 4x(25 – 2x) = 8x2 + x – 300
⇔ 3 – 4x.25 + 4x.2x = 8x2 + x – 300
⇔ 3 – 100x + 8x2 = 8x2 + x – 300
⇔ -101x = -303
⇔ x = 3.
Vậy phương trình có tập nghiệm S = {3}.
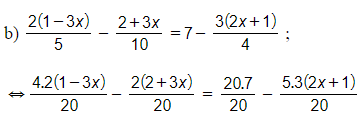
⇔ 8(1- 3x) – 2(2 + 3x) = 140 – 15(2x + 1)
⇔ 8 – 24x – 4 – 6x = 140 – 30x – 15
⇔ -24x – 6x + 30x = 140 – 15 – 8 + 4
⇔ 0x = 121 (vô lý)
Vậy phương trình vô nghiệm.
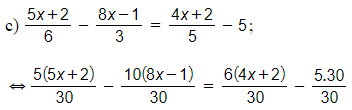
⇔ 5(5x + 2) – 10(8x – 1) = 6(4x + 2) – 150
⇔ 25x + 10 – 80x + 10 = 24x + 12 – 150
⇔ 20 – 55x = 24x – 138
⇔ -55x – 24x = -138 – 20
⇔ -79x = -158
⇔ x = 2.
Vậy phương trình có tập nghiệm S = {2}.
d)
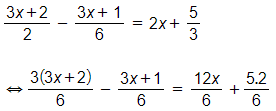
⇔ 3(3x + 2) – (3x + 1) = 12x + 10
⇔ 9x + 6 – 3x – 1 = 12x + 10
⇔ 6x + 5 = 12x + 10
⇔ 6x – 12x = 10 – 5
⇔ -6x = 5
⇔
Vậy phương trình có tập nghiệm .
Bài 51 trang 33 Toán 8 Tập 2: Giải các phương trình sau bằng cách đưa về phương trình tích:
a) (2x + 1)(3x – 2) = (5x – 8)(2x + 1);
b) 4x2 – 1 = (2x + 1)(3x – 5);
c) (x + 1)2 = 4(x2 – 2x + 1);
d) 2x3 + 5x2 – 3x = 0.
Lời giải:
a) (2x + 1)(3x – 2) = (5x – 8)(2x + 1)
⇔ (2x + 1)(3x – 2) – (5x – 8)(2x + 1) = 0
⇔ (2x + 1).[(3x – 2) – (5x – 8)] = 0
⇔ (2x + 1).(3x – 2 – 5x + 8) = 0
⇔ (2x + 1)(6 – 2x) = 0
⇔ 2x + 1 = 0 hoặc 6 – 2x = 0
Nếu 2x + 1 = 0 ⇔ 2x = -1 ⇔ x = .
Nếu 6 – 2x = 0 ⇔ 6 = 2x ⇔ x = 3.
Vậy phương trình có tập nghiệm .
b) 4x2 – 1 = (2x + 1)(3x – 5)
⇔ 4x2 – 1 – (2x + 1)(3x – 5) = 0
⇔ (2x – 1)(2x + 1) – (2x + 1)(3x – 5) = 0
⇔ (2x + 1)[(2x – 1) – (3x – 5)] = 0
⇔ (2x + 1)(2x – 1 – 3x + 5) = 0
⇔ (2x + 1)(4 – x) = 0
⇔ 2x + 1= 0 hoặc 4 – x = 0
Nếu 2x + 1 = 0 ⇔ 2x = -1 ⇔ .
Nếu 4 – x = 0 ⇔ x = 4.
Vậy phương trình có tập nghiệm .
c)
Cách 1:
(x + 1)2 = 4(x2 – 2x + 1)
⇔ (x + 1)2 – 4(x2 – 2x + 1) = 0
⇔ (x + 1)2 – 22. (x -1)2 = 0
⇔ (x + 1)2 – [ 2(x – 1)]2 =0
⇔ [(x + 1) + 2( x – 1)].[(x + 1) – 2( x – 1)]= 0
⇔ ( x + 1 + 2x – 2)(x + 1 – 2x + 2) =0
⇔ (3x – 1)(3 – x) = 0
⇔ 3x – 1 = 0 hoặc 3 – x = 0
Nếu 3x – 1 = 0 ⇔ 3x = 1 ⇔ .
Nếu 3 – x = 0 ⇔ x = 3
Vậy tập nghiệm của phương trình đã cho là: .
* Cách 2: Ta có:
(x + 1)2 = 4(x2 – 2x + 1)
⇔ (x + 1)2 – 4(x2 – 2x + 1) = 0
⇔ x2 + 2x +1 – 4x2 + 8x – 4 = 0
⇔ -3x2 + 10x – 3 = 0
⇔ (-3x2 + 9x) + (x – 3) = 0
⇔ -3x(x – 3) + ( x – 3) = 0
⇔ ( x- 3).(-3x + 1) = 0
⇔ x – 3 = 0 hoặc -3x + 1= 0
Nếu x – 3 = 0 x = 3
Nếu – 3x + 1 = 0 hay – 3x = – 1 ⇔
Vậy tập nghiệm của phương trình đã cho là: .
d) 2x3 + 5x2 – 3x = 0
⇔ x(2x2 + 5x – 3) = 0
⇔ x.(2x2 + 6x – x – 3) = 0
⇔ x. [2x(x + 3) – (x + 3)] = 0
⇔ x.(2x – 1)(x + 3) = 0
⇔ x = 0 hoặc 2x – 1 = 0 hoặc x + 3 = 0
Nếu 2x – 1 = 0 ⇔ 2x = 1 ⇔ .
Nếu x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm .
Bài 52 trang 33 Toán 8 Tập 2: Giải các phương trình:
![Giải các phương trình [1/(2x - 3)] - [ 3/ x(2x-3) ] = 5/x (ảnh 1)](https://hoc.io.vn/wp-content/uploads/2023/10/screenshot-1643075675-1643075687.png)
Lời giải:
a) Điều kiện xác định: x ≠ 0 và x ≠ .
Suy ra: x – 3 = 5(2x – 3)
⇔ x – 3 = 10x – 15
⇔ x – 10x = -15 + 3
⇔ -9x = -12
⇔ . ( thỏa mãn điều kiện).
Vậy phương trình có tập nghiệm .
b) Điều kiện xác định: x ≠ 0; x ≠ 2.
⇒ x(x + 2) – (x – 2) = 2
⇔ x2 + 2x – x + 2 = 2
⇔ x2 + x = 0
⇔ x(x + 1) = 0
⇔ x = 0 hoặc x + 1 = 0.
Nếu x = 0 không thỏa mãn điều kiện xác định.
Nếu x + 1 = 0 ⇔ x = -1 (thỏa mãn điều kiện xác định).
Vậy phương trình có tập nghiệm S = {-1}.
c) Điều kiện xác định: x ≠ ±2.
![Giải các phương trình [1/(2x - 3)] - [ 3/ x(2x-3) ] = 5/x (ảnh 1)](https://hoc.io.vn/wp-content/uploads/2023/10/screenshot-1643075578-1643075590.png)
⇒ (x + 1)(x + 2) + (x – 1)(x – 2) = 2(x2 + 2)
⇔ x2 + x + 2x + 2 + x2 – x – 2x + 2 = 2x2 + 4
⇔ 2x2 + 4 = 2x2 + 4
⇔ 0x = 0 luôn đúng với mọi x thỏa mãn điều kiện.
Vậy phương trình nghiệm đúng với mọi x ≠ ±2.
d) Điều kiện xác định: x ≠ .
![Giải các phương trình [1/(2x - 3)] - [ 3/ x(2x-3) ] = 5/x (ảnh 1)](https://hoc.io.vn/wp-content/uploads/2023/10/screenshot-1643075536-1643075560.png)
+ Nếu
(thỏa mãn điều kiện).
+ Nếu x + 8 = 0 thì x = -8 (thỏa mãn điều kiện).
Vậy phương trình có tập nghiệm là .
Bài 53 trang 34 Toán 8 Tập 2: Giải phương trình:
Lời giải:
Ta có:
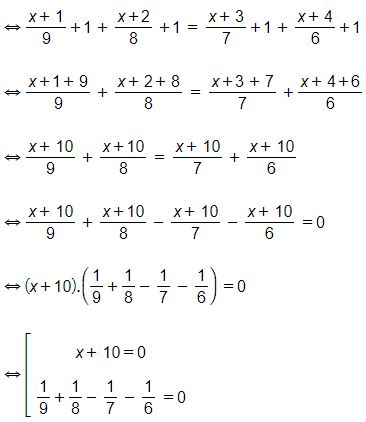
Nếu x + 10 = 0 thì x= -10
Vì
Vậy phương trình có nghiệm duy nhất là x = -10.
Bài 54 trang 34 Toán 8 Tập 2: Một canô xuôi dòng từ bến A đến bến B mất 4 giờ và ngược dòng từ bến B về bến A mất 5 giờ. Tính khoảng cách giữa hai bến A và B, biết rằng vận tốc của dòng nước là 2 km/h.
Lời giải:
Gọi x (km) là khoảng cách giữa hai bến A và B, với x > 0.
Vì canô xuôi dòng mất 4h nên vận tốc canô khi xuôi dòng là: (km/h)
Vì canô ngược dòng mất 5h nên vận tốc canô khi ngược dòng là (km/h).
Vận tốc dòng nước là 2km/h.
Vì khi đi xuôi dòng thì vận tốc xuôi dòng sẽ gồm vận tốc canô cộng vận tốc nước, và đi ngược dòng thì vận tốc canô bằng vận tốc thực trừ vận tốc nước nên vận tốc xuôi dòng lớn hơn vận tốc ngược dòng chính bằng 2 lần vận tốc dòng nước. Do đó ta có phương trình:
Suy ra: x = 80 (thỏa mãn điều kiện).
Vậy khoảng cách giữa hai bến A và B là 80 km.
(Giải thích: hiệu vận tốc xuôi dòng và ngược dòng bằng 2 lần vận tốc dòng nước:
Nếu gọi vận tốc canô là v (km/h), vận tốc dòng nước là a (km/h), ta có:
Khi xuôi dòng: vận tốc canô = v + a
Khi ngược dòng: vận tốc canô = v – a
Hiệu vận tốc = v + a – (v – a) = 2a = 2.vận tốc dòng nước.)
Bài 55 trang 34 Toán 8 Tập 2: Biết rằng 200g một dung dịch chứa 50g muối. Hỏi phải pha thêm bao nhiêu gam nước vào dung dịch đó để được một dung dịch chứa 20% muối?
Lời giải:
Gọi x (g) là khối lượng nước phải pha thêm, với x > 0.
Khối lượng dung dịch mới: 200 + x (g)
Ta có: nồng độ dung dịch = số g muối / số g dung dịch.
Vì khối lượng muối không đổi nên nồng độ dung dịch sau khi pha thêm nước bằng
Theo đề bài, nồng độ dung dịch mới chứa 20% muối nên ta có phương trình:
Suy ra: 250 = 200 + x
(thỏa mãn điều kiện).
Vậy phải pha thêm 50g nước để được dung dịch chứa 20% muối.
Bài 56 trang 34 Toán 8 Tập 2: Để khuyến khích tiết kiệm điện, giá điện sinh hoạt được tính theo kiểu lũy tiến, nghĩa là nếu người sử dụng càng nhiều điện thì giá mỗi số điện (1kw/h) càng tăng lên theo các mức như sau:
Mức thứ nhất: Tính cho 100 số điện đầu tiên;
Mức thứ hai: Tính cho số điện thứ 101 đến 150, mỗi số đắt hơn 150 đồng so với mức thứ nhất;
Mức thứ ba: Tính cho số điện thứ 151 đến 200, mỗi số đắt hơn 200 đồng so với mức thứ hai;
v.v…
Ngoài ra người sử dụng còn phải trả thêm 10% thuế giá trị gia tăng (thuế VAT).
Tháng vừa qua, nhà Cường dùng hết 165 số điện và phải trả 95700 đồng. Hỏi mỗi số điện ở mức thứ nhất giá là bao nhiêu?
Lời giải:
Gọi x (đồng) là giá mỗi số điện ở mức thứ nhất (x > 0).
⇒ Giá mỗi số điện ở mức 2 là: x + 150 (đồng)
⇒ Giá mỗi số điện ở mức 3 là: x + 150 + 200 = x + 350 (đồng)
Nhà Cường dùng hết 165 số điện = 100 + 50 + 15.
Như vậy nhà Cường phải đóng cho 100 số điện ở mức 1, 50 số điện ở mức 2 và 15 số điện ở mức 3.
Giá tiền 100 số điện mức đầu tiên là: 100.x (đồng)
Giá tiền 50 số điện mức thứ hai là: 50.(x + 150) (đồng)
Giá tiền 15 số điện còn lại mức thứ ba là: 15.(x + 350) (đồng).
⇒ Số tiền điện (chưa tính VAT) của nhà Cường bằng:
100.x + 50.(x + 150) + 15.(x + 350)
= 100x + 50x + 50.150 +15x +15.350
= 165x + 12750.
Thuế VAT nhà Cường phải trả là:
(165x + 12750).10%
Tổng số tiền điện nhà Cường phải đóng (tiền gốc + thuế) bằng:
165x + 12750 + 0,1.(165x + 12750) = 1,1.(165x + 12750).
Thực tế nhà Cường hết 95700 đồng nên ta có phương trình:
1,1(165x + 12750) = 95700
⇔ 165x + 12750 = 87000
⇔ 165x = 74250
⇔ x = 450 (đồng) (thỏa mãn điều kiện).
Vậy mỗi số điện ở mức giá đầu tiên là 450 đồng.
- Lý thuyết Toán lớp 6 Chương 3 (Cánh diều 2023): Hình học trực quan hay, chi tiết
Lý thuyết Toán lớp 6 Chương 3: Hình học trực quan
A. Lý thuyết Chương 3: Hình học trực quan
1. Tam giác đều
1.1 Nhận biết tam giác đều
Tam giác đều ABC có
+ Ba cạnh bằng nhau: AB = BC = CA
+ Ba góc ở các đỉnh A, B, C bằng nhau.
Chú ý: Trong hình học nói chung, tam giác nói riêng, các cạnh bằng nhau (hay các góc bằng nhau) thường được chỉ rõ ràng bằng cùng một ký hiệu (xem hình vẽ trên).
1.2 Vẽ tam giác đều
Vẽ tam giác đều bằng thước và compa khi biết độ dài cạnh.
Ví dụ: Dùng thước và compa vẽ tam giác đều ABC có độ dài cạnh bằng 3 cm.
Lời giải:
Để vẽ tam giác đều ABC có độ dài cạnh bằng 3 cm, ta làm như sau:
Bước 1. Dùng thước vẽ đoạn thẳng AB = 3 cm
Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.
Bước 3. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.
Bước 4. Dùng thước vẽ các đoạn thẳng AC và BC
Khi đó ta được tam giác đều ABC có cạnh bằng 3 cm.
2. Hình vuông
2.1 Nhận biết hình vuông
Hình vuông ABCD có:
+ Bốn cạnh bằng nhau: AB = BC = CD = DA
+ Hai cạnh đối AB và CD; AD và BC song song với nhau.
+ Hai đường chéo bằng nhau: AC = BD
+ Bốn góc ở các đỉnh A, B, C, D là góc vuông.
2.2 Vẽ hình vuông
Dùng ê ke vẽ hình vuông khi biết độ dài cạnh.
Ví dụ: Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh bằng 7 cm.
Lời giải:
Để vẽ hình vuông ABCD, ta làm như sau:
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB = 7 cm.
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke bằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD = 7cm.
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC = 7 cm.
Bước 4. Vẽ đoạn thẳng CD.
2.3 Chu vi và diện tích của hình vuông
Hình vuông có độ dài cạnh bằng a có:
+ Chu vi của hình vuông là C = 4a
+ Diện tích của hình vuông là S = a . a = a2
3. Lục giác đều
Lục giác đều ABCDEF có:
+ Sáu cạnh bằng nhau: AB = BC = CD = DE = EF = FA
+ Ba đường chéo chính cắt nhau tại điểm O.
Ba đường chéo chính bằng nhau: AD = BE = CF
+ Sáu góc ở các đỉnh A, B, C, D, E, F bằng nhau.
4. Hình chữ nhật
4.1 Nhận biết hình chữ nhật
Cho hình chữ nhật ABCD:
Khi đó hình chữ nhật ABCD có:
+ Hai cạnh đối bằng nhau: AB = CD; AD = BC;
+ Hai cạnh đối AB và CD; AD và BC song song với nhau;
+ Hai đường chéo bằng nhau: AC = BD;
+ Bốn góc ở các đỉnh A, B, C, D đều là góc vuông.
4.2 Vẽ hình chữ nhật
Ta sử dụng ê ke để vẽ hình chữ nhật khi biết độ dài hai cạnh của nó:
Chẳng hạn, vẽ hình chữ nhật ABCD biết AB = 6 cm, AD = 9 cm.
Ta thực hiện các bước như sau:
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB = 6 cm.
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD = 9 cm.
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC = 9 cm.
Bước 4. Vẽ đoạn thẳng CD.
Vậy ta có hình chữ nhật ABCD thỏa mãn yêu cầu bài toán.
4.3 Chu vi và diện tích hình chữ nhật
Hình chữ có độ dài hai cạnh là a và b, ta có:
– Chu vi của hình chữ nhật là: C = 2(a + b);
– Diện tích của hình chữ nhật là: S = a . b.
5. Hình thoi
5.1 Nhận biết hình thoi
Cho hình thoi ABCD, có hai đường chéo AC và BD cắt nhau tại O.
Khi đó, hình thoi ABCD có:
+ Bốn cạnh bằng nhau: AB = BC = CD = DA;
+ Hai cạnh đối AB và CD, AD và BC song song với nhau;
+ Hai đường chéo AC và BD vuông góc với nhau.
5.2 Vẽ hình thoi
Ta có thể vẽ được hình thoi khi biết độ dài một cạnh và độ dài một đường chéo bằng thước kẻ và compa.
Chẳng hạn, vẽ hình thoi ABCD biết AB = 5 cm và AC = 8 cm.
Để vẽ hình thoi ABCD, ta làm như sau:
Bước 1. Dùng thước vẽ đoạn thẳng AC = 8 cm
Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính 5 cm
Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính 5 cm; phần đường tròn này cắt phần đường tròn tâm A vẽ ở Bước 2 tại các điểm B và D
Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA.
Vậy ta được hình thoi ABCD thỏa mãn yêu cầu.
5.3 Chu vi và diện tích hình thoi
Cho hình thoi có độ dài cạnh là a và độ dài hai đường chéo là m và n, ta có:
– Chu vi của hình thoi là C = 4a;
– Diện tích của hình thoi là S = . m . n.
6. Hình bình hành
6.1 Nhận biết hình bình hành
Cho hình bình hành ABCD
Khi đó hình bình hành ABCD có:
+ Hai cạnh đối AB và CD, BC và AD song song với nhau;
+ Hai cạnh đối bằng nhau: AB = CD; BC = AD;
+ Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.
6.2 Vẽ hình bình hành
Ta có thể vẽ hình bình hành bằng thước và compa.
Chẳng hạn, vẽ hình bình hành ABCD nhận hai đoạn thẳng AB, AD làm cạnh.
Để vẽ hình bình hành ABCD ta thực hiện các bước sau:
Bước 1. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AD. Lấy D làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi C là giao điểm của hai phần đường tròn này.
Bước 2. Dùng thước vẽ các đoạn thẳng BC và CD.
Ta được hình bình hành ABCD.
6.3 Chu vi và diện tích của hình bình hành
Hình bình hành có độ dài hai cạnh là a và b, độ dài đường cao ứng với cạnh a là h, ta có:
– Chu vi của hình bình hành là C = 2(a + b);
– Diện tích của hình bình hành là S = a . h.
7. Hình thang cân
7.1 Nhận biết hình thang cân
Cho hình thang cân ABCD
Khi đó hình thang cân ABCD có:
+ Hai cạnh đáy AB và CD song song với nhau;
+ Hai cạnh bên bằng nhau: AD = BC; hai đường chéo bằng nhau: AC = BD;
+ Hai góc kề với đáy AB bằng nhau, tức là hai góc DAB và CBA bằng nhau; hai góc kề với đáy CD bằng nhau, tức là hai góc ADC và góc BCD bằng nhau.
7.2 Chu vi và diện tích hình thang cân
(Hình thang cân có hai cạnh bên bằng nhau)
– Chu vi của hình thang cân bằng tổng độ dài các cạnh của hình thang cân đó
C = a + b + c + c = a + b + 2c
– Diện tích của hình thang cân bằng tổng độ dài hai cạnh đáy nhân với chiều cao rồi chia đôi
.
8. Hình có trục đối xứng
Quan sát các hình sau:
Các hình trên có đặc điểm chung là khi chia mỗi hình thành hai nửa và gấp theo mép đường thẳng ở giữa hình thì hai nửa này sẽ trùng khít vào nhau.
Cụ thể, trong hình dưới đây:
Đường thẳng d chia hình thành hai nửa, nếu ta gấp theo đường thẳng d thì hai nửa này sẽ trùng khít vào nhau.
Những hình như vậy gọi là hình có trục đối xứng và đường thẳng d được gọi là trục đối xứng của hình.
Chú ý: Hình có trục đối xứng còn được gọi là hình đối xứng trục.
9. Trục đối xứng của một số hình
9.1 Đoạn thẳng AB là hình có trục đối xứng và trục đối xứng là đường thẳng d đi qua trung điểm O của đoạn thẳng AB và vuông góc với AB.
9.2 Đường tròn là hình có nhiều trục đối xứng và mỗi trục đối xứng là một đường thẳng đi qua tâm của nó.
9.3 Hình thang cân có một trục đối xứng là đường thẳng a đi qua điểm chính giữa của hai đáy.
9.4 Hình lục giác đều có 6 trục đối xứng là các đường thẳng m, n, p, q, r, s (như hình dưới
Chú ý: Không phải hình nào cũng đều có trục đối xứng.
10. Hình có tâm đối xứng
10.1 Cho đường tròn tâm O, đường kính AB.
+ Vì O là trung điểm của đoạn thẳng AB nên ta nói hai điểm A và B đối xứng với nhau qua tâm O.
+ Đường tròn tâm O là hình có tâm đối xứng, tâm đối xứng chính là tâm O của đường tròn.
10.2 Lấy bốn chiếc ê ke giống nhau để xếp thành hình. Ta được một hình mới là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Chú ý: Hình có tâm đối xứng còn được gọi là hình đối xứng tâm.
11. Tâm đối xứng của một số hình
11.1 Đoạn thẳng MN là hình có tâm đối xứng và tâm đối xứng là trung điểm I của đoạn thẳng đó.
11.2 Hình tròn là hình có tâm đối xứng và tâm đối xứng là tâm của nó.
11.3 Hình thoi, hình vuông, hình chữ nhật, hình lục giác đều có tâm đối xứng là giao điểm của các đường chéo.
12. Tính đối xứng trong thế giới tự nhiên
+ Tính đối xứng là sự giống nhau của một hình qua đường trục hoặc qua tâm, tạo nên sự cân bằng.
+ Trong tự nhiên, tính đối xứng được thể hiện rất đa dạng, phong phú, chẳng hạn: con bướm, cầu vồng, sao biển,…
+ Tính đối xứng của một đối tượng là một trong những dấu hiệu quan trọng nhất giúp chúng ta nhanh chóng định hình đối tượng đó khi nhìn vào nó. Ngoài ra, với con người, đối xứng tạo ra sự cân bằng, hài hòa, trật tự nhờ đó tạo ra thẩm mĩ.
13. Tính đối xứng trong nghệ thuật, kiến trúc và công nghệ
Nguyên tắc cân bằng là một trong những nguyên tắc quan trọng với nghệ thuật hay kiến trúc.
Bố cục đối xứng thường được sử dụng trong các tác phẩm nghệ thuật hay kiến trúc.
Một số ví dụ:
Trong thiết kế, công nghệ, chúng ta cũng dễ dàng nhận ra các bố cục có tính đối xứng.
Các công trình hay máy móc muốn tồn tại, ổn định, bền vững và có được vẻ đẹp, bắt mắt thì phải chú trọng đến tính cân xứng.
Một số ví dụ:
B. Bài tập tự luyện
Bài 1. Một mảnh vườn có dạng hình vuông với chiều dài cạnh bằng 25 m. Người ta để một phần của mảnh vườn làm lối đi rộng 2 m như Hình dưới, phần còn lại để trồng rau.
a) Tính diện tích phần vườn trồng rau.
b) Người ta làm hàng rào xung quanh mảnh vườn trồng rau và ở một góc vườn rau có để cửa ra vào rộng 2m. Tính độ dài của hàng rào đó.
Lời giải:
a) Vì người ta để một phần của mảnh vườn làm lối đi rộng 2 m nên phần vườn trồng rau là mảnh đất hình vuông và có độ dài cạnh là:
25 – 2 = 23 (m)
Diện tích phần vườn trồng rau là:
23 . 23 = 529 (m2)
b) Chu vi của phần vườn trồng rau hình vuông là:
4 . 23 = 92 (m)
Độ dài của hàng rào chính là chu vi của phần vườn trồng rau trừ đi phần cửa ra vào rộng 2 m. Do đó độ dài của hàng rào là:
92 – 2 = 90 (m)
Vậy diện tích của phần vườn trồng rau là 529 m2, độ dài của hàng rào là 90 m.
Bài 2. Bác Hưng uốn một dây thép thành móc treo đồ có dạng hình thoi với độ dài cạnh bằng 30 cm. Bác Hưng cần bao nhiêu xăng-ti-mét dây thép để làm móc treo đó?
Lời giải:
Độ dài dây thép để làm móc treo chính là chu vi của hình thoi có độ dài cạnh bằng 30 cm.
Do đó bác Hưng cần số xăng-ti-mét dây thép để làm móc treo là:
4 . 30 = 120 (cm)
Vậy bác Hưng cần số xăng-ti-mét dây thép để làm móc treo là 120 cm.
Bài 3. Vẽ hai đoạn thẳng MN và MQ. Từ đó, vẽ hình bình hành MNPQ nhận hai đoạn thẳng MN và MQ làm cạnh.
Lời giải:
Ta lần lượt thực hiện qua các bước sau:
Bước 1. Lấy điểm M bất kì, vẽ hai đoạn thẳng MN, MQ sao cho MN và MQ không trùng lên nhau và có độ dài khác nhau như hình dưới đây.
Bước 2. Lấy Q làm tâm, dùng compa vẽ một phần đường tròn có bán kính MN. Lấy N làm tâm, dùng compa vẽ một phần đường tròn có bán kính MQ. Gọi P là giao điểm của hai phần đường tròn này.
Bước 3. Dùng thước vẽ các đoạn thẳng QP và NP.
Khi đó ta được hình bình hành MNPQ.
Bài 4. Cho hình thang cân PQRS có độ dài đáy PQ = 10 cm, đáy RS ngắn hơn đáy PQ là 6 cm, độ dài cạnh bên PS bằng một nửa độ dài đáy PQ. Tính chu vi của hình thang cân PQRS.
Lời giải:
Đáy RS ngắn hơn đáy PQ là 6 cm nên độ dài đáy RS là:
10 – 6 = 4 (cm)
Độ dài cạnh bên PS bằng một nửa độ dài đáy PQ nên độ dài cạnh bên PS là:
10 : 2 = 5 (cm)
Vì PQRS là hình thang cân nên hai cạnh bên PS và QR bằng nhau
Nên QR = PS = 5 cm.
Chu vi của hình thang cân PQRS là:
PQ + RS + QR + PS = 10 + 4 + 5 + 5 = 24 (cm)
Vậy chu vi của hình thang PQRS là 24 cm.
Bài 5. Cho các hình sau đây:
(1) Đoạn thẳng AB.
(2) Tam giác đều ABC.
(3) Hình tròn tâm O.
(4) Hình thang cân ABCD (có đáy lớn CD)
(5) Hình thoi ABCD.
Trong các hình nói trên:
a) Hình nào có trục đối xứng? Chỉ ra trục đối xứng của hình đó.
b) Hình nào có tâm đối xứng? Chỉ ra tâm đối xứng của hình đó.
Lời giải:
a) Cả 5 hình đã cho đều có trục đối xứng như sau:
(1) Đoạn thẳng AB là hình có 1 trục đối xứng và trục đối xứng là đường thẳng d đi qua trung điểm O của đoạn thẳng AB và vuông góc với AB.
(2) Tam giác đều ABC là hình có trục đối xứng và có 3 trục đối xứng d1, d2, d3 như sau:
(3) Hình tròn tâm O có vô số trục đối xứng và mỗi trục đối xứng là một đường thẳng đi qua tâm O của nó.
(4) Hình thang cân ABCD (có đáy lớn CD) là hình có 1 trục đối xứng và trục đối xứng là đường thẳng đi qua trung điểm H và K của 2 đáy AB và CD:
(5) Hình thoi ABCD có 2 trục đối xứng là hai đường chéo AC và BD
b) Trong 5 hình đã cho: đoạn thẳng AB, hình tròn tâm O, hình thoi ABCD là các hình có tâm đối xứng. Các hình tam giác đều ABC, hình thang cân ABCD là hình không có tâm đối xứng.
(1) Đoạn thẳng AB là hình có tâm đối xứng và tâm đối xứng là trung điểm O của AB
(3) Hình tròn tâm O có tâm đối xứng chính là tâm O
(5) Hình thoi ABCD có tâm đối xứng là giao điểm O của hai đường chéo AC và BD
Bài 6. Hãy quan sát xung quanh và chỉ ra những hình:
a) Có trục đối xứng.
b) Có tâm đối xứng
c) Vừa có trục đối xứng vừa có tâm đối xứng.
Lời giải:
a) Một số hình có trục đối xứng:
+) Hoa văn trang trí trên gạch hoa
+) Hình mặt cười
+) Hình con bướm
b) Một số hình có tâm đối xứng:
+) Hình biển báo giao thông
+) Hình chữ S
+) Hình chữ Z
c) Một số hình vừa có tâm đối xứng vừa có trục đối xứng
+) Hình trang trí bông hoa
+) Lục giác đều
+) Hình vuông
Bài 7. Hãy tìm và kể ra một số ứng dụng của tính đối xứng trong thực tiễn mà em biết.
Lời giải:
Một số ứng dụng của tính đối xứng trong thực tiễn:
+) Làm hình trang trí nghệ thuật
+) Thiết các các công trình kiến trúc
Nhà thờ Mosque (nhà thờ Hồi Giáo) tại Abu Dhabi.
Tháp Phước Duyên ở chùa Thiên Mụ (Huế)
Bài 8.
a) Một hình thoi có cạnh 4 cm thì chu vi của nó bằng bao nhiêu?
b) Một hình vuông có chu vi là 40 cm thì cạnh của nó bằng bao nhiêu?
c) Một hình chữ nhật có chu vi 30 cm và chiều rộng là 7 cm thì chiều dài của nó bằng bao nhiêu?
d) Một hình chữ nhật có chu vi 36 cm và chiều dài gấp đôi chiều rộng thì mỗi cạnh của nó bằng bao nhiêu?
Lời giải:
Để làm bài tập này, ta cần nhớ cách tính chu vi của các hình: hình thoi, hình vuông, hình chữ nhật (xem kiến thức ở các bài học).
a) Chu vi hình thoi có cạnh 4 cm là: 4 . 4 = 16 (cm)
b) Hình vuông có chu vi 40 cm thì có độ dài cạnh là: 40 : 4 = 10 (cm)
c) Một hình chữ nhật có chu vi 30 cm và chiều rộng là 7 cm.
Nửa chu vi của hình chữ nhật là: 30 : 2 = 15 (cm)
Chiều dài của hình chữ nhật là: 15 – 7 = 8 (cm)
d) Nửa chu vi hình chữ nhật là: 36 : 2 = 18 (cm)
Chiều dài gấp đôi chiều rộng, hay chiều rộng bằng chiều dài, khi đó ta có sơ đồ:
Tổng số phần bằng nhau là: 1 + 2 = 3 (phần)
Giá trị một phần hay chiều rộng là: 18 : 3 = 6 (cm)
Chiều dài là: 6 . 2 = 12 (cm)
Vậy chiều dài và chiều rộng của hình chữ nhật lần lượt là 12 cm và 6 cm.
Bài 9. Trên mảnh đất có dạng hình chữ nhật với chiều dài là 28 m và chiều rộng là 24 m, người ta định xây dựng một vườn hoa hình chữ nhật và bớt ra một phần đường đi như ở Hình 99.
a) Tính diện tích mảnh đất có dạng hình chữ nhật đó.
b) Tính diện tích vườn hoa.
c) Người ta định dùng những viên gạch chống trượt có dạng hình vuông có cạnh là 50 cm để lát đường đi. Cần dùng bao nhiêu viên gạch như thế? Biết rằng diện tích các mối nối và sự hao hụt là không đáng kể.
d) Người ta làm hàng rào xung quanh vườn hoa. Tính chiều dài hàng rào đó.
Lời giải:
a) Diện tích mảnh đất hình chữ nhật là:
28 . 24 = 672 (m2)
b) Quan sát hình 99, ta thấy sau khi bớt ra một phần đường đi thì phần vườn trồng hoa có dạng hình chữ nhật với:
Chiều dài phần vườn trồng hoa là: 28 – 1 – 1 = 26 (m)
Chiều rộng phần vườn trồng hoa là: 24 – 1 – 1 = 22 (m)
Diện tích phần vườn hoa là:
26 . 22 = 572 (m2)
c) Diện tích phần đường đi chính là hiệu diện tích mảnh đất với diện tích phần vườn hoa. Do đó diện tích phần đường đi là:
672 – 572 = 100 (m2)
Đổi 100 m2 = 1 000 000 cm2
Một viên gạch hình vuông có diện tích là:
50 . 50 = 2 500 (cm2)
Cần dùng số viên gạch là:
1 000 000 : 2 500 = 400 (viên gạch)
d) Phần chiều dài hàng rào xung quanh vườn hoa chính là chu vi phần vườn hoa có dạng hình chữ nhật
Vậy chiều dài hàng rào là: (22 + 26) . 2 = 96 m.
Bài 10. Bạn Thảo muốn cắt miếng bìa màu xanh có diện tích là 28 cm2 như Hình 100. Biết chu vi hình vuông ABCD là 16 cm. Tính giúp bạn Thảo độ dài cạnh EG.
Lời giải:
Miếng bìa màu xanh như Hình 100 được tạo bởi 1 hình vuông ABCD có chu vi là 16 cm và 4 phần bìa bằng nhau có dạng hình thang cân như hình ABGE.
Độ dài cạnh của hình vuông ABCD là: 16 : 4 = 4 (cm)
Hay AB = 4 cm
Diện tích hình vuông ABCD là: 4 . 4 = 16 (cm2)
Diện tích phần còn lại (cả mảnh bìa trừ đi phần hình vuông ABCD) là:
28 – 16 = 12 (cm)
Diện tích phần còn lại của miếng bìa là tổng diện tích của 4 hình thang cân.
Do đó diện tích hình thang cân ABGE là: 12 : 4 = 3 (cm2)
Hình thang cân ABGE có diện tích 3 cm2 và có đáy AB = 4 cm, chiều cao 1 cm
Khi đó ta có: hay
Suy ra: EG = 3 . 2 : 1 – 4 = 2 (cm)
Vậy độ dài cạnh EG là 2 cm.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Cánh diều hay, chi tiết khác:
Lý thuyết Chương 2: Số nguyên
Lý thuyết Chương 3: Hình học trực quan
Lý thuyết Chương 4: Một số yếu tố thống kê và xác suất
Lý thuyết Chương 5: Phân số và số thập phân
Lý thuyết Chương 6: Hình học phẳng
- Sách bài tập Toán 7 (Kết nối tri thức) Ôn tập chương 3
Giải SBT Toán lớp 7 Ôn tập chương 3
Giải trang 47 Tập 1
A. Câu hỏi (trắc nghiệm)
Câu hỏi 1 trang 47 Tập 1: Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?
A. và ;
B. và ;
C. và ;
D. và .
Lời giải:
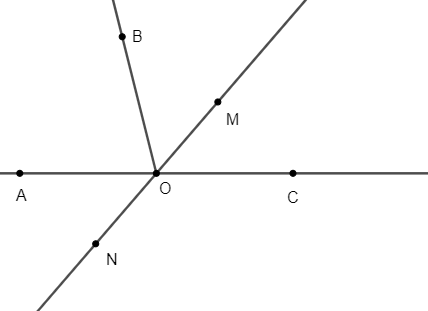
Từ hình vẽ ta thấy cặp góc đối đỉnh là và vì OA là tia đối của tia OC và OM là tia đối của tia ON.
Đáp án đúng là C.
Câu hỏi 2 trang 47 Tập 1: Trong các khẳng định sau, khẳng định nào đúng?
A. Hai góc bằng nhau thì đối đỉnh;
B. Hai góc không đối đỉnh thì không bằng nhau;
C. Hai góc đối đỉnh thì bằng nhau;
D. Cả ba khẳng định trên đều đúng.
Lời giải:
Khẳng định đúng là: Hai góc đối đỉnh thì bằng nhau.
Đáp án đúng là C.
Câu hỏi 3 trang 47 Tập 1: Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Biết số đo của một trong bốn góc đó là 65o. Khi đó số đo của ba góc còn lại là:
A. 65o; 115o; 120o;
B. 65o; 65o; 115o;
C. 115o; 115o; 50o;
D. 65o; 115o; 115o.
Lời giải:
Giả sử: đừng thẳng a cắt đường thẳng b tại O, tạo thành 4 góc và = 65o.
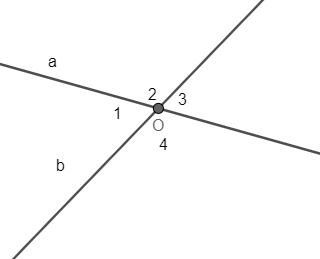
Vì và đối đỉnh nên = = 65o.
Vì và kề bù nên + = 180o.
Thay số: 65o + = 180o
= 180o – 65o = 115o.
Mà và đối đỉnh nên = = 115o.
Vậy = = 115o; = = 65o.
Đáp án đúng là D.
Câu hỏi 4 trang 47 Tập 1: Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào trong các trường hợp sau đây?
A. 70o; 70o; 70o; 110o;
B. 60o; 120o; 120o;120o;
C. 80o; 50o; 130o; 100o;
D. 90o; 90o; 90o; 90o.
Lời giải:
Vì hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt nên sẽ có hai cặp góc đối đỉnh.
Mà các góc đối đỉnh thì bằng nhau. Do đó, trong bốn giá trị sẽ lần lượt có hai cặp giá trị góc bằng nhau.
Nhận thấy chỉ có đáp án D thỏa mãn.
Vậy đáp án đúng là D.
Câu hỏi 5 trang 47 Tập 1: Hai đường thẳng AB và CD cắt nhau tại O. Cho OM là tia phân giác của góc BOD và . Số đo của góc AOC bằng:
A. 30o;
B. 60o;
C. 120o;
D. Một kết quả khác.
Lời giải:
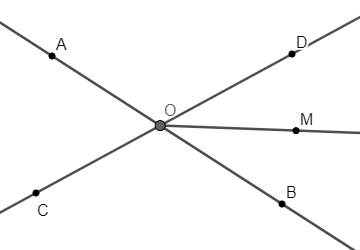
Vì OM là tia phân giác của góc BOD nên
Suy ra = 2.30o = 60o.
Lại có, và là hai góc đối đỉnh nên = = 60o.
Đáp án đúng là B.
Giải trang 48 Tập 1
Câu hỏi 6 trang 48 Tập 1: Cho Hình 3.29
a) Cặp góc so le trong là cặp góc:
A. ;
B. ;
C. ;
D. .
b) Cặp góc đồng vị là cặp góc:
A. ;
B. ;
C. ;
D. .
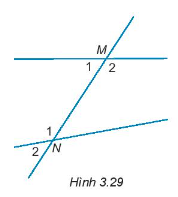
Lời giải:
a) Quan sát hình vẽ ta thấy cặp góc so le trong là: .
Đáp án đúng là D.
b) Quan sát hình vẽ ta thấy cặp góc đồng vị là:
Đáp án đúng là C.
Câu hỏi 7 trang 48 Tập 1: Cho Hình 3.30. Cặp góc A1; B1 là cặp góc:
A. So le trong;
B. Đối đỉnh;
C. Đồng vị;
D. Cả ba phương án trên đều sai.
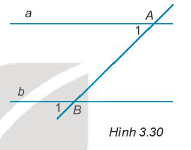
Lời giải:
Quan sát hình vẽ ta thấy cặp góc A1 và B1 ở vị trí đồng vị.
Đáp án đúng là C.
Câu hỏi 8 trang 48 Tập 1: Cho Hình 3.31, đường thẳng a song song với đường thẳng b nếu:
A. ;
B. ;
C. ;
D. .
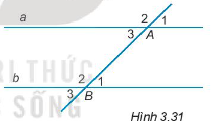
Lời giải:
Nếu có một đường thẳng cắt hai đường thẳng tạo thành các cặp góc so le trong bằng nhau hoặc các cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
Vậy để a song song với b thì các cặp góc so le trong bằng nhau hoặc các cặp góc đồng vị bằng nhau.
sai vì hai góc này không so le trong hay đồng vị;
sai vì hai góc này không so le trong hay đồng vị;
sai vì hai góc này không so le trong hay đồng vị;
đúng vì hai góc này ở vị trí so le trong.
Đáp án đúng là D.
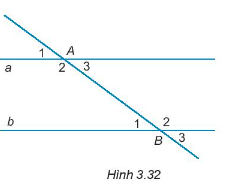
Câu hỏi 9 trang 48 Tập 1: Cho Hình 3.32, biết a // b. Khẳng địn nào sau đây là sai?
A. ;
B. ;
C. ;
D. .
Lời giải:
Vì a // b nên tạo ra những góc so le trong bằng nhau và những góc đồng vị bằng nhau.
sai vì hai góc này ở vị trí đồng vị nên chúng phải bằng nhau;
đúng vì hai góc này so le trong;
đúng vì hai góc này so le trong;
đúng vì hai góc này đồng vị.
Giải trang 49 Tập 1
B. Bài tập
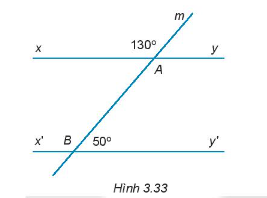
Bài 3.33 trang 49 Tập 1: Cho Hình 3.33. Hãy chứng minh xy // x’y’
Lời giải:
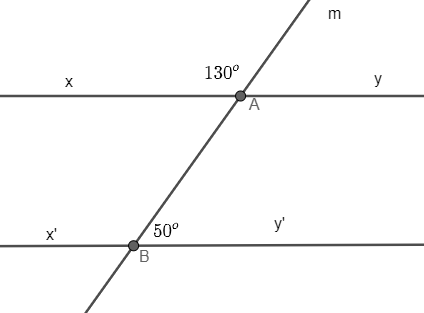
Ta có: và là hai góc kề bù.
Do đó, + = 180o
Thay số, 130o + = 180o.
= 180o – 130o = 50o.
Lại có, và là hai góc kề bù và = = 50o.
Do đo, xy // x’y’.
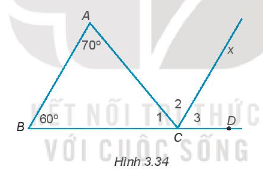
Bài 3.34 trang 49 Tập 1: Cho Hình 3.34. Biết AB // Cx, .
Tính số đo các góc .
Lời giải:
Vì AB song song với Cx nên các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
Ta có:
và là hai góc ở vị trí đồng vị nên = = 60o;
và là hai góc ở vị trí đồng vị nên = = 70o;
Ta có: + + = 180o.
Thay số: + 70o + 60o = 180o
= 180o – 60o – 70o.
= 50o
Vậy = 50o; = 70o; = 60o.
Bài 3.35 trang 49 Tập 1: Cho Hình 3.35. Biết CN là tia phân giác của góc ACM.
a) Chứng minh rằng CN // AB.
b) Tính số đo của góc A.
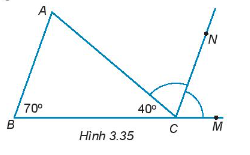
Lời giải:
a) Ta có: và là hai góc kề bù nên + = 180o.
Thay số, 40o + = 180o
= 180o – 40o
= 140o
Vì CN là tia pân giác của góc nên
Ta có: và ở vị trí đồng vị và = = 70o.
Do đó, AB song song CN.
b) Vì AB song song với CN nên các cặp góc so le trong sẽ bằng nhau và các cặp góc đồng vị sẽ bằng nhau.
Ta có: và là hai góc so le trong. Do đó, = = 70o.
Vậy = 70o.
Giải trang 50 Tập 1
Bài 3.36 trang 50 Tập 1: Cho Hình 3.36. Bên trong góc BOD vẽ tia Ox song song với AB. Biết .
a) Tính số đo của góc BOx.
b) Chứng minh Ox // CD và AB // CD.
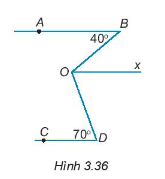
Lời giải:
a) Vì Ox song song với AB nên các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
Ta có: và là hai góc so le trong. Do đó, = = 40o.
Vậy = 40o.
b) Ta có:
Thay số, 110o = 40o +
= 110o – 40o
= 70o
Ta có: = 70o mà hai góc này ở vị trí so le trong nên Ox // CD.
Lại có Ox // AB nên AB //CD (điều phải chứng minh).
Bài 3.37 trang 50 Tập 1: Trong Hình 3.37 có BE // AC, CF //AB. Biết .
a) Chứng minh rằng .
b) Tính số đo của các góc BCF và ACB.
c) Gọi Bx, Cy lần lượt là tia phân giác của các góc BE và ACF. Chứng minh rằng Bxx // Cy.
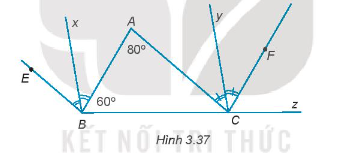
Lời giải:
a) Vì BE song song với AC nên các góc so le trong bằng nhau.
Do đó, (hai góc so le trong) (1)
Vì CF song song với AB nên các góc so le trong bằng nhau.
Do đó, (hai góc so le trong) (2)
Từ (1) và (2) suy ra = 80o.
b) Vì CF song song với AB nên các góc đồng vị bằng nhau.
Do đó, = (hai góc đồng vị)
Do đó, = = 60o.
Ta có, và là hai góc kề bù nên + = 180o.
Thay số , + 60o = 180o
= 180o – 60o
= 120o.
Ta có:
= +
120o = 80o +
= 120o – 80o
= 40o.
Vậy = 40o; = 120o.
c) Vì Bx là tia phân giác của góc nên
Vì Cy là tia phân giác của góc nên
Ta có BC cắt Bx và cắt Cy tạo ra cặp góc đồng vị là và .
Ta có:
= + = 40o + 60o = 100o.
= + = 40o + 60o = 100o.
Suy ra, = = 100o
Vì và là hai góc đồng vị và = nên Bx // Cy.
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 11: Định lí và chứng minh định lí
Ôn tập chương 3
Bài 12: Tổng các góc trong một tam giác
Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
- Sách bài tập Toán 6 (Kết nối tri thức) Ôn tập chương 3 trang 61, 62
Giải SBT Toán lớp 6 Ôn tập chương 3 trang 61, 62
Câu hỏi (Trắc Nghiệm)
Bài 1 trang 61 sách bài tập Toán lớp 6 Tập 1: Tìm khẳng định đúng trong các khẳng định sau:
So sánh ba số 0; 3 và -12.
(A) 0 < 3 < -12;
(B) 0 < -12 < 0;
(C) 3 < -12 < 0;
(D) -12 < 0 < 3.
Lời giải:
Vì -12 là số nguyên âm nên – 12 < 0 mà 0 < 3 nên -12 < 0 < 3
Đáp án cần chọn là: D
Bài 2 trang 61 sách bài tập Toán lớp 6 Tập 1: Tìm khẳng định đúng trong các khẳng định sau:
Cho tập hợp A = { x ∈ Z | -15 ≤ x < 7}
(A) -15 ∈ A và 7 ∈ A;
(B) -15 ∉ A và 7 ∈ A;
(C) -15 ∈ A và 7 ∉ A;
(D) -15 ∉ A và 7 ∉ A.
Lời giải:
Các phần tử thuộc A là số nguyên lớn hơn hoặc bằng -15 và nhỏ hơn 7.
Do đó: -15 ∈ A và 7 ∉ A
Đáp án cần chọn là: C
Bài 3 trang 61 sách bài tập Toán lớp 6 Tập 1: Tìm khẳng định đúng trong các khẳng định sau:
Hai số nguyên a và b có tích a. b dương và tổng a + b dương. Khi đó:
(A) a > 0 và b > 0;
(B) a > 0 và b < 0;
(C) a < 0 và b > 0;
(D) a < 0 và b < 0.
Lời giải:
Vì hai số nguyên a và b có tích a. b dương nên a và b là hai số nguyên cùng dấu
Mà tổng a + b dương nên a > 0 và b > 0
Bài 4 trang 61 sách bài tập Toán lớp 6 Tập 1: Tìm khẳng định đúng trong các khẳng định sau:
Hai số nguyên a và b có tích a. b dương và tổng a + b âm. Khi đó:
(A) a > 0 và b > 0;
(B) a > 0 và b < 0;
(C) a < 0 và b > 0;
(D) a < 0 và b < 0.
Lời giải:
Vì hai số nguyên a và b có tích a. b dương nên a và b là hai số nguyên cùng dấu
Mà tổng a + b âm nên a < 0 và b < 0
Đáp án cần chọn là: D
Bài 5 trang 61 sách bài tập Toán lớp 6 Tập 1: Tìm khẳng định đúng trong các khẳng định sau:
Hai số nguyên a và b có tích a. b âm và hiệu a – b âm. Khi đó:
(A) a > 0 và b > 0;
(B) a > 0 và b < 0;
(C) a < 0 và b > 0;
(D) a < 0 và b < 0.
Lời giải:
Vì hai số nguyên a và b có tích a. b âm nên a và b là hai số nguyên trái dấu
Mà hiệu a – b âm nên a < b.
Do vậy a < 0; b > 0
Đáp án cần chọn là: C
Bài 6 trang 61 sách bài tập Toán lớp 6 Tập 1: Tìm khẳng định đúng trong các khẳng định sau:
Hai số nguyên a và b có tích a. b âm và hiệu a – b dương. Khi đó:
(A) a > 0 và b > 0;
(B) a > 0 và b < 0;
(C) a < 0 và b > 0;
(D) a < 0 và b < 0.
Lời giải:
Vì hai số nguyên a và b có tích a. b âm nên a và b là hai số nguyên trái dấu
Mà hiệu a – b dương nên a > b.
Do vậy a > 0; b < 0
Đáp án cần chọn là: B
Bài tập
Bài 3.41 trang 62 sách bài tập Toán lớp 6 Tập 1: Số nguyên a có phần dấu là – và phần số tự nhiên là 27. Hãy viết số a và tìm số đối của a.
Lời giải:
+) Vì số nguyên a có phần dấu là “-” và phần số tự nhiên là 27 nên a = – 27
+) Số đối của – 27 là 27.
Vậy a = -27, số đối của a là 27.
Bài 3.42 trang 62 sách bài tập Toán lớp 6 Tập 1: Hãy sắp xếp các số a, b, c, d theo thứ tự tăng dần, nếu:
a = 32 + (-28); b = (-7) – 5; c = (-12). (-5); d = (-28): 7.
Lời giải:
Ta có:
a = 32 + (-28) = 32 – 28 = 4
b = (-7) – 5 = – 7 – 5 = – (7 + 5) = – 12
c = (-12). (-5) = 12. 5 = 60
d = (-28): 7 = – (28: 7) = -4
Vì 12 > 4 nên -12 < -4 mà – 4 < 4 < 60 nên -12 < -4 < 4 < 60 hay b < d < a < c.
Vậy sắp xếp theo thứ tự tăng dần là: b; d; a; c.
Bài 3.43 trang 62 sách bài tập Toán lớp 6 Tập 1: Tính giá trị của biểu thức; tìm cách tính hợp lí:
a) 21. 23 – 3. 7. (-17);
b) 42. 3 – 7. [(-34) + 18].
Lời giải:
a) 21. 23 – 3. 7. (-17) = 21. 23 – 21. (-17) = 21. [23 – (-17)] = 21. (23 + 17) = 21. 40
= 21. 4. 10 = (21. 4). 10 = 84. 10 = 840.
b) 42. 3 – 7. [(-34) + 18] = 7. 6. 3 – 7. [(-34) + 18] = 7. 18 – 7. [(-34) + 18]
= 7. [18 – (- 34) – 18] = 7. [(18 – 18) + 34] = 7. (0 + 34) = 7. 34 = 238.
Bài 3.44 trang 62 sách bài tập Toán lớp 6 Tập 1: Tính giá trị của biểu thức; tìm cách tính hợp lí:
a) 71. 64 + 32. (-7) – 13. 32;
b) 13. (23 – 17) – 13. (23 + 17).
Lời giải:
a) 71. 64 + 32. (-7) – 13. 32
= 71. 2. 32 + 32. (-7) – 13. 32
= 32. [71. 2 + (-7) – 13]
= 32. (142 – 7 – 13)
= 32. (135 – 13)
= 32. 122
= 3 904.
b) 13. (23 – 17) – 13. (23 + 17)
= 13. 23 – 13. 17 – 13. 23 – 13. 17
= (13. 23 – 13. 23) – (13. 17 + 13. 17)
= 0 – 2. (13. 17)
= 0 – 2. 221
= 0 – 442
= -442.
Bài 3.45 trang 62 sách bài tập Toán lớp 6 Tập 1: Tìm x, nếu (38 – x). (x + 25) = 0.
Lời giải:
Tích hai thừa số bằng 0 chỉ xảy ra khi một trong hai thừa số bằng 0
(38 – x). (x + 25) = 0
Suy ra 38 – x = 0 hoặc x + 25 = 0
Trường hợp 1:
38 – x = 0
x = 38 – 0
x = 38
Trường hợp 2:
x + 25 = 0
x = 0 – 25
x = -25
Vậy x = 38, x = -25.
Bài 3.46 trang 62 sách bài tập Toán lớp 6 Tập 1: Tìm các bội của 6 lớn hơn -19 và nhỏ hơn 19.
Lời giải:
Nhân 6 lần lượt với 0; 1; 2; 3; 4; … ta được các bội dương của 6 là: 0; 6; 12; 18; 24; …
Do đó các bội của 6 là: …; – 24; -18; -12; -6; 0; 6; 12; 18; 24; …
Mà bội của 6 lớn hơn -19 và nhỏ hơn 19 là: -18; -12; -6; 0; 6; 12; 18
Vậy các bội của 6 lớn hơn -19 và nhỏ hơn 19 là -18; -12; -6; 0; 6; 12; 18.
Bài 3.47 trang 62 sách bài tập Toán lớp 6 Tập 1: Tìm tất cả các ước chung của hai số 36 và 42.
Lời giải:
+) Ta đi tìm các ước chung nguyên dương của 36 và 42.
Ta có: 36 = 22.32; 42 = 2. 3. 7
ƯCLN(36, 42) = 2. 3 = 6
ƯC(36, 42) = Ư(6) = {1; 2; 3; 6}
Do đó tất cả các ước chung của hai số 36 và 42 là: -6; -3; -2; -1; 1; 2; 3; 6
Vậy tất cả các ước chung của hai số 36 và 42 là: -6; -3; -2; -1; 1; 2; 3; 6 viết gọn là ±1; ±2; ±3; ±6.
Bài 3.48 trang 62 sách bài tập Toán lớp 6 Tập 1: Hãy điền các số nguyên thích hợp thay thế các dấu “?” trong bảng dưới đây sao cho tích của ba số ở ba ô liền nhau luôn bằng 120.
?
?
6
?
?
?
?
?
?
-4
?
Lời giải:
Giả sử bốn số ở bốn ô liên tiếp nào đó là a, b, c và d. Khi đó theo điều kiện của bài toán ta có: abc = bcd = 120. Từ đây ta suy ra a = d. Điều này có nghĩa là các số nằm ở ô thứ nhất, thứ tư, thứ bảy, thứ mười bằng nhau; các ô nằm ở ô thứ ba, thứ sáu, thứ chín bằng nhau; các ô nằm ở ô thứ hai, thứ năm, thứ tám, thứ mười một bằng nhau.
Chú ý rằng ô thứ mười là số -4 nên các số nằm ở ô thứ nhất, thứ tư, thứ bảy đều là số -4
Ô thứ ba là số 6 nên các số nằm ở ô thứ ba, thứ sáu, thứ chín đều là số 6.
Đặt các ô còn lại chứa số x, ta có bảng sau:

Ta có: (-4). x. 6 = 120
x. (-24) = 120
x = 120: (-24)
x = -5
Vậy ta được kết quả bảng là:

Bài 3.49 trang 62 sách bài tập Toán lớp 6 Tập 1: Hãy điền các số nguyên thích hợp thay thế các dấu “?” trong bảng dưới đây sao cho tổng của ba số ở ba ô liền nhau luôn bằng 0.
?
-7
?
?
?
?
?
?
3
?
?
Lời giải:
Giả sử bốn số ở bốn ô liên tiếp nào đó là a, b, c và d. Khi đó theo điều kiện của bài toán ta có: a + b + c = b + c + d = 0. Từ đây ta suy ra a = d. Điều này có nghĩa là các số nằm ở ô thứ hai, thứ năm, thứ tám, thứ mười một bằng nhau; các ô nằm ở ô thứ ba, thứ sáu, thứ chín bằng nhau; các ô nằm ở ô thứ nhất, thứ tư, thứ bảy, thứ mười bằng nhau.
Chú ý rằng ô thứ hai là số -7 nên các số nằm ở ô thứ năm, thứ tám, thứ mười một đều là số -7
Ô thứ chín là số 3 nên các số nằm ở ô nằm ở ô thứ ba, thứ sáu đều là số 3.
Đặt các ô còn lại chứa số x, ta có bảng sau:

Ta có: x + (-7) + 3 = 0
x – 7 + 3 = 0
x – 7 = 0 – 3
x – 7 = -3
x = -3 + 7
x = 4
Vậy ta được kết quả bảng là:
