Câu hỏi:
Cho tam giác ABC và d là đường thẳng tùy ý qua B. Qua E là điểm bất kì trên AC, vẽ đường thẳng song song với AB và BC, lần lượt cắt d tại M và N. Gọi D là giao điểm của ME và BC. Đường thẳng NE cắt AB và MC lần lượt tại F và K. Chứng minh:a) b)
Trả lời:
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có đường phân giác trong AD. Qua C kẻ đường thẳng song song với AB, cắt tia AD tại E. Chứng minh:a) ΔABD∽ΔECD; b) ΔACE cân tại C
Câu hỏi:
Cho tam giác ABC có đường phân giác trong AD. Qua C kẻ đường thẳng song song với AB, cắt tia AD tại E. Chứng minh:a) b) cân tại C
Trả lời:
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hình thang ABCD (AB||CD), có DAB^=CBD^.Chứng minh ΔABD∽ΔBDC.
Câu hỏi:
Hình thang ABCD (AB||CD), có .Chứng minh
Trả lời:
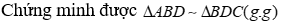
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có AM là phân giác của BAC^M∈BC. Kẻ tia Cx thuộc nửa mặt phẳng bờ BC không chứa A sao cho BCx^=12BAC^. Gọi N là giao của Cx và tia AM. Chứng minh:a) ∆BAM ~ ∆NCMb) ∆ABM ~ ∆ANCc) Tam giác BCN cân.
Câu hỏi:
Cho tam giác ABC có AM là phân giác của . Kẻ tia Cx thuộc nửa mặt phẳng bờ BC không chứa A sao cho Gọi N là giao của Cx và tia AM. Chứng minh:a) b) c) Tam giác BCN cân.
Trả lời:
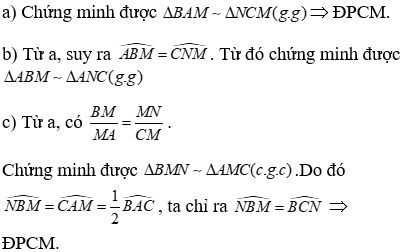
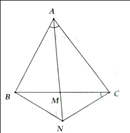
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có đường phân giác trong AD. Qua C kẻ đường thẳng song song với AB, cắt tia AD tại E. Chứng minh:a) ΔABD∽ΔECD; b) ΔACE cân tại C
Câu hỏi:
Cho tam giác ABC có đường phân giác trong AD. Qua C kẻ đường thẳng song song với AB, cắt tia AD tại E. Chứng minh:a) b) cân tại C
Trả lời:
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC vuông tại A, đường cao AH. Chứng minha) AB2=BH.BC;b) AH2=BH.HC.
Câu hỏi:
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minha) b)
Trả lời:
a) Chứng minh được
b) HS tự chứng minh
====== **** mời các bạn xem câu tiếp bên dưới **** =====