Cho tam giác ABC cân tại A và điểm M tùy ý nằm trong tam giác. Kẻ tia Mx song song vói BC cắt AB ở D, tia My song song với AC cắt BC ỏ E. Chứng minh  DME^=900+A^2.

Câu hỏi:

Cho tam giác ABC cân tại A và điểm M tùy ý nằm trong tam giác. Kẻ tia Mx song song vói BC cắt AB ở D, tia My song song với AC cắt BC ỏ E. Chứng minh  $\widehat{DME}={90}^0+\frac{\widehat{A}}{2}.$

Trả lời:

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình thang cân ABCD (AB // CD) có A^=2C^. Tính các góc của hình thang cân
   
   

   Câu hỏi:
   

   Cho hình thang cân ABCD (AB // CD) có $\widehat{A}=2\widehat{C}$. Tính các góc của hình thang cân

   Trả lời:

   Ta có $\widehat{A}+\widehat{D}={180}^0, \widehat{A}=2\widehat{C}=2\widehat{D}$Suy ra $\widehat{C}=\widehat{D}={60}^0,\widehat{A}=\widehat{B}={120}^0$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình thang cân ABCD (AB // CD) có A^=3D^. Tính các góc của hình thang cân.
   
   

   Câu hỏi:
   

   Cho hình thang cân ABCD (AB // CD) có $\widehat{A}=3\widehat{D}$. Tính các góc của hình thang cân.

   Trả lời:

   Tương tự bài 1A. Ta có: $\widehat{C}=\widehat{D}={45}^0,\widehat{A}=\widehat{B}={135}^0$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hình thang cân ABCD (AB // CD) có AH và BK là hai đường cao của hình thang.a) Chứng minh DH = CD−AB2. b) Biết AB = 6 cm, CD = 14 cm, AD = 5 cm, tính DH, AH và diện tích hình thang cân ABCD.
   
   

   Câu hỏi:
   

   Cho hình thang cân ABCD (AB // CD) có AH và BK là hai đường cao của hình thang.a) Chứng minh DH = $\frac{CD-AB}{2}.$ b) Biết AB = 6 cm, CD = 14 cm, AD = 5 cm, tính DH, AH và diện tích hình thang cân ABCD.

   Trả lời:

   a) Chứng minhDADH = DBCK (ch-gnh)Þ DH = CKVận dụng nhận xét hình thang ABKH (AB//KH) có AH//BK Þ AB = HKb) Vậy $DH=\frac{CD-AB}{2}$ c) DH = 4cm, AH = 3cm; S_ABCD = 30cm²

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
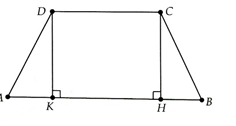
4. Cho hình thang cân ABCD (AB//CD) có A^=B^=600, AB = 4,5cm; AD = BC = 2 cm. Tính độ dài đáy CD và diện tích hình thang cân ABCD
   
   

   Câu hỏi:
   

   Cho hình thang cân ABCD (AB//CD) có $\widehat{A}=\widehat{B}={60}^0$, AB = 4,5cm; AD = BC = 2 cm. Tính độ dài đáy CD và diện tích hình thang cân ABCD

   Trả lời:

   Hạ CH và DK vuông góc với ABTa có:$AK=BH=\frac{1}{2}AD=1cm$ Từ đó: CD = 2,5cm$CH=\sqrt{3}cm$$S_{ABCD}=\frac{\left(AB+CD\right).CD}{2}=\frac{7\sqrt{3}}{2}c{m}^2$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến của tam giác. Chứng minh BCDE là hình thang cân
   
   

   Câu hỏi:
   

   Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến của tam giác. Chứng minh BCDE là hình thang cân

   Trả lời:

   Sử dụng tính chất đường trung bình, ta chứng minh được DE//BC

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====