Cho hình chữ nhật ABCD, E là điểm tùy ý trên AB.Chứng minh rằng: SABCD=2SECD

Câu hỏi:

Cho hình chữ nhật ABCD, E là điểm tùy ý trên AB.Chứng minh rằng: $S_{ABCD}=2S_{ECD}$

Trả lời:

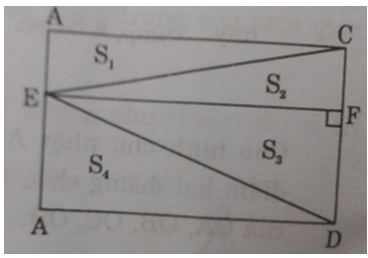Kẻ EF ⊥ CD ⇒ AC // EF // ADXét ΔBCE và ΔFEC có:(CAE) = (CFE) = 90o(BCE) = (CEF) (Hai góc so le trong)CE chung⇒ ΔBCE = ΔFEC (cạnh huyền- góc nhọn)tương tự ΔAED=ΔFDE.Do đó (theo hình vẽ):S1 = S2 và S3 = S4⇒ S2 + S3 = S1 + S4 = (1/2)SABCDHay SECD = (1/2)SABCD ⇒ SABCD = 2SECD.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình vuông ABCD, M là trung điểm của CD, N là trung điểm của AD. Gọi I là giao điểm của AM và BN.Chứng minh rằng: ∆BAN=∆ADM
   
   

   Câu hỏi:
   

   Cho hình vuông ABCD, M là trung điểm của CD, N là trung điểm của AD. Gọi I là giao điểm của AM và BN.Chứng minh rằng: $∆BAN=∆ADM$

   Trả lời:

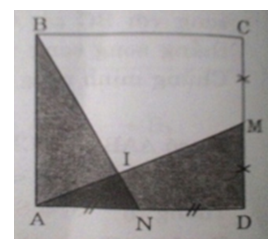
   Xét ΔBAN và ΔADM có:AB = AD (ABCD là hình vuông)(BAN) = (ADM) = 90oAN = MD (= 1/2 cạnh hình vuông)⇒ ΔBAN = ΔADM (c.g.c)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====