Câu hỏi:
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) Hai tứ giác AEFD, AECF là những hình bình hành;
Trả lời:
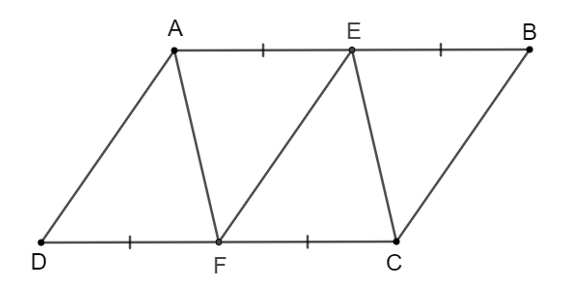
a) Vì ABCD là hình bình hành nên AB = CD, AB // CD.
Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE, CF = DF.
Do đó AE = BE = CF = DF.
• Xét tứ giác AEFD có:
AE // DF (vì AB // CD);
AE = DF (chứng minh trên)
Do đó tứ giác AEFD là hình bình hành.
• Xét tứ giác AECF có:
AE // CF (vì AB // CD);
AE = CF (chứng minh trên)
Do đó tứ giác AECF là hình bình hành.
Vậy hai tứ giác AEFD, AECF là những hình bình hành.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hai con đường lớn a và b cắt nhau tạo thành một góc. Bên trong góc đó có một điểm dân cư O. Phải mở một con đường thẳng đi qua O như thế nào để theo con đường đó, hai đoạn đường từ điểm O đến con đường a và b bằng nhau (các con đường đều là đường thẳng) (H.3.27)?
Câu hỏi:
Hai con đường lớn a và b cắt nhau tạo thành một góc. Bên trong góc đó có một điểm dân cư O. Phải mở một con đường thẳng đi qua O như thế nào để theo con đường đó, hai đoạn đường từ điểm O đến con đường a và b bằng nhau (các con đường đều là đường thẳng) (H.3.27)?

Trả lời:
Sau bài học này ta giải quyết được bài toán như sau:
Gọi điểm giao nhau giữa hai đường thẳng a và b là điểm O
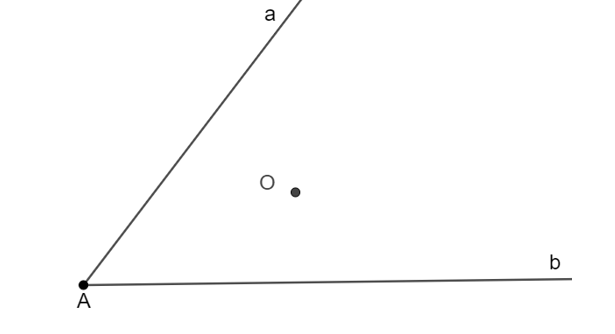
– Vẽ tia Ax đi qua điểm O. Trên tia Ax lấy điểm B sao cho OA = OB.
– Qua B vẽ tia By // Ab; Bz // Aa cắt hai tia Aa và Bb lần lượt tại hai điểm C và D
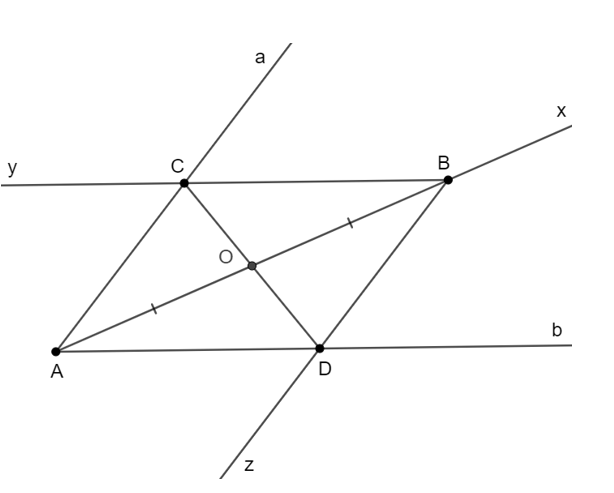
Khi đó, tứ giác ACBD là hình bình hành (vì AC // BD; AD // BC) có O là trung điểm AB nên O là trung điểm của CD.
Hai đoạn đường từ điểm O đến con đường a và b bằng nhau, tức là OC = OD.
Vậy con đường cần mở đường thẳng đi qua hai điểm C và D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong Hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?
Câu hỏi:
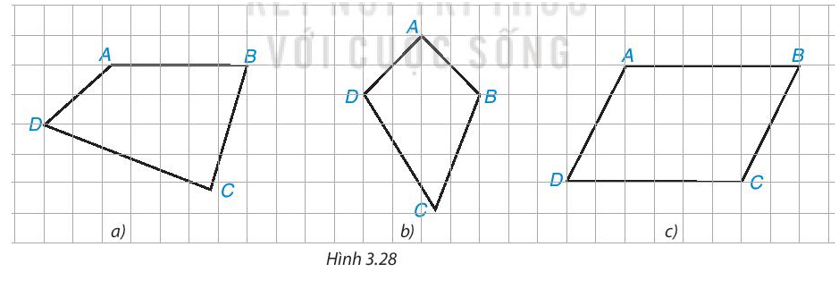
Trong Hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?
Trả lời:
Tứ giác trong Hình 3.28c là hình bình hành vì:
Ta so sánh độ dài các cạnh đối trong tứ giác bằng cách đếm số ô vuông trong hình.
Ta thấy AB = CD; AD = BC.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Vẽ hình bình hành, biết hai cạnh liên tiếp bằng 3 cm, 4 cm và góc xen giữa hai cạnh đó bằng 60o. Hãy mô tả cách vẽ và giải thích tại sao hình vẽ được là hình bình hành.
Câu hỏi:
Vẽ hình bình hành, biết hai cạnh liên tiếp bằng 3 cm, 4 cm và góc xen giữa hai cạnh đó bằng 60o. Hãy mô tả cách vẽ và giải thích tại sao hình vẽ được là hình bình hành.
Trả lời:
Giả sử hình bình hành ABCD có AD = 3cm, AB = 4 cm và .
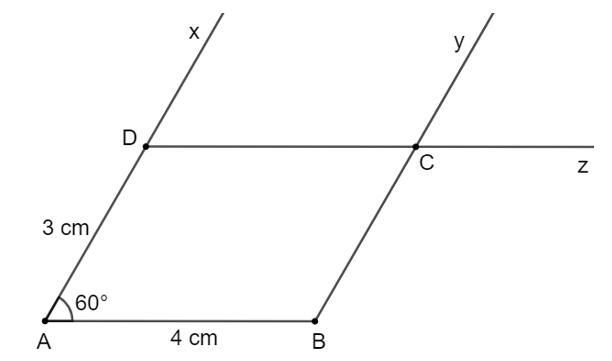
Cách vẽ:
– Vẽ cạnh AB = 4 cm.
– Vẽ . Trên tia Ax lấy điểm D sao cho AD = 3cm.
– Kẻ By // AD, Dz // BC. Hai tia By và Dz cắt nhau tại C, ta được hình bình hành ABCD.
Hình vẽ được là hình bình hành vì có hai cặp cạnh đối song song (AB // CD, AD // BC).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hãy nêu các tính chất của hình bình hành mà em đã biết.
Câu hỏi:
Hãy nêu các tính chất của hình bình hành mà em đã biết.
Trả lời:
Các tính chất của hình bình hành mà em đã biết:
– Hai cặp cạnh đối song song.
– Hai cặp cạnh đối bằng nhau.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình bình hành ABCD (H.3.30).
a) Chứng minh ∆ABC = ∆CDA.
Từ đó suy ra AB = CD, AD = BC và ABC^=CDA^.
Câu hỏi:
Cho hình bình hành ABCD (H.3.30).
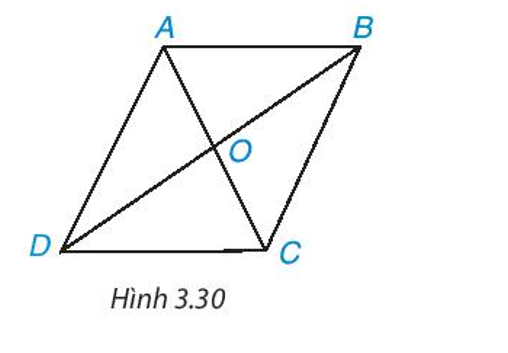
a) Chứng minh ∆ABC = ∆CDA.
Từ đó suy ra AB = CD, AD = BC và .Trả lời:
a) Vì ABCD là hình bình hành nên AB // CD; AD // BC.
Suy ra (hai góc so le trong).
Xét ∆ABC và ∆CDA có:
(chứng minh trên);
Cạnh AC chung.
(chứng minh trên);
Do đó ∆ABC = ∆CDA (g.c.g).
Suy ra AB = CD, AD = BC (các cặp cạnh tương ứng); (hai góc tương ứng).====== **** mời các bạn xem câu tiếp bên dưới **** =====