Câu hỏi:
Cho hình bình hành ABCD có Trên cạnh BC lấy M sao cho BM = 4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng DC tại N.a) Tính tỉ số IB/IDb) Chứng minh ΔMAB và ΔAND đồng dạngc) Tính độ dài DN và CNd) Chứng minh
Trả lời:
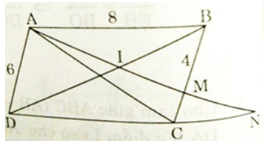 a) AD // BC (gt)
a) AD // BC (gt)![]() b) Xét ΔAMB và ΔNAD có:∠BAM = ∠ AND (so le trong, AB // CD)∠ABM = ∠ADN (góc đối của hình bình hành)⇒ ΔAMB ∼ ΔNAD (g.g)c) ΔAMB ∼ ΔNAD (cmt)
b) Xét ΔAMB và ΔNAD có:∠BAM = ∠ AND (so le trong, AB // CD)∠ABM = ∠ADN (góc đối của hình bình hành)⇒ ΔAMB ∼ ΔNAD (g.g)c) ΔAMB ∼ ΔNAD (cmt)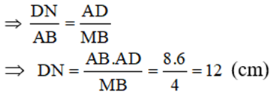 Do đó: CN = DN – DC = 12 – 8 = 4 (cm)d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có![]() Tương tự, do AD // BM nên
Tương tự, do AD // BM nên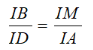
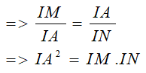
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Phần trắc nghiệm (3 điểm)Cho tam giác MNP có MI là tia phân giác (I ∈ NP) . Ta có:
Câu hỏi:
Phần trắc nghiệm (3 điểm)Cho tam giác MNP có MI là tia phân giác (I ∈ NP) . Ta có:
A.
B.
C.
D.
Đáp án chính xác
Trả lời:
Chọn D
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đoạn thẳng AB có chiểu dài gấp 4 lần đoạn thẳng CD, độ dài đoạn thẳng CD gấp 10 lần độ dài đoạn thẳng EF. Tỉ số của hai đoạn thẳng AB và EF là:
Câu hỏi:
Cho đoạn thẳng AB có chiểu dài gấp 4 lần đoạn thẳng CD, độ dài đoạn thẳng CD gấp 10 lần độ dài đoạn thẳng EF. Tỉ số của hai đoạn thẳng AB và EF là:
A.
B. 40
Đáp án chính xác
C.
D.
Trả lời:
Chọn B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ΔABC có độ dài các cạnh AB = 6cm; AC = 7cm và AD là đường phân giác. Khi đó:
Câu hỏi:
Cho ΔABC có độ dài các cạnh và AD là đường phân giác. Khi đó:
A.
Đáp án chính xác
B.
C.
D.
Trả lời:
Chọn B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Chọn câu khẳng định sai. Nếu tam giác ABC đồng dạng với tam giác DEF thì:
Câu hỏi:
Chọn câu khẳng định sai. Nếu tam giác ABC đồng dạng với tam giác DEF thì:
A.
B.
C.
D.
Đáp án chính xác
Trả lời:
Chọn D
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có độ dài các cạnh AB = 4cm, AC = 5cm và BC = 6cm và tam giác MNP có độ dài các cạnh MN = 3cm, MP = 2cm, NP = 2,5cm thì:
Câu hỏi:
Cho tam giác ABC có độ dài các cạnh và tam giác MNP có độ dài các cạnh thì:
A.
Đáp án chính xác
B.
C.
Trả lời:
Chọn A
====== **** mời các bạn xem câu tiếp bên dưới **** =====