Cho ABCD là một hình bình hành. Giải thích tại sao tứ giác ABCD có bốn cạnh bằng nhau trong mỗi trường hợp sau: Trường hợp 1: AB = AD. Trường hợp 2: AC vuông góc với BD. Trường hợp 3: AC là phân giác góc BAD. Trường hợp 4: BD là phân giác góc ABC.

Câu hỏi:

Cho ABCD là một hình bình hành. Giải thích tại sao tứ giác ABCD có bốn cạnh bằng nhau trong mỗi trường hợp sau:
Trường hợp 1: AB = AD.
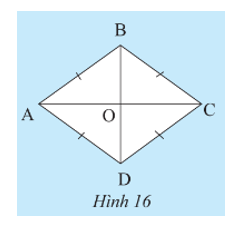
Trường hợp 2: AC vuông góc với BD.
Trường hợp 3: AC là phân giác góc BAD.
Trường hợp 4: BD là phân giác góc ABC.

Trả lời:

• Trường hợp 1: AB = AD.

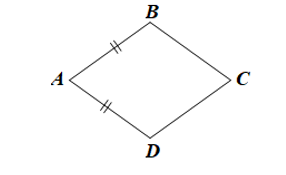
Vì ABCD là hình bình hành nên AD = BC và AB = CD.
Lại có AB = AD (giả thiết)
Do đó AB = AD = BC = CD.
• Trường hợp 2: AC vuông góc với BD.

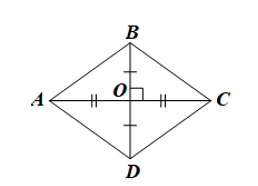
Vì ABCD là hình bình hành nên AD = BC, AB = CD và hai đường chéo AC, BD cắt nhau tại trung điểm O của mỗi đường.
Xét DOAB và DOCB có:
$\widehat{AOB}=\widehat{COB}=90°$; OB là cạnh chung; OA = OC
Do đó DOAB = DOCB (hai cạnh góc vuông)
Suy ra AB = CB (hai cạnh tương ứng).
Mà AD = BC và AB = CD nên AB = CD = CB = DA.
• Trường hợp 3: AC là phân giác góc BAD.

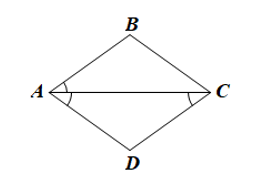
Vì ABCD là hình bình hành nên AB // CD
Do đó $\widehat{BAC}=\widehat{CDA}$ (so le trong).
Mà $\widehat{BAC}=\widehat{CAD}$  (do AC là tia phân giác của góc BAD)
Suy ra $\widehat{CAD}=\widehat{CDA}$ .
Tam giác ACD có $\widehat{CAD}=\widehat{CDA}$ nên là tam giác cân tại D
Suy ra DA = DC.
Lại có AB = CD và AD = BC (chứng minh trên).
Do đó AB = BC = CD = DA.
• Trường hợp 4: BD là phân giác góc ABC.
Chứng minh tương tự như trường hợp 3 ta cũng có AB = BC = CD = DA.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Quan sát hình chụp các mái nhà ở phố cổ Hội An, em thấy các cạnh đối của tứ giác ABCD có gì đặc biệt?       
   
   

   Câu hỏi:
   

   Quan sát hình chụp các mái nhà ở phố cổ Hội An, em thấy các cạnh đối của tứ giác ABCD có gì đặc biệt?       
   

   Trả lời:

   Quan sát hình chụp các mái nhà ở phố cổ Hội An, ta thấy các cạnh đối của tứ giác ABCD vừa song song vừa bằng nhau (AB // DC, AB = DC và AD // BC, AD = BC).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Hình 1a là hình ảnh của một thước vẽ truyền dùng để phóng to hay thu nhỏ một hình vẽ có sẵn. Dùng thước đo góc để đo số đo của các cặp góc A^1 và D^, C^1 và D^ của tứ giác ABCD (Hình 1b) rồi rút ra nhận xét về mối quan hệ giữa các cặp cạnh AB và CD; AD và BC.
   
   

   Câu hỏi:
   

   Hình 1a là hình ảnh của một thước vẽ truyền dùng để phóng to hay thu nhỏ một hình vẽ có sẵn. Dùng thước đo góc để đo số đo của các cặp góc ${\widehat{A}}_1$ và $\widehat{D}$, ${\widehat{C}}_1$ và $\widehat{D}$ của tứ giác ABCD (Hình 1b) rồi rút ra nhận xét về mối quan hệ giữa các cặp cạnh AB và CD; AD và BC.
   

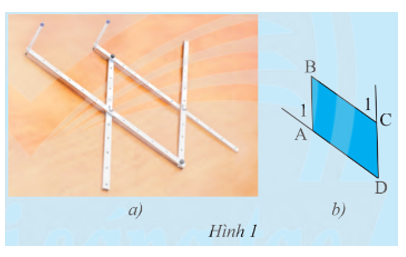
   Trả lời:

   Dùng thước đo góc ta xác định được ${\widehat{A}}_1=\widehat{D}$ và ${\widehat{C}}_1=\widehat{D}$.
   Ta có ${\widehat{A}}_1=\widehat{D}$ và hai góc này ở vị trí đồng vị nên AB // CD.
   ${\widehat{C}}_1=\widehat{D}$ và hai góc này ở vị trí đồng vị nên AD // BC.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tứ giác ABCD có các cạnh đối song song. Gọi O là giao điểm của hai đường chéo. Hãy chứng tỏ: ‒ Tam giác ABC bằng tam giác CDA. ‒ Tam giác OAB bằng tam giác OCD.
   
   

   Câu hỏi:
   

   Cho tứ giác ABCD có các cạnh đối song song. Gọi O là giao điểm của hai đường chéo. Hãy chứng tỏ:
   ‒ Tam giác ABC bằng tam giác CDA.
   ‒ Tam giác OAB bằng tam giác OCD.
   

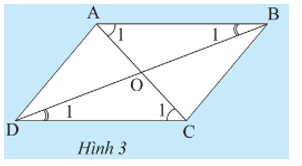
   Trả lời:

   
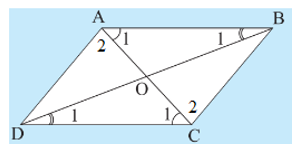
   • Tứ giác ABCD có AB // DC và AD // BC.
   Từ AB // DC suy ra ${\widehat{A}}_1={\widehat{C}}_1$ (so le trong) và ${\widehat{B}}_1={\widehat{D}}_1$ (so le trong).
   Từ AD // BC suy ra ${\widehat{A}}_2={\widehat{C}}_2$ (so le trong).
   Xét DABC và DCDA có:
   ${\widehat{A}}_1={\widehat{C}}_1$; AC là cạnh chung; ${\widehat{A}}_2={\widehat{C}}_2$
   Do đó DABC = DCDA (g.c.g).
   • Do DABC = DCDA nên AB = CD (hai cạnh tương ứng).
   Xét DOAB và DOCD có:
   ${\widehat{A}}_1={\widehat{C}}_1$; AB = CD; ${\widehat{B}}_1={\widehat{D}}_1$ (chứng minh trên)
   Do đó DOAB = DOCD (g.c.g).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình bình hành PQRS với I là giao điểm của hai đường chéo (Hình 4). Hãy chỉ ra các đoạn thẳng bằng nhau và các góc bằng nhau có trong hình.
   
   

   Câu hỏi:
   

   Cho hình bình hành PQRS với I là giao điểm của hai đường chéo (Hình 4). Hãy chỉ ra các đoạn thẳng bằng nhau và các góc bằng nhau có trong hình.
   

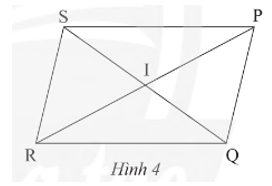
   Trả lời:

   Trong hình bình hành PQRS với I là giao điểm của hai đường chéo, ta có:
   • Các đoạn thẳng bằng nhau: PQ = RS; PS = QR; IP = IR; IS = IQ.
   • Các góc bằng nhau: $\widehat{PQR}=\widehat{PSR};$ $\widehat{SPQ}=\widehat{SRQ};$ $\widehat{RSQ}=\widehat{SQP};$ $\widehat{PSQ}=\widehat{SQR};$  $\widehat{PRQ}=\widehat{RPS};$ $\widehat{SIR}=\widehat{PIQ};$ $\widehat{SIP}=\widehat{QIR};$ $\widehat{SIQ}=\widehat{PIR}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Cho biết độ dài hai cạnh của tứ giác này là 4 cm và 5 cm. Tìm độ dài hai cạnh còn lại.
   
   

   Câu hỏi:
   

   Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Cho biết độ dài hai cạnh của tứ giác này là 4 cm và 5 cm. Tìm độ dài hai cạnh còn lại.
   

   Trả lời:

   Giả sử mắt lưới của lưới bóng chuyền có dạng hình tứ giác ABCD có các cạnh đối song song và độ dài hai cạnh là 4 cm, 5 cm.
   Tứ giác ABCD có các cạnh đối song song nên là hình bình hành. Giả sử AB = 4 cm, AD = 5 cm.
   Do đó CD = AB = 4 cm; BC = AD = 5 cm.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====