b) Tứ giác MNPB là hình gì? Tại sao?

Câu hỏi:

b) Tứ giác MNPB là hình gì? Tại sao?

Trả lời:

b) Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra NP // AB hay NP // MB.
Tứ giác MNPB có MN // BP; BM // NP (chứng minh trên).
Do đó, tứ giác MNPB là hình bình hành.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

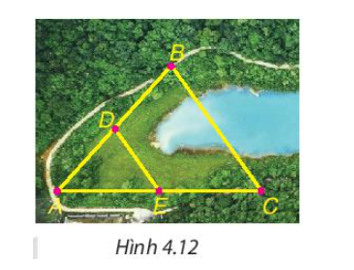
1. Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
   
   

   Câu hỏi:
   

   Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
   

   Trả lời:

   Sau bài học này ta giải quyết được bài toán như sau:
   Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.
   Suy ra DE là đường trung bình của tam giác ABC.
   Do đó $DE=\frac{1}{2}BC$ suy ra BC = 2DE = 2 . 500 = 1 000 (m)
   Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
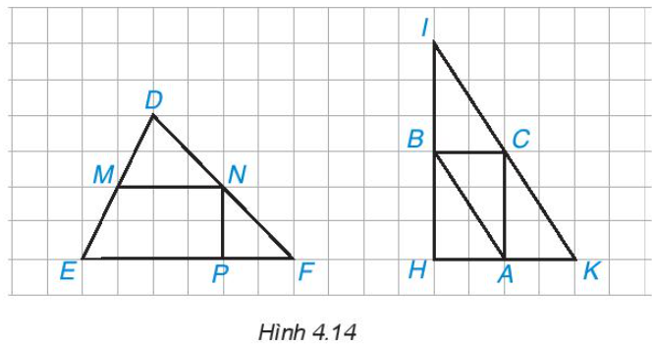
2. Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.
   
   

   Câu hỏi:
   

   Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.
   

   Trả lời:

   Quan sát Hình 4.14, ta thấy:
   * Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.
   * Xét ∆IHK có:
   • B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆DEF.
   • B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆DEF.
   • A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆DEF.
   Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho DE là đường trung bình của tam giác ABC (H.4.15 Sử dụng định lí Thalès đảo, chứng minh rằng DE // BC.
   
   

   Câu hỏi:
   

   Cho DE là đường trung bình của tam giác ABC (H.4.15
   
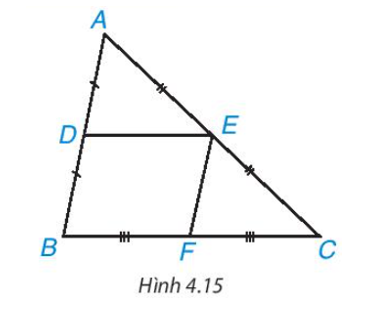
   Sử dụng định lí Thalès đảo, chứng minh rằng DE // BC.

   Trả lời:

   Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
   AE = EC và E ∈ AC nên E là trung điểm của AC.
   Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho DE là đường trung bình của tam giác ABC (H.4.15 Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra DE=12BC.
   
   

   Câu hỏi:
   

   Cho DE là đường trung bình của tam giác ABC (H.4.15
   

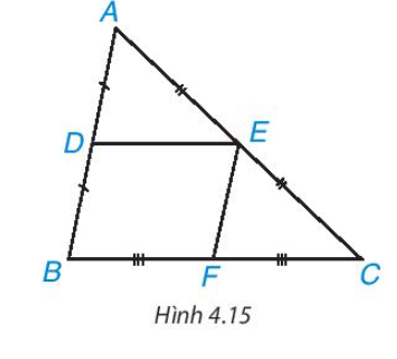
   Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra $DE=\frac{1}{2}BC$.

   Trả lời:

   Vì DE là đường trung bình của tam giác ABC nên D, E lần lượt là trung điểm của AB, AC.
   Suy ra $AD=\frac{1}{2}AB;AE=\frac{1}{2}AC$.
   Do đó DE // BC (theo định lí Thalès đảo).
   Vì E, F lần lượt là trung điểm của AC, BC.
   Suy ra $EC=\frac{1}{2}AC;CF=\frac{1}{2}BC$.
   Do đó EF // AB (theo định lí Thalès đảo).
   Xét tứ giác DEFB có DE // BF (vì DE // BC); EF // BD (vì EF // AB)
   Do đó tứ giác DEFB là hình bình hành.
   Suy ra DE = BF mà $BF=\frac{1}{2}BC$ nên $DE=\frac{1}{2}BC$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?
   
   

   Câu hỏi:
   

   Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?

   Trả lời:

   
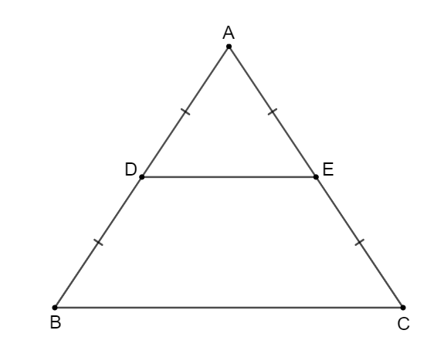
   Tam giác ABC cân tại A nên $\widehat{B}=\widehat{C}$.
   Vì D và E lần lượt là trung điểm của AB, AC nên DE là đường trung bình của tam giác ABC.
   Suy ra DE // BC nên tứ giác DECB là hình thang.
   Hình thang DECB có $\widehat{B}=\widehat{C}$ nên tứ giác DECB là hình thang cân.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====