Lý thuyết Định lí Pythagore (Cánh diều 2023) hay, chi tiết | Lý thuyết Toán lớp 8

Lý thuyết Toán lớp 8 Bài 1: Định lí Pythagore

A. Lý thuyết Định lí Pythagore

1. Định lí Pythagore

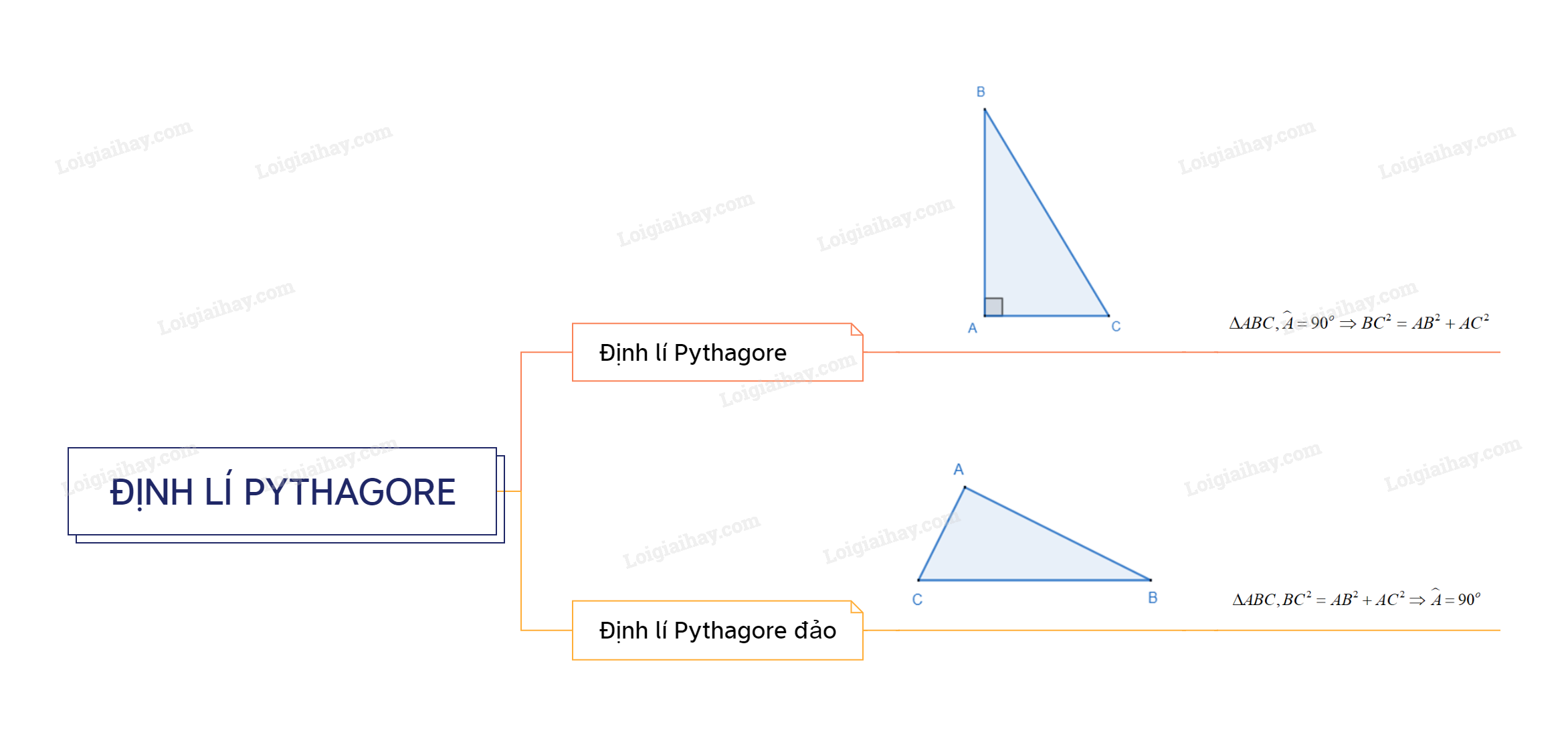
Trong một tam giác vuông, bình phương độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.

$\mathrm{\Delta }ABC,\hat{A}={90}^o\Rightarrow B{C}^2=A{B}^2+A{C}^2$

  

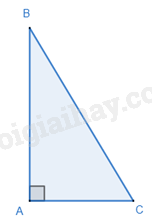
2. Định lí Pythagore đảo

Nếu một tam giác có bình phương độ dài của một cạnh bằng tổng các bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.

 

$\mathrm{\Delta }ABC,B{C}^2=A{B}^2+A{C}^2\Rightarrow \hat{A}={90}^o$

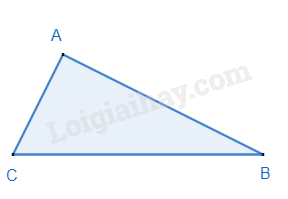
Ví dụ:

Tam giác ABC có AB = 3cm, BC = 5cm, AC = 4cm thì tam giác ABC vuông tại A do $3^2+4^2=5^2$, suy ra$$B{C}^2=A{B}^2+A{C}^2$$

 

B. Bài tập Định lí Pythagore

Bài 1. Cho tam giác ABC vuông tại A, tính độ dài cạnh còn lại trong các trường hợp sau:

a) AB = 5 cm, AC = 12 cm;

b) $AB= \sqrt{3}cm,BC=12cm$ ;

c) AB – AC = 7 cm, AB + AC = 17 cm.

Hướng dẫn giải

a) Do tam giác ABC vuông tại A nên áp dụng định lý Pythagore, ta có:

BC² = AB² + AC²

Suy ra BC² = 5² + 12² = 25 + 144 = 169.

Do đó $BC =\sqrt{169}=13\text{ (}cm)$

Vậy BC = 13 cm.

b) Áp dụng định lý Pythagore vào tam giác ABC vuông tại A, ta có:

BC² = AB² + AC²

Suy ra $A{C}^2=B{C}^2–A{B}^2={12}^2–{\left(\sqrt{3}\right)}^2=144–3=141$

Do đó $AC=\sqrt{141}=11,87\left(cm\right)$

Vậy AC = 11,87 cm.

c) Theo bài ta có: AB – AC = 7 suy ra AB = AC + 7

Mặt khác, AB + AC = 17 suy ra AC + 7 + AC = 17

Hay 2AC = 17 – 7 = 10 suy ra AC = 5 cm và AB = 12 cm

Do tam giác ABC vuông tại A nên áp dụng định lý Pythagore, ta có:

BC² = AB² + AC²

Suy ra BC² = 5² + 12² = 25 + 144 = 169.

Do đó $BC =\sqrt{169}=13\text{ (}cm)$ .

Vậy BC = 13 cm.

Bài 2. Cho tam giác ABC vuông tại A. Biết $\frac{AB}{AC}=\frac{4}{3}$  và BC = 20 cm. Tính độ dài các cạnh AB và AC.

Hướng dẫn giải

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A, ta có:

AB² + AC²  = BC² = 20² = 400.

Từ đề bài: $\frac{AB}{AC}=\frac{4}{3}$  hay $\frac{AB}{4}=\frac{AC}{3}$  suy ra $\frac{A{B}^2}{16}=\frac{A{C}^2}{9}$ .

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

 

$\frac{A{B}^2}{16}=\frac{A{C}^2}{9}=\frac{A{B}^2+A{C}^2}{16+9}=\frac{400}{25}=16$

AB²  = 16.16 suy ra AB = 16 cm.

AC² = 9 . 16 = 144 suy ra AC = 12 cm.

Vậy AB = 16 cm; AC = 12 cm.

Bài 3. Cho hình vẽ sau. Tìm giá trị của a.

Hướng dẫn giải

Áp dụng định lý Pythagore và tam giác ADE vuông tại A, ta có:

AD² + AE²  = DE²

AE²  = DE² – AD²

 Suy ra AE = 4.

Suy ra AB = AE + EB = 4 + 4 = 8.

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A, ta có:

AB² + AC²  = BC²

Suy ra BC² = 8² + 6² = 100 suy ra BC = 10 hay a = 10.

Vậy a = 10.

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 8 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 2: Hình chóp tứ giác đều

Lý thuyết Bài 1: Định lí Pythagore

Lý thuyết Bài 2: Tứ giác

Lý thuyết Bài 3: Hình thang cân

Lý thuyết Bài 4: Hình bình hành

Lý thuyết Bài 5: Hình chữ nhật