Tài liệu Hình bình hành gồm các nội dung chính sau:
I. Phương pháp giải
– tóm tắt lý thuyết ngắn gọn;
– phương pháp giải chi tiết từng dạng bài tập.
II. Một số ví dụ/ Ví dụ minh họa
– gồm 3 ví dụ minh họa đa dạng của các dạng bài tập trên có lời giải chi tiết.
III. Bài tập vận dụng
– gồm 15 bài tập vận dụng (15 bài tập có đáp án, có lời giải chi tiết) giúp học sinh tự rèn luyện cách giải các dạng bài tập Hình bình hành.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây: 
Hình bình hành
I. Phương pháp giải
1. Định nghĩa
Hình bình hành là tứ giác có các cạnh đối song song (h.4.1).
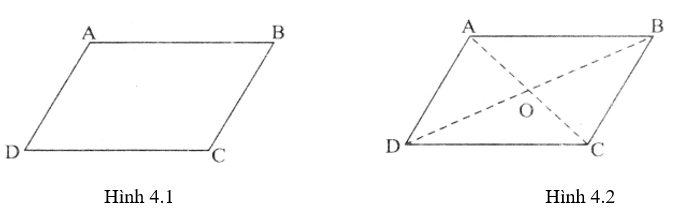
2. Tính chất
Trong hình bình hành (h.4.2):
· Các cạnh đối bằng nhau;
· Các góc đối bằng nhau;
· Hai đường chéo cắt nhau tại trung điểm mỗi đường.
3. Dấu hiệu nhận biết
– Tứ giác có các cạnh đối song song là hình bình hành;
– Tứ giác có các cạnh đối bằng nhau là hình bình hành;
– Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành;
– Tứ giác có các góc đối bằng nhau là hình bình hành;
– Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
II. Một số ví dụ
Ví dụ 1: Cho hình bình hành ACBD. Trên tia đối của tia AD lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho . Chứng minh rằng ba đường thẳng MN, AC, BD gặp nhau tại một điểm.
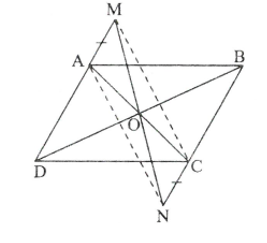
Giải (h.4.3)
* Tìm cách giải
AC và BD là hai đường chéo của hình bình hành ABCD nên chúng cắt nhau tại trung điểm O của AC. Ta còn phải chứng minh MN đi qua O. Muốn vậy chỉ cần chứng minh AMCN là hình bình hành để suy ra đường chéo MN đi qua trung điểm O của AC.
* Trình bày lời giải
Tứ giác: AMCN có và nên là hình bình hành. Suy ra hai đường chéo MN và AC cắt nhau tại trung điểm O của AC.
Mặt khác, ABCD là hình bình hành nên hai đường chéo BD và AC cắt nhau tại trung điểm O của AC.
Vậy các đường thẳng MN, BD và AC cùng đi qua trung điểm O của AC.
Nhận xét: Hai hình bình hành AMCD và ABCD có chung đường chéo AC thì các đường chéo của chúng đồng quy tại trung điểm của đường chéo chung
Xem thêm