Giải Toán 8 Bài 2: Hình thang

Giải bài tập Toán lớp 8 Bài 2: Hình thang

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 69 sgk Toán 8 Tập 1:

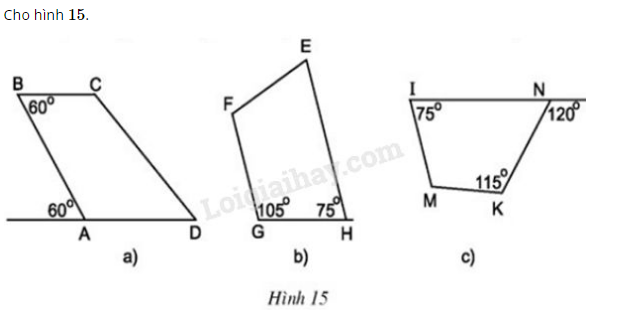
a) Tìm các tứ giác là hình thang.

Phương pháp giải: Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.

Lời giải:

Tứ giác $ABCD$ là hình thang vì $BC//AD$ (có hai góc so le trong bằng nhau) 

Tứ giác $EFGH$ là hình thang vì $FG//EH$ (có tổng hai góc trong cùng phía bằng ${105}^o+{75}^o={180}^o$)

Tứ giác $IMKN$ không phải là hình thang vì không có cặp cạnh đối nào song song (do IM không song song NK; góc N và góc K ở vị trí nhưng không bằng nhau nên MK không song song IN).

b) Có nhận xét gì về hai góc kề một cạnh bên của hình thang ?

Phương pháp giải: Quan sát và rút ra nhận xét

Lời giải:

Hai góc kề một cạnh bên của hình thang bù nhau.

Trả lời câu hỏi 2 trang 70 sgk Toán 8 Tập 1:

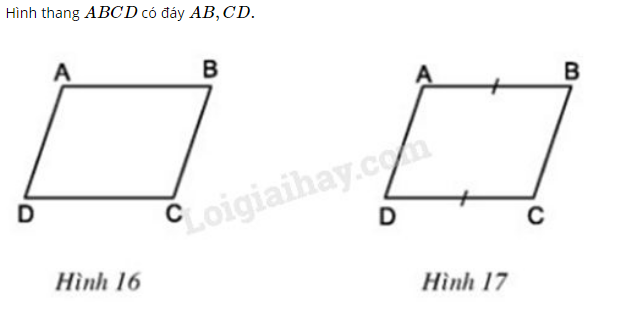
a) Cho biết $AD//BC$ (h.16). Chứng minh rằng $AD=BC,AB=CD.$

b) Cho biết $AB=CD$ (h.17). Chứng minh rằng $AD//BC,AD=BC.$

Phương pháp giải: Áp dụng:

– Xét hai tam giác bằng nhau

– Hai đường thẳng song song thì có cặp góc so le trong bằng nhau.

Lời giải:

a)

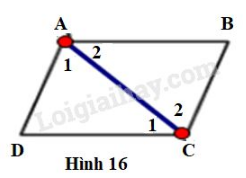
Hình thang $ABCD$ có đáy $AB,CD\Rightarrow AB//CD\Rightarrow \widehat{A_2}=\widehat{C_1}$ (hai góc so le trong) 

Lại có: $AD//BC$ $\Rightarrow \widehat{A_1}=\widehat{C_2}$ (hai góc so le trong)

Xét $\Delta ABC$ và $\Delta CDA$ có:

+) $\widehat{A_2}=\widehat{C_1}$ (chứng minh trên)

+) $AC$ chung

+) $\widehat{A_1}=\widehat{C_2}$ (chứng minh trên)

$\Rightarrow \Delta ABC=\Delta CDA$ (g.c.g)

$\Rightarrow AD=BC,AB=CD$ (các cặp cạnh tương ứng)

b)

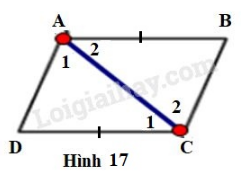
Hình thang $ABCD$ có đáy $AB,CD\Rightarrow AB//CD\Rightarrow \widehat{A_2}=\widehat{C_1}$ (hai góc so le trong) 

Xét $\Delta ABC$ và $\Delta CDA$ có:

+) $AC$ chung

+) $\widehat{A_2}=\widehat{C_1}$  (chứng minh trên)

+) $AB=CD$ (giả thiết)

$\Rightarrow \Delta ABC=\Delta CDA$ (c.g.c)

$\Rightarrow AD=BC$ (hai cạnh tương ứng)

$\Rightarrow$ $\widehat{A_1}=\widehat{C_2}$ (hai góc tương ứng)

Mặt khác $\widehat{A_1};\widehat{C_2}$ ở vị trí so le trong.

$\Rightarrow AD//BC$

Câu hỏi và bài tập (trang 70, 71 sgk Toán 8 Tập 1)

Bài 6 trang 70 sgk Toán 8 Tập 1: Dùng thước và êke, ta có thể kiểm tra được hai đường thẳng có song song với nhau hay không (xem hình ). Trên hình , có những tứ giác nào là hình thang, có những tứ giác nào không là hình thang. Bằng cách nêu trên, hãy kiểm tra xem trong các tứ giác ở hình , tứ giác nào là hình thang?

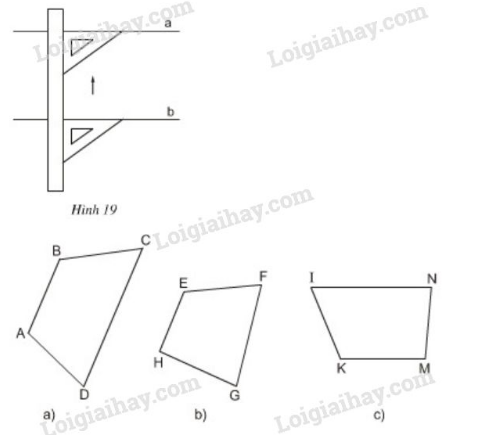
Phương pháp giải: Áp dụng:

– Định nghĩa hai đường thẳng song song: là hai đường thẳng không có điểm chung.

– Định nghĩa hình thang: Hình thang là tứ giác có hai cạnh đối song song.

Lời giải:

Các bước tiến hành:

– Xét xem cần phải kiểm tra hai cạnh nào thuộc hai đường thẳng song song với nhau.

– Đặt mép cạnh góc vuông của êke trùng với một trong hai cạnh cần kiểm tra.

– Đặt mép thước trùng với mép cạnh góc vuông còn lại của êke.

– Giữ nguyên vị trí thước, dời êke để xét xem cạnh góc vuông của êke có trùng với cạnh còn lại mà ta cần kiểm tra của tứ giác. Nếu chúng trùng nhau thì tứ giác đó là hình thang.

Bằng cách kiểm tra trên ta có kết quả như sau:

+) Tứ giác $ABCD$ có cạnh $AB$ song song với cạnh $DC$ nên tứ giác $ABCD$ là hình thang.

+) Tứ giác $IKMN$ có cạnh $IN$ song song với cạnh $KM$ nên tứ giác $IKMN$ là hình thang.

+) Tứ giác $EFGH$ không là hình thang vì không có cặp cạnh nào song song với nhau.

Bài 7 trang 71 sgk Toán 8 Tập 1:

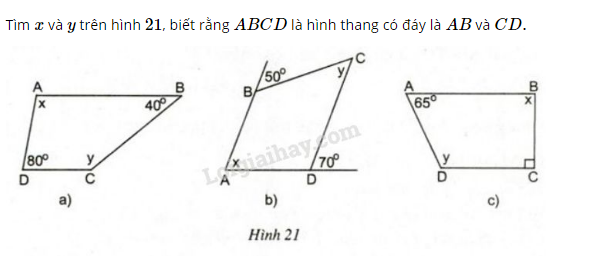
Phương pháp giải: Áp dụng các tính chất của một đường thẳng cắt hai đường thẳng song song: hai góc trong cùng phía bù nhau, hai góc đồng vị bằng nhau, hai góc so le trong bằng nhau.

Lời giải:

Vì $ABCD$ là hình thang có đáy là $AB$ và $CD$ nên $AB//CD$

$a)$ Ta có: $AB//DC$ (chứng minh trên) 

$\Rightarrow \hat{A}+\hat{D}={180}^0$ (hai góc trong cùng phía bù nhau)

$\Rightarrow x+{80}^0={180}^0$ 

$\Rightarrow x={180}^0-{80}^0={100}^0$

Ta có: $AB//DC$ (chứng minh trên)

$\Rightarrow \hat{C}+\hat{B}={180}^0$ (hai góc trong cùng phía bù nhau)

$\Rightarrow y+{40}^0={180}^0$

$\Rightarrow y={180}^0-{40}^0={140}^0$

$b)$ Vì $AB//DC$ (chứng minh trên)

$\Rightarrow x={70}^0$ (hai góc đồng vị bằng nhau)

$\Rightarrow y={50}^0$ (hai góc so le trong bằng nhau)

$c)$ Ta có $AB//DC$ (chứng minh trên)

$\Rightarrow \hat{B}+\hat{C}={180}^0$ (hai góc trong cùng phía bù nhau)

$\Rightarrow x+{90}^0={180}^0$

$\Rightarrow x={180}^0-{90}^0={90}^0$

Ta có $AB//DC$ (chứng minh trên)

$\Rightarrow \hat{D}+\hat{A}={180}^0$ (hai góc trong cùng phía bù nhau)

$\Rightarrow y+{65}^0={180}^0$

$\Rightarrow y={180}^0-{65}^0={115}^0$

Bài 8 trang 71 sgk Toán 8 Tập 1: Hình thang $ABCD$ ($AB//CD$) có $\hat{A}-\hat{D}={20}^0$   , $\hat{B}=2\hat{C}$. Tính các góc của hình thang.

Phương pháp giải: Áp dụng tính chất: Nếu một đường thẳng cắt hai đường thẳng song song thì tổng hai góc trong cùng phía bù nhau.
Lời giải:

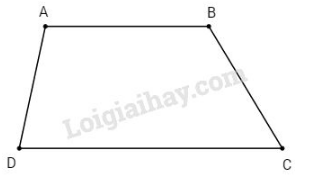
Vì $AB//CD$ nên $\hat{A}+\hat{D}={180}^0$  (1) (hai góc trong cùng phía bù nhau)

Ta có $\hat{A}-\hat{D}={20}^0$ (giả thiết) 

$\begin{array}{l}\Rightarrow \hat{A}=\hat{D}+{20}^0(2)\\ \text{Thay (2) vào (1) ta được:}\\ \Rightarrow \hat{A}+\hat{D}=\hat{D}+{20}^0+\hat{D}\\ =2\hat{D}+{20}^0={180}^0\\ \Rightarrow \hat{D}=\left({180}^0-{20}^0\right):2={80}^0.\end{array}$

Thay $\hat{D}={80}^0$ vào $\hat{A}={20}^0$ +$\hat{D}$ ta được $\hat{A}={20}^0+{80}^0={100}^0$

Lại có $\hat{B}=2\hat{C}$     (3) ;

Do $AB//CD$ nên $\hat{B}+\hat{C}={180}^0$   (4) (hai góc trong cùng phía bù nhau)

Thay (3) vào (4) ta được:

$2\hat{C}+\hat{C}={180}^0$

hay $3\hat{C}={180}^0\Rightarrow \hat{C}={180}^0:3={60}^0$

Do đó $\hat{B}=2\hat{C}={2.60}^0={120}^0$

Bài 9 trang 71 sgk Toán 8 Tập 1: Tứ giác $ABCD$ có $AB=BC$ và $AC$ tia phân giác của góc $A$. Chứng minh rằng $ABCD$ là hình thang.

Phương pháp giải: Áp dụng:

– Dấu hiệu nhận biết hình thang: Hình thang là tứ giác có hai cạnh đối song song.

– Chứng minh hai đường thẳng song song ta chứng minh cặp góc so le trong bằng nhau.

Lời giải:

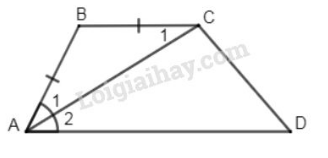
Ta có $AB=BC$ (giả thiết)

Suy ra  $∆ABC$ cân tại $B$ (định nghĩa tam giác cân)

Nên $\widehat{A_1}=\widehat{C_1}$ (1) (tính chất tam giác cân) 

Lại có, $AC$ là tia phân giác của $\hat{A}$ (giả thiết) nên suy ra $\widehat{A_1}=\widehat{A_2}$ (2) (tính chất tia phân giác )

Từ (1) và (2) suy ra $\widehat{C_1}=\widehat{A_2}$ mà hai góc này ở vị trí so le trong nên $BC//AD$

Vậy tứ giác $ABCD$ là hình thang.

Bài 10 trang 71 sgk Toán 8 Tập 1:

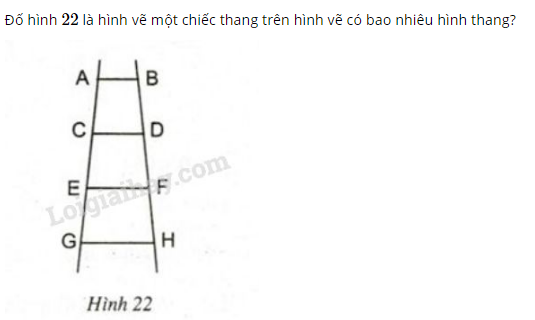
Phương pháp giải: Áp dụng dấu hiệu nhận biết hình thang: Hình thang là tứ giác có hai cạnh đối song song.

Lời giải:

Từ hình 22 ta có: $AB//CD//EF//GH$

Nên ta có tất cả $6$ hình thang, đó là: $ABDC,CDFE,EFHG,$ $ABFE,CDHG,ABHG.$

Lý thuyết hình thang

1. Các kiến thức cần nhớ:

* Hình thang: 

Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.

Hai góc kề một cạnh bên của hình thang có tổng bằng ${180}^0$

Nhận xét: 

+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.

+ Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.

+ Hình thang vuông là hình thang có một góc vuông.

Ví dụ 1:

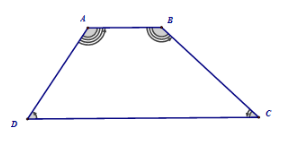
$ABCD$ là hình thang. Khi đó:

+ $AB//CD$ , $AB,CD$ là hai đáy, $AD,BC$ là cạnh bên.

+ $\hat{A}+\hat{D}=\hat{B}+\hat{C}={180}^{\circ }$

+ Nếu $AD//BC\iff \{\begin{array}{l}AD=BC\\ AB=CD\end{array}$

+ Nếu $AB=CD\iff \{\begin{array}{l}AD=BC\\ AD//BC\end{array}$

* Hình thang vuông:  là hình thang có  thì  là hình thang vuông.

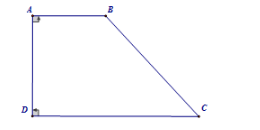
* Hình thang cân: 

Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.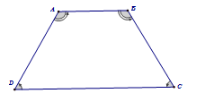

Tính chất:

+ Trong hình thang cân, hai cạnh bên bằng nhau.

+ Trong hình thang cân, hai đường chéo bằng nhau.

Dấu hiệu nhận biết:

+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

+ Hình thang có hai đường chéo bằng nhau là hình thang cân.

Ví dụ:

+ $ABCD$ là hình thang cân thì $AD=BC;AC=BD$

+ Tứ giác $ABCD$ có $\{\begin{array}{l}AB//CD\\ \hat{D}=\hat{C}\end{array}$ $\iff ABCD$ là hình thang cân.

+ Tứ giác $ABCD$ có $\{\begin{array}{l}AB//CD\\ \hat{A}=\hat{B}\end{array}$ $\iff ABCD$ là hình thang cân.

+ Tứ giác $ABCD$ có $\{\begin{array}{l}AB//CD\\ AC=BD\end{array}$ $\iff ABCD$ là hình thang cân.

2. Các dạng toán thường gặp:

Dạng 1: Chứng minh và tính các góc của hình thang, hình thang vuông hình thang cân dựa vào tính chất hình.

Phương pháp: Ta sử dụng các kiến thức:

+ Tính chất của hình thang, hình thang vuông, hình thang cân (ở trên)

+ Tổng bốn góc của một tứ giác bằng${360}^{\circ }$ .

+ Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.

+ Hai góc kề một cạnh bên của hình thang bằng ${180}^0$ .

Dạng 2: Chứng minh một tứ giác là hình thang, hình thang vuông, hình thang cân

Phương pháp: Ta sử dụng định nghĩa và các dấu hiệu nhận biết để chứng minh