Giải SGK Toán 8 Bài 4: Đường trung bình của tam giác, của hình thang

Giải bài tập Toán lớp 8 Bài 4: Đường trung bình của tam giác, của hình thang

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 76 Toán 8 Tập 1: Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB. Qua D vẽ đường thẳng song song với BC, đường thẳng này cắt AC ở E. Bằng quan sát, hãy nêu dự đoán về vị trí của điểm E trên cạnh AC.

Lời giải

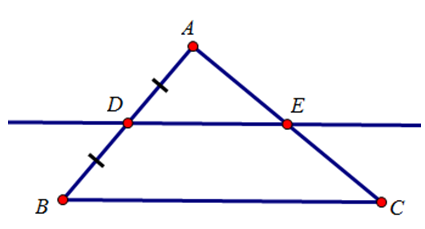
Dự đoán: E là trung điểm cạnh AC

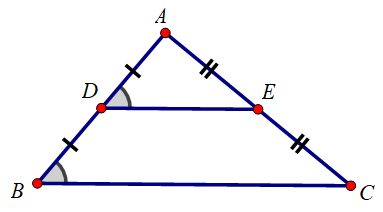
Câu hỏi 2 trang 77 Toán 8 Tập 1: Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB, trung điểm E của AC. Dùng thước đo góc và thước chia khoảng để kiểm tra rằng $\widehat{ADE}=\widehat{B}, DE=\frac{1}{2}BC$.

Lời giải

Câu hỏi 3 trang 77 Toán 8 Tập 1: Tính độ dài đoạn BC trên hình 33.

Giữa hai điểm B và C có chướng ngại vật (h.33). Biết DE = 50m, ta có thể tích được khoảng cách giữa hai điểm B và C.

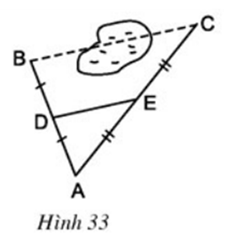
Lời giải

Xét $\Delta ABC,$ có:

D là trung điểm AB

E là trung điểm AC

Suy ra DE là đường trung bình của

$\Rightarrow DE=\frac{1}{2}BC$ hay BC = 2DE.

Mà DE = 50m nên BC = 2.50 = 100m.

Vậy khoảng cách giữa hai điểm B và C là 100m.

Câu hỏi 4 trang 78 Toán 8 Tập 1: Cho hình thang ABCD (AB // CD). Qua trung điểm E của AD kẻ đường thẳng song song với hai đáy, đường thẳng này cắt AC ở I, cắt BC ở F (h.37). Có nhận xét gì về vị trí của điểm I trên AC, điểm F trên BC ?

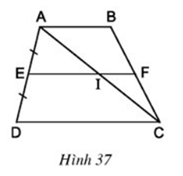
Lời giải

Áp dụng định lí 1 đường trung bình của tam giác

ΔADC có E là trung điểm AD và EI song song với cạnh DC

⇒ Điểm I là trung điểm AC

ΔABC có I là trung điểm AC và FI song song với cạnh AB

⇒ điểm F là trung điểm BC

Câu hỏi 5 trang 79 Toán 8 Tập 1: Tính x trên hình 40.

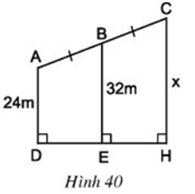
Lời giải

Dựa vào hình vẽ ta thấy rằng AD ⊥ DH, CH ⊥ DH, BE ⊥ DH

Suy ra, AD // BE // CH

Xét tứ giác ADHC có: AC // CH nên ADHC là hình thang.

Ta lại có B là trung điểm của AC và BE // AD // CH

$\Rightarrow$E là trung điểm của BH

Suy ra BE là đường trung bình của hình thang ADHC.

$\begin{array}{l}\Rightarrow BE=\frac{AD+CH}{2}\\ \iff 32=\frac{24+x}{2}\\ \iff 32.2=24+x\\ \iff 64=24+x\\ \iff x=64-24=40.\end{array}$

Bài tập (trang 79, 80)

Bài 20 trang 79 Toán 8 Tập 1:Tính x trên hình 41.

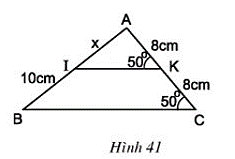
Lời giải

Ta có: $\widehat{AKI}=\widehat{C}=50°$

Mà hai góc ở vị trí hai góc đồng vị

⇒ IK // BC

Ta lại có KA = KC (= 8cm) nên K là trung điểm AC

Xét tam giác ABC, có:

Đường thẳng IK đi qua trung điểm cạnh AC và song song với cạnh BC nên đi qua trung điểm cạnh AB

⇒ I là trung điểm AB

⇒ IA = IB = 10cm hay x = 10cm.

Bài 21 trang 79 Toán 8 Tập 1: Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết rằng C là trung điểm của OA, D là trung điểm của OB và CD = 3cm.

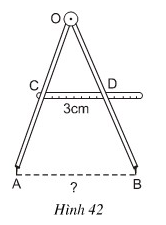
Lời giải

Xét $\Delta OAB$, ta có:

C là trung điểm của OA

D là trung điểm của OB

⇒ CD là đường trung bình của ΔOAB

⇒ $CD=\frac{1}{2}AB$.

⇒ AB = 2CD = 2.3 = 6cm.

Vậy AB = 6cm.

Bài 22 trang 80 Toán 8 Tập 1: Cho hình 43. Chứng minh rằng AI = IM.

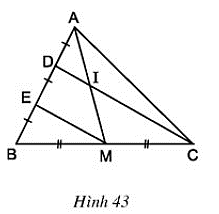
Lời giải

ΔBDC có

BE = ED nên E là trung điểm của BD

BM = CM nên M là trung điểm của BC

⇒ EM là đường trung bình của ΔBDC

⇒ EM // DC hay EM // DI.

ΔAEM có DI // EM (cmt) và AD = DE (gt)

⇒ IA = IM (Theo định lý 1)

Bài 23 trang 80 Toán 8 Tập 1: Tìm x trên hình 44.

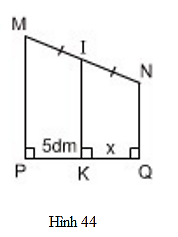
Lời giải

Ta có:

$\left.\begin{array}{l}MP\perp PQ\\ IK\perp PQ\\ NQ\perp PQ\end{array}\right\}\Rightarrow MP//IK//NQ$

Xét tứ giác MNQP, có: MP // NQ

$\Rightarrow$ Tứ giác MPQN là hình thang

Do đường thẳng IK đi qua trung điểm cạnh bên MN và song song với hai đáy nên K là trung điểm PQ.

Nên PK = KQ =5dm

Vậy x = 5dm

Bài 24 trang 80 Toán 8 Tập 1: Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.

Lời giải

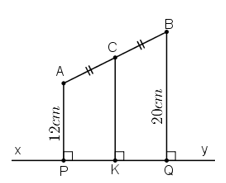
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.

Ta có: $\left.\begin{array}{l}AP\perp xy\\ CK\perp xy\\ BQ\perp xy\end{array}\right\}\Rightarrow AP//CK//BQ$

Xét tứ giác ABQP có AP // BQ

⇒ Tứ giác ABQP là hình thang.

Hình thang ABQP có:

AC = CB (gt) và CK // AP // BQ

⇒ PK = KQ

⇒ CK là đường trung bình của hình thang

⇒ $CK=\frac{AP+BQ}{2}$.

Mà AP = 12cm, BQ = 20cm

$CK=\frac{12+20}{2}=\frac{32}{2}=16cm.$

Vậy khoảng cách từ trung điểm C của AB đến xy bằng CK và bằng: 16cm.

Bài 25 trang 80 Toán 8 Tập 1: Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.

Lời giải

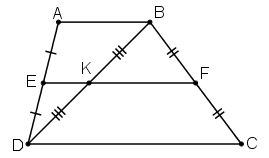
Xét ΔABD có:

D là trung điểm AB

K là trung điểm BD

⇒ EK là đường trung bình của ΔDAB

⇒ EK // AB

Xét hình thang ABCD có:

E là trung điểm của AB

F là trung điểm của BC

⇒ EF là đường trung bình của hình thang ABCD

⇒ EF // AB// CD

Qua điểm E ta có EK // AB và EF // AB nên theo tiên đề Ơclit ta có E, K, F thẳng hàng.

Bài 26 trang 80 Toán 8 Tập 1:Tính x, y trên hình 45 trong đó AB // CD // EF // GH.

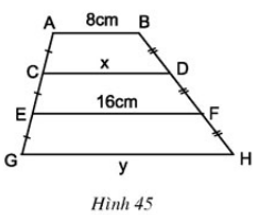
Lời giải

+) Tính x:

Xét tứ giác ABFE, có: AB // EF nên tứ giác ABFE là hình thang

Hình thang ABFE có:

CA = CE nên C là trung điểm của AE

DB = DF nên D là trung điểm của BF

⇒ CD là đường trung bình của hình thang ABFE

$\Rightarrow CD=\frac{AB+\text{EF}}{2}\Rightarrow CD=\frac{8+16}{2}=\frac{24}{2}=12cm.$

+ Tính y:

Vì CD // GH nên tứ giác CDHG là hình thang

Hình thang CDHG có:

EC = EG nên E là trung điểm của CG

FD = FH nên F là trung điểm của DH

⇒ EF là đường trung bình của hình thang CDHG

$\Rightarrow FE=\frac{CD+GH}{2}=\frac{12+y}{2}$

Mà EF = 16cm $\Rightarrow 16=\frac{CD+GH}{2}=\frac{12+y}{2}$

$\begin{array}{l}\Rightarrow 16.2=12+y\\ \Rightarrow 32=12+y\\ \Rightarrow y=32-12=20cm.\end{array}$

Vậy x = 12cm và y = 20cm.

Bài 27 trang 80 Toán 8 Tập 1: Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.

a) So sánh các độ dài EK và CD, KF và AB

b) Chứng minh rằng $\text{EF}\le \frac{AB+CD}{2}.$

Lời giải

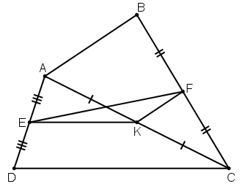
a) + Xét ΔADC có:

E là trung điểm của AD

K là trung điểm của AC

⇒ EK là đường trung bình của ΔADC

$\Rightarrow EK=\frac{CD}{2}$

+ Xét ΔABC có:

K là trung điểm AC

F là trung điểm BC

⇒ KF là đường trung bình của ΔABC

$\Rightarrow KF=\frac{AB}{2}.$

b) Xét $\Delta FEK$, có: EF < EK + KF (Bất đẳng thức tam giác)

Hơn nữa nếu EF = EK + KF

$\iff$ E, K, F thẳng hàng $\iff$AB // CD.

Do đó: EF ≤ EK + KF

Bài 28 trang 80 Toán 8 Tập 1: Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, cắt AC ở K.

a) Chứng minh rằng AK = KC, BI = ID.

b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK.

Lời giải

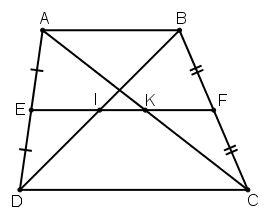
a) + Xét hình thang ABCD có:

E là trung điểm của AD (gt)

F là trung điểm của BC (gt)

⇒ EF là đường trung bình của hình thang ABCD.

⇒ EF // AB // CD

+ Xét ΔABC có:

F là trung điểm BC (gt)

FK // AB (cmt)

⇒ K là trung điểm của AC hay AK = KC.

+ Xét ΔABD có:

E là trung điểm của AD (gt)

EI // AB (cmt)

⇒ I là trung điểm của BD hay BI = ID

b) + Xét hình thang ABCD có:

EF là đường trung bình của hình thang ABCD.

$\Rightarrow EF=\frac{AB+CD}{2}=\frac{6+10}{2}=\frac{16}{2}=8cm$

+ Xét ΔABD có:

FK là đường trung bình của tam giác ABC

⇒ $FK=\frac{1}{2}AB=\frac{1}{2}.6=3cm.$

+ Xét ΔABD có:

EI là đường trung bình của tam giác ABD

$\Rightarrow EI=\frac{1}{2}AB=\frac{1}{2}.6=3cm.$

Mặt khác: FK + IK + IE = EF

$\Rightarrow$IK = EF – FK – IE

$\Rightarrow$IK = 8 – 3 – 3 = 2 cm.