Giải SGK Toán 8 Bài 3: Tính chất đường phân giác của tam giác

Giải bài tập Toán lớp 8 Bài 3: Tính chất đường phân giác của tam giác

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 65 Toán 8 Tập 2: Vẽ tam giác ABC, biết:

AB = 3cm; AC = 6cm; $\widehat{A}$= 100^o.

Dựng đường phân giác AD của góc A (bằng compa, thước thẳng), đo độ dài các đoạn thẳng DB, DC rồi so sánh các tỉ số  $\frac{AB}{AC};\frac{DB}{DC}$ (h.20).

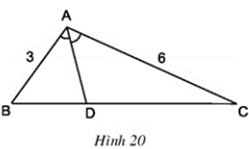
Lời giải:

Dùng thước đo độ dài ta được: BD ≈ 2 cm; DC ≈ 4 cm

Suy ra:

$\begin{array}{l}\frac{AB}{AC}=\frac{3}{6}=\frac{1}{2};\frac{BD}{DC}=\frac{2}{4}=\frac{1}{2}\\ \Rightarrow \frac{AB}{AC}=\frac{BD}{DC}\end{array}$

Câu hỏi 2 trang 67 Toán 8 Tập 2: Xem hình 23a.

a) Tính $\frac{x}{y}$ .

b) Tính x khi y = 5.

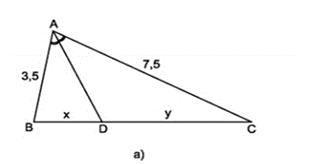
Hình 23

Lời giải:

a) Dựa vào tính chất đường phân giác của tam giác, ta có

$\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow \frac{3,5}{7,5}=\frac{x}{y}\Rightarrow \frac{x}{y}=\frac{7}{15}$

b) Khi y = 5 thì:

$\frac{x}{5}=\frac{7}{15}\Rightarrow x=\frac{7.5}{15}=\frac{7}{3}$

Câu hỏi 3 trang 67 Toán 8 Tập 2: Tính x trong hình 23b.

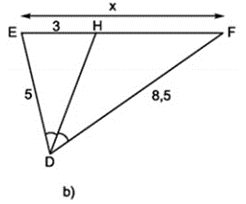
Hình  23

Lời giải:

Dựa vào tính chất đường phân giác của tam giác, ta có

$\begin{array}{l}\frac{DE}{DF}=\frac{EH}{FH}\\ \Rightarrow \frac{5}{8,5}=\frac{3}{FH}\Rightarrow FH=\frac{3.8,5}{5}=5,1\end{array}$

⇒ x = EF = EH + HF = 3 + 5,1 = 8,1

Vậy x = 8,1.

Bài tập (trang 67; 68)

Bài 15 trang 67 Toán 8 Tập 2: Tính x trong hình 24 và làm tròn kết quả đến chữ số thập phân thứ nhất.

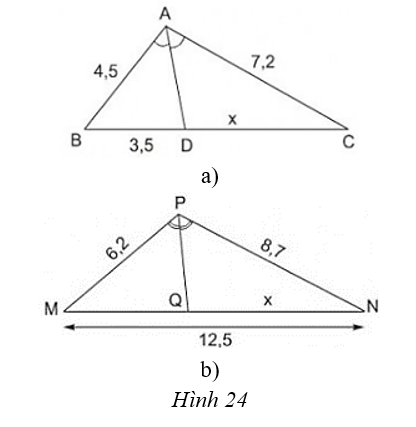
Lời giải:

Áp dụng tính chất đường phân giác trong các tam giác ta có:

a) ΔABC có AD là đường phân giác:

$\frac{DB}{DC}=\frac{AB}{AC}$

Thay số: 

$\frac{3,5}{x}=\frac{4,5}{7,2}\Rightarrow x=\frac{3,5.7,2}{4,5}=5,6$

b) Ta có: MQ + QN = MN nên

MQ = MN – QN = 12,5 – x

ΔPMN có PQ là phân giác nên: 

$\frac{MQ}{QN}=\frac{PM}{PN}$

Thay số:

 $\frac{12,5-x}{x}=\frac{6,2}{8,7}$

⇔ 8,7.(12,5 – x) = x.6,2

⇔ 108,75 – 8,7.x = 6,2.x

⇔ 108,75 = 14,9x

Hay 14,9.x = 108,75

⇔ x ≈ 7,3.

Bài 16 trang 67 Toán 8 Tập 2: Tam giác ABC có độ dài các cạnh AB = m, AC = n và AD là đường phân giác. Chứng minh rằng tỉ số diện tích của tam giác ABD và diện tích của tam giác ACD bằng $\frac{m}{n}$.

Lời giải:

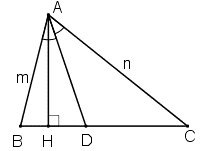
Kẻ AH là đường cao của tam giác ABC

Ta có:

$S_{ABD}=\frac{1}{2}AH.BD;S_{ADC}=\frac{1}{2}AH.CD\Rightarrow \frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.CD}=\frac{BD}{CD}\left(1\right)$

Vì tam giác ABC có AD là đường phân giác nên:

$\frac{BD}{CD}=\frac{AB}{AC}$(2)

Từ (1) và (2) suy ra:

 $\frac{S_{ABD}}{S_{ACD}}=\frac{AB}{AC}=\frac{m}{n}$

Vậy tỉ số diện tích của tam giác ABD và tam giác ACD bằng $\frac{m}{n}$.

Bài 17 trang 68 Toán 8 Tập 2: Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC (h.25).

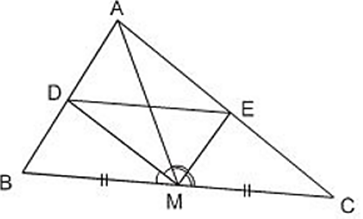
Hình 25

Lời giải:

Ta có: MD là đường phân giác của tam giác ABM nên:

$\frac{AD}{BD}=\frac{AM}{BM}\left(1\right)$.

ME là đường phân giác của tam giác ACM nên:

$\frac{AE}{CE}=\frac{AM}{MC}$  (2)

Mà M là trung điểm BC nên MB = MC. Suy ra: 

$\frac{AM}{BM}=\frac{AM}{MC}\left(3\right)$

Từ (1); (2); (3) suy ra:

 $\frac{AD}{BD}=\frac{AE}{CE}$

Suy ra: DE // BC ( định lí Ta- let đảo).

Bài 18 trang 68 Toán 8 Tập 2: Tam giác ABC có AB = 5cm, AC = 6cm và BC = 7cm. Tia phân giác của góc BAC cắt cạnh BC tại E. Tính các đoạn EB, EC.

Lời giải:

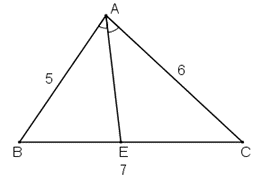
Do AE là đường phân giác của tam giác ABC nên:

$\frac{AB}{AC}=\frac{BE}{EC}\Rightarrow \frac{EC}{AC}=\frac{BE}{AB}$( tính chất của tỉ lệ thức).

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{EC}{AC}=\frac{BE}{AB}=\frac{EC+\text{\hspace{0.17em}\hspace{0.17em}}BE}{AC+\text{\hspace{0.17em}\hspace{0.17em}}AB}=\frac{BC}{6+\text{\hspace{0.17em}\hspace{0.17em}}5}=\frac{7}{11}$

+ Ta có:

 $\frac{EC}{AC}=\frac{7}{11}\Rightarrow \frac{EC}{6}=\frac{7}{11}\Rightarrow EC=\frac{6.7}{11}=\frac{42}{11}$

Suy ra: 

$EB=BC\text{\hspace{0.17em}\hspace{0.17em}}-EC=7-\frac{42}{11}=\frac{35}{11}$

Bài 19 trang 68 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD).

Đường thẳng a song song với DC, cắt các cạnh AD và BC theo thứ tự tại E và F. Chứng minh rằng:

a) $\frac{AE}{ED}=\frac{BF}{FC}$;

b) $\frac{AE}{AD}=\frac{BF}{BC}$;

c) $\frac{DE}{DA}=\frac{CF}{CB}$.

Lời giải:

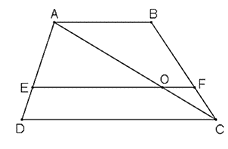
Gọi giao điểm của AC và EF là O.

a) Áp dụng định lí Ta – let ta có:

Tam giác ADC có EO // CD nên

$\frac{AE}{ED}=\frac{AO}{OC}$.(1)

Tam giác ABC có  OF// AB nên

$\frac{AO}{OC}=\frac{BF}{FC}$(2)

Từ (1) (2) suy ra: $\frac{AE}{ED}=\frac{BF}{FC}$.

b) Xét tam giác ADC có EO // CD nên:

$\frac{AE}{AD}=\frac{AO}{AC}$ (3)

Xét tam giác ABC có OF // AB nên

 $\frac{AO}{AC}=\frac{BF}{BC}$  (4)

Từ (3) và (4) suy ra:

$\frac{A\text{}E}{AD}=\frac{BF}{BC}$.

c) Từ câu b ta có:

$\frac{AE}{AD}=\frac{B\text{}F}{BC}\Rightarrow 1-\frac{AE}{AD}=1-\frac{B\text{}F}{BC}\iff \frac{AD-AE}{AD}=\frac{BC-BF}{BC}\iff \frac{DE}{DA}=\frac{CF}{BC}$

Bài 20 trang 68 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F (h.26).

Chứng minh rằng OE = OF

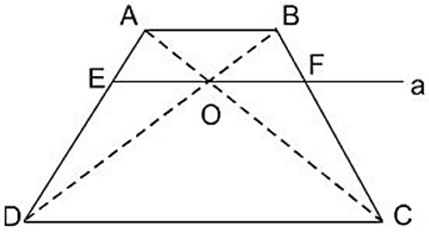
Lời giải:

Xét tam giác ADC có EO // CD nên :

$\frac{OE}{CD}=\frac{AO}{AC}\left(1\right)$ (Hệ quả định lí ta- let).

Xét tam giác BDC có OF // CD nên:

$\frac{OF}{CD}=\frac{BF}{BC}\left(2\right)$  ( hệ quả định lí Ta- let)

Xét tam giác ABC có OF // AB nên theo định lí  Ta – let :

$\frac{AO}{AC}=\frac{BF}{BC}\left(3\right)$

Từ (1); (2); (3) suy ra: 

$\text{}\frac{OE}{CD}=\frac{AO}{AC}=\frac{BF}{BC}=\frac{OF}{CD}$

$\Rightarrow OE=OF$ (đpcm)

Bài 21 trang 68 Toán 8 Tập 2: a) Cho tam giác ABC với đường trung tuyến AM và đường phân giác trong AD. Tính diện tích tam giác ADM, biết AB = m, AC = n (n > m) và diện tích tam giác ABC là S.

b) Khi cho n = 7cm, m = 3cm, hỏi rằng diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC?

Lời giải:

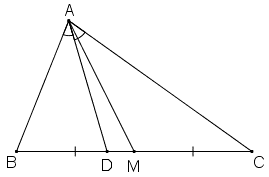
a) Ta có: $\frac{S_{ABD}}{S_{ABC}}=\frac{BD}{BC}$  (do hai tam giác có chung chiều cao từ đỉnh A)  (1)

ΔABC có AD là phân giác nên:

 $\frac{CD}{BD}=\frac{AC}{AB}$ (tính chất đường phân giác).

Suy ra:

 $\frac{CD}{BD}+\text{\hspace{0.17em}}1=\frac{AC}{AB}+\text{\hspace{0.17em}\hspace{0.17em}}1$

$\Rightarrow \frac{CD+BD}{BD}=\frac{AC\text{\hspace{0.17em}\hspace{0.17em}}+AB}{AB}\iff \frac{BC}{BD}=\frac{AB+AC}{AB}$

$\iff \frac{BD}{BC}=\frac{AB}{AB+\text{\hspace{0.17em}\hspace{0.17em}}AC}$ (2)

Từ (1) (2) suy ra:

$\frac{S_{ABD}}{S_{ABC}}=\frac{AB}{AB+\text{\hspace{0.17em}\hspace{0.17em}}AC}$.

Hay $S_{ABD}=\frac{m}{m+n}S$.

Lại có:

 $\frac{S_{ABM}}{S_{ABC}}=\frac{BM}{BC}=\frac{1}{2}\Rightarrow S_{ABM}=\frac{1}{2}{S}_{ABC}$

Do đó, 

$S_{ADM}=S_{ABM}-S_{ABD}=\frac{1}{2}S-\frac{m}{m+\text{\hspace{0.17em}}n}S=\frac{n-m}{2(m+n)}S$

b) Với n = 7; m = 3, thay vào kết quả phần a ta có:

$S_{ADM}=\frac{7-3}{2(7+\text{}3)}S=\frac{4}{20}S=\frac{1}{5}S=20\%.S$

Vậy diện tích tam giác ADM chiếm 20% diện tích tam giác ABC.

Bài 22 trang 68 Toán 8 Tập 2: Đố: Hình 27 cho biết có 6 góc bằng nhau:

$\widehat{O_1}=\widehat{O_2}=\widehat{O_3}=\widehat{O_4}=\widehat{O_5}=\widehat{O_6}$

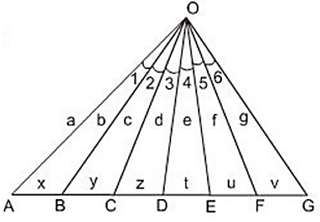
Hình 27

Kích thước các đoạn thẳng đã được ghi trên hình. Hãy thiết lập những giá trị từ các kích thước đã cho.

Lời giải:

Theo tính chất đường phân giác trong tam giác ta có:

OB là tia phân giác của tam giác OAC nên $\frac{x}{a}=\frac{y}{c}$.

OC là tia phân giác của tam giác BOD nên $\frac{y}{b}=\frac{z}{d}$

OD là tia phân giác của tam giác OCE nên $\frac{z}{c}=\frac{t}{e}$

OE là tia phân giác của tam giác ODF nên $\frac{t}{d}=\frac{u}{f}$

OF là tia phân giác của tam giác OEG nên $\frac{u}{e}=\frac{v}{g}$

OC là tia phân giác của tam giác OAE nên

 $\frac{AC}{OA}=\frac{CE}{OE}\Rightarrow \frac{x+y}{a}=\frac{z+t}{e}$

OE là tia phân giác của tam giác OCG nên

 $\frac{z+t}{c}=\frac{u+v}{g}$

OD là tia phân giác của tam giác AOG nên

 $\frac{x+\text{\hspace{0.17em}}y+z}{a}=\frac{t+u+\text{\hspace{0.17em}}v}{g}$

OD là tia phân giác của tam giác OBF nên

$\frac{y+\text{\hspace{0.17em}}z}{b}=\frac{t+u}{f}$.