Tài liệu Định lí Ta-lét trong tam giác gồm các nội dung chính sau:
A. Lý thuyết
– tóm tắt lý thuyết ngắn gọn.
B. Các dạng bài tập
– gồm 3 dạng bài tập vận dụng có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng bài tập Định lí Ta-lét trong tam giác.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

ĐỊNH LÍ TA – LÉT TRONG TAM GIÁC
A. Lý thuyết
- Tỉ số của hai đoạn thẳng. Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
- Đoạn thẳng tỉ lệ. Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B và C’D nếu có tỉ lệ thức:
hay
- Định lý Ta-let trong tam giác. Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Trong hình bên
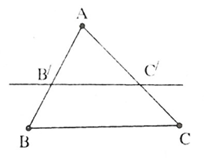
1. Định lý Ta-lét đảo. Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Trong hình bên
2. Hệ quả của định lý Ta-lét. Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Trong hình bên:
Chú ý. Hệ quả trên vẫn đúng cho trường hợp đường thẳng a song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.
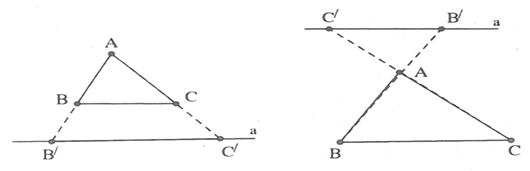
B. Các dạng bài tập
Dạng 1. Tỉ số của hai đoạn thẳng
Ví dụ 1: 1. Với và thì ta có tỉ số của nó là
2. Với và thì ta có tỉ số của nó là
Định nghĩa: Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
F Chú ý: Tỉ số của hai đoạn thẳng không phu thuộc vào cách chọn đơn vị đo.
Dựa vào tỉ số của hai đoạn thẳng chúng ta có thể tính được độ dài của đoạn thẳng, thí dụ sau minh hoạ điều này.
Ví dụ 2: Cho đoạn thẳng . Trên đường thẳng AB lấy các điểm C, D sao cho (C nằm trong đoạn thẳng AB, D nằm ngoài đoạn thẳng AB). Tính độ dài các đoạn thẳng CA, DA.
Xem thêm