Bất phương trình dạng tích, thương

Tài liệu Bất phương trình dạng tích, thương gồm các nội dung sau:

I. Phương pháp giải

– Tóm tắt lý thuyết ngắn gọn

II. Một số ví dụ

– Gồm 9 ví dụ minh họa đa dạng cho dạng bài Bất phương trình dạng tích, thương có lời giải chi tiết

III. Bài tập vận dụng

– Gồm 17 bài tập vận dụng có lời giải chi tiết giúp học sinh rèn luyện cách giải các bài tập Bất phương trình dạng tích, thương

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

BẤT PHƯƠNG TRÌNH DẠNG TÍCH, THƯƠNG

I. Phương pháp giải

1. Bất phương trình dạng tích:$A\left(x\right).B\left(x\right)>0$ ;

                             (hoặc $A\left(x\right).B\left(x\right)<0;A\left(x\right).B\left(x\right)\ge 0;A\left(x\right).B\left(x\right)\le 0$);

2. Bất phương trình dạng thương: $\frac{A\left(x\right)}{B\left(x\right)}>0$

                                      (hoặc $\frac{A\left(x\right)}{B\left(x\right)}<0;\frac{A\left(x\right)}{B\left(x\right)}\ge 0;\frac{A\left(x\right)}{B\left(x\right)}\le 0$).

3. Định lý về dấu của nhị thức bậc nhất $ax+b(a\ne 0)$:

Nhị thức bậc nhất cùng dấu với a khi $x>–\frac{b}{a}$

Nhị thức bậc nhất trái dấu với a khi $x<–\frac{b}{a}$

Do $–\frac{b}{a}$ là nghiệm của nhị thức $ax+b$ nên định lý được phát biểu:

Nhị thức $ax+b(a\ne 0)$ cùng dấu với a với các giá trị của x lớn hơn nghiệm của nhị thức, trái dấu với a với các giá trị của x nhỏ hơn nghiệm của nhị thức.

4. Phương pháp giải các bất phương trình dạng tích, thương: Phân tích thành nhân tử chứa các nhị thức bậc nhất. Lập bảng xét dấu của nhị thức bậc nhất $ax+b$

$x$		$–\frac{b}{a}$
$ax+b$	trái dấu với a	0	cùng dấu với a

II. Một số ví dụ

Ví dụ 1: Giải bất phương trình $(2x–9)(1945+x)>0$.

Tìm cách giải: Với tích $A.B>0$ xảy ra khi A và B cùng dấu. Do đó $A>0$ và $B>0$ hoặc $A<0$ và $B<0$. Ta có cách giải:

Giải

Cách 1: Bất phương trình đã cho tương đương với:

\[\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}2x – 9 > 0\\1945 + x > 0\end{array} \right.\\\left\{ \begin{array}{l}2x – 9 < 0\\1945 + x < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}2x > 9\\x >  – 1945\end{array} \right.\\\left\{ \begin{array}{l}2x < 9\\x <  – 1945\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 4,5\\x >  – 1945\end{array} \right.\\\left\{ \begin{array}{l}x < 4,5\\x <  – 1945\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 4,5\\x <  – 1945\end{array} \right.\end{array}\]

Vậy nghiệm của bất phương trình là \[x > 4,5;{\rm{ }}x <  – 1945\].

* Chú ý: Bằng việc lập bảng xét dấu của từng thừa số của tích là nhị thức bậc nhất ta có cách 2: Lập bảng xét dấu:

\[x\]		\[ – 1945\]		4,5
\[2x – 9\]	–	0	–	|	+
\[1945 + x\]	–	|	+	0	+
\[\left( {2x – 9} \right)\left( {1945 + x} \right)\]	+	0	–	0	+

Vậy nghiệm của bất phương trình: \[x > 4,5\] hoặc \[x <  – 1945\].

Ví dụ 2: Giải bất phương trình \[\left( {x – 6} \right)\left( {x + 10} \right) <  – {x^2} + x + 30\].

* Tìm cách giải: Ta phân tích vế phải thành nhân tử, xuất hiện nhân tử chung và chuyển vế để đưa về phương trình tích.

Giải

a)     Ta có:

 \[\begin{array}{l} – {x^2} + x + 30\\ =  – {x^2} + 6x – 5x + 30\\ =  – \left( {x – 6} \right)\left( {x + 5} \right)\end{array}\]

Do đó bất phương trình thành \[\left( {x – 6} \right)\left( {x + 10} \right) + \left( {x – 6} \right)\left( {x + 5} \right) < 0\]

\[ \Leftrightarrow \left( {x – 6} \right)\left( {2x + 15} \right) < 0\]. Lập bảng xét dấu:

\[x\]		\[ – 7,5\]		6
\[x – 6\]	–	|	–	0	+
\[2x + 15\]	–	0	+	|	+
\[\left( {x – 6} \right)\left( {2x + 15} \right)\]	+	0	–	0	+

Nghiệm của bất phương trình là: \[ – 7,5 < x < 6\].

Ví dụ 3: Giải bất phương trình \[{x^4} + 36 \ge 13{x^2}\] sau đó biểu diễn nghiệm trên trục số.

* Tìm cách giải: Chuyển tất cả về một vế rồi phân tích vế đó thành nhân tử và giải bất phương trình tích.

Giải

Ta có \[{x^4} + 36 \ge 13{x^2} \Leftrightarrow {x^4} – 13{x^2} + 36 \ge 0\]

\[\begin{array}{l} \Leftrightarrow {x^4} – 9{x^2} – 4{x^2} + 36 \ge 0\\ \Leftrightarrow \left( {{x^2} – 9} \right)\left( {{x^2} – 4} \right) \ge 0\end{array}\]

\[ \Leftrightarrow \left( {x – 2} \right)\left( {x + 2} \right)\left( {x – 3} \right)\left( {x + 3} \right) \ge 0\]. Lập bảng xét dấu:

\[x\]		\[ – 3\]		\[ – 2\]		2		3
\[x – 2\]	–	|	–	|	–	0	+	|	+
\[x + 2\]	–	|	–	0	+	|	+	|	+
\[x – 3\]	–	|	–	|	–	|	–	0	+
\[x + 3\]	–	0	+	|	+	|	+	|	+
Vế trái	+	0	–	0	+	0	–	0	+

Nghiệm của bất phương trình là: \[\left[ \begin{array}{l}x \le  – 3\\ – 2 \le x \le 2\\x \ge 3\end{array} \right.\]. Biểu diễn nghiệm:

Ví dụ 4: Giải bất phương trình: \[\frac{{2016 – 6x}}{{x\left( {x + 8} \right)}} \le 0\].

* Tìm cách giải: Đây là bất phương trình dạng thương của \[\left( {2016 – 6x} \right)\] chia cho \[x\left( {x – 8} \right)\].

Ta có:

 \[\begin{array}{l}2016 – 6x = 0 \Leftrightarrow x = 336;\\{\rm{ }}x + 8 = 0 \Leftrightarrow x =  – 8\end{array}\].

Giải

ĐKXĐ: \[x \ne 0\] và \[x \ne  – 8\]. Đặt \[A = \frac{{2016 – 6x}}{{x\left( {x + 8} \right)}}\]. Lập bảng xét dấu:

\[x\]		\[ – 8\]		0		336
\[2016 – 6x\]	+	|	+	|	+	0	–
\[x\]	–	|	–	0	+	|	+
\[x + 8\]	–	0	+	|	+	|	+
A	+	||	–	||	+	0	–

\[A \le 0\] khi \[\left[ \begin{array}{l} – 8 < x < 0\\x \ge 336\end{array} \right.\].

Ví dụ 5: Giải bất phương trình \[\frac{{ – {x^2} – 5x + 28}}{{{x^2} + 2x – 15}} \ge  – 2{\rm{          }}\left( 1 \right)\]

Và biểu diễn nghiệm trên trục số.

* Tìm cách giải: Nếu chuyển vế, rút gọn vế trái ta được bất phương trình dạng thương. Phân tích các tử, mẫu thành nhân tử rồi lập bảng xét dấu.

Giải

ĐKXĐ: \[x \ne 3;{\rm{ }}x \ne  – 5\]

\[\begin{array}{l}\left( 1 \right) \Leftrightarrow \frac{{ – {x^2} – 5x + 28}}{{{x^2} + 2x – 15}} + 2 \ge 0\\ \Leftrightarrow \frac{{{x^2} – x – 2}}{{{x^2} + 2x – 15}} \ge 0\\ \Leftrightarrow \frac{{\left( {x + 1} \right)\left( {x – 2} \right)}}{{\left( {x – 3} \right)\left( {x + 5} \right)}} \ge 0\end{array}\]

Lập bảng xét dấu ta có:

\[x\]		\[ – 5\]		\[ – 1\]		2		3
\[x + 1\]	–	|	–	0	+	|	+	|	+
\[x – 2\]	–	|	–	|	–	0	+	|	+
\[x – 3\]	–	|	–	|	–	|	–	0	+
\[x + 5\]	–	0	+	|	+	|	+	|	+
Vế trái	+	||	–	0	+	0	–	||	+

Nghiệm của bất phương trình là \[\left[ \begin{array}{l}x <  – 5\\ – 1 \le x \le 2\\x > 3\end{array} \right.\]. Biểu diễn nghiệm:

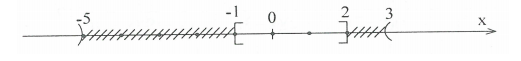
Ví dụ 6: Cho biểu thức \[A = \left[ {\frac{5}{{x + 3}} – \frac{{5x – 15}}{{2x – 9}}.\left( {\frac{{2x – 9}}{{{x^2} – 9}} – 2x + 9} \right)} \right]:\frac{{1 – x}}{{1 + x}}\].

Tìm x để \[A < 0\]

* Tìm cách giải: Khi rút gọn biểu thức và khi tìm x để \[A < 0\] cần lưu ý ĐKXĐ. Do sau khi chia \[1 – x\] cũng thành mẫu số nên \[x \ne  \pm 1\].

Giải

Rút gọn A: ĐKXĐ: \[x \ne  \pm 3;{\rm{ }}x \ne  \pm 1;{\rm{ }}x \ne 4,5\]. Ta có:

\[A = \left[ {\frac{5}{{x + 3}} – \frac{{5\left( {x – 3} \right)}}{{\left( {2x – 9} \right)}}.\frac{{\left( {2x – 9} \right)\left( {1 – {x^2} + 9} \right)}}{{\left( {x – 3} \right)\left( {x + 3} \right)}}} \right].\frac{{1 + x}}{{1 – x}}\]

    \[\begin{array}{l} = \left[ {\frac{5}{{x + 3}} – \frac{{5\left( {1 – {x^2} + 9} \right)}}{{x + 3}}} \right].\frac{{1 + x}}{{1 – x}}\\ = \frac{{5\left( {x – 3} \right)\left( {x + 3} \right)}}{{x + 3}}.\frac{{1 + x}}{{1 – x}}\\ = \frac{{5\left( {x – 3} \right)\left( {1 + x} \right)}}{{1 – x}}\end{array}\]

Lập bảng xét dấu:

\[x\]		\[ – 1\]		1		3
\[x – 3\]	–	|	–	|	–	0	+
\[1 + x\]	–	0	+	|	+	|	+
\[1 – x\]	+	|	+	0	–	|	–
A	+	||	–	||	+	||	–

Vậy để \[A < 0\] thì \[\left[ \begin{array}{l} – 1 < x < 1\\x > 3;x \ne 4,5\end{array} \right.\].

Ví dụ 7: Giải bất phương trình:

                   \[\frac{1}{{{x^2} – x}} + \frac{1}{{{x^2} – 3x + 2}} + \frac{1}{{{x^2} – 5x + 6}} + … + \frac{1}{{{x^2} – 39x + 380}} < 0\].

* Tìm cách giải: Bất phương trình có ẩn ở mẫu nên lưu ý ĐKXĐ.

Ta có \[{x^2} – x = x\left( {x – 1} \right);{\rm{ }}{x^2} – 3x + 2 = \left( {x – 1} \right)\left( {x – 2} \right);…\] có dạng tổng quát \[A.\left( {A – 1} \right)\].

Mà \[\frac{1}{{A\left( {A – 1} \right)}} = \frac{{A – \left( {A – 1} \right)}}{{A\left( {A – 1} \right)}} = \frac{1}{{A – 1}} – \frac{1}{A}\]. Ta phân tích các phân thức ở vế trái rồi rút gọn, sẽ được một phân thức dạng thương.

Giải

ĐKXĐ: \[x \notin \left\{ {0;1;2;3;….;19;20} \right\}\].

Biến đổi bất đẳng thức thành:

\[\frac{1}{{x\left( {x – 1} \right)}} + \frac{1}{{\left( {x – 1} \right)\left( {x – 2} \right)}} + \frac{1}{{\left( {x – 2} \right)\left( {x – 3} \right)}} + … + \frac{1}{{\left( {x – 19} \right)\left( {x – 20} \right)}} < 0\]

\[ \Leftrightarrow \frac{1}{{x – 1}} – \frac{1}{x} + \frac{1}{{x – 2}} – \frac{1}{{x – 1}} + … + \frac{1}{{x – 20}} – \frac{1}{{x – 19}} < 0\]

\[ \Leftrightarrow \frac{1}{{x – 20}} – \frac{1}{x} < 0 \Leftrightarrow \frac{{20}}{{x\left( {x – 20} \right)}} < 0\].

Đặt \[A = \frac{{20}}{{x\left( {x – 20} \right)}}\]. Lập bảng xét dấu

\[x\]		0		20
\[x\]	–	0	+	|	+
\[x – 20\]	–	|	–	0	+
\[A\]	+	||	–	||	+

 

\[A < 0\] khi \[x \notin \left\{ {1;2;3;…;19} \right\}\]và \[0 < x < 20\].

Ví dụ 8: Giải bất phương trình \[\frac{{m – 5}}{{x – 2}} > 3\] với m là tham số.

* Tìm cách giải: Bất phương trình có ẩn ở mẫu là có tham số nên phải lưu ý ĐKXĐ và biện luận tham số m khi giải bất phương trình.

Giải

ĐKXĐ: \[x \ne 2\]

\[\frac{{m – 5}}{{x – 2}} > 3 \Leftrightarrow \frac{{m – 5}}{{x – 2}} – 3 > 0 \Leftrightarrow \frac{{\left( {m + 1} \right) – 3x}}{{x – 2}} > 0\]

Ta thấy \[m + 1 – 3x = 0 \Leftrightarrow x = \frac{{m + 1}}{3}\].

Ta có \[\frac{{m + 1}}{3} > 2 \Leftrightarrow m > 5\] và \[\frac{{m + 1}}{3} < 2 \Leftrightarrow m < 5\].

Đặt \[B = \frac{{\left( {m + 1} \right) – 3x}}{{x – 2}}\].

Lập bảng xét dấu: khi \[m > 5\]

\[x\]		2		\[\frac{{m + 1}}{3}\]
\[m + 1 – 3x\]	+	|	+	0	–
\[x – 2\]	–	0	+	|	+
\[B\]	–	||	+	0	–

Với \[m > 5\] ta có nghiệm của bất phương trình là: \[2 < x < \frac{{m + 1}}{3}\].

 

Lập bảng xét dấu: khi \[m < 5\]

\[x\]		\[\frac{{m + 1}}{3}\]		2
\[m + 1 – 3x\]	+	0	–	|	–
\[x – 2\]	–	|	–	0	+
\[B\]	–	0	+	||	–

Với \[m < 5\] ta có nghiệm của bất phương trình là: \[\frac{{m + 1}}{3} < x < 2\]

 

Xem thêm