50 Bài tập Diện tích tam giác (có đáp án)- Toán 8

Bài tập Toán 8 Chương 2 Bài 3: Diện tích tam giác

A. Bài tập Diện tích tam giác

I. Bài tập trắc nghiệm

Bài 1: Cho Δ ABC, có đường cao AH = $\frac{2}{3}$BC thì diện tích tam giác là ?

A. $\frac{2}{5}$BC².   

B. $\frac{2}{3}$BC².

C. $\frac{1}{3}$BC².  

D. $\frac{1}{3}$BC.

Lời giải:

Ta có diện tích của tam giác: S = $\frac{1}{2}$b.h.

Trong đó: b là độ dài cạnh đáy, h là độ dài đường cao

Khi đó ta có : S = $\frac{1}{2}$AH.BC = $\frac{1}{2}$.$\frac{2}{3}$BC.BC = $\frac{1}{3}$BC².

Chọn đáp án C.

Bài 2: Δ ABC có đáy BC = 6cm, đường cao AH = 4cm. Diện tích Δ ABC là ?

A. 24cm²   

B. 12cm²

C. 24cm.   

D. 14cm²

Lời giải:

Ta có diện tích Δ ABC là S = $\frac{1}{2}$AH.BC = $\frac{1}{2}$.6.4 = 12( cm² ).

Chọn đáp án B.

Bài 3: Cho Δ ABC vuông tại A, có đáy BC = 5cm và AB = 4cm. Diện tích Δ ABC là ?

A. 12cm²   

B. 10cm

C. 6cm²   

D. 3cm²

Lời giải:

Áp dụng định lý Py – to – go ta có: AB² + AC² = BC² ⇒ AC = $\sqrt{\left(B{C}^2–A{B}^2\right)}$

⇒ AC = $\sqrt{5^2–4^2}$ = 3cm.

Khi đó S_ABC = $\frac{1}{2}$AB.AC = $\frac{1}{2}$.4.3 = 6( cm² )

Chọn đáp án C.

Bài 4: Cho Δ ABC, đường cao AH. Biết AB = 15cm, AC = 41cm, HB = 12cm. Diện tích của Δ ABC là ?

A. 234 (cm²)   

B. 214 (cm²)

C. 200 (cm²)   

D. 154 (cm²)

Lời giải:

Áp dụng định lý Py – to – go ta có:

+ Xét Δ ABH có AH² + BH² = AB² ⇒ AH = $\sqrt{(A{B}^2 – B{H}^2)}$

⇒ AH = $\sqrt{({15}^2 – {12}^2)}$ = 9 ( cm ).

+ Xét Δ ACH có AC² = AH² + HC² ⇒ HC = $\sqrt{(A{C}^2 – A{H}^2)}$

⇒ HC = $\sqrt{({41}^2 – 9^2)}$ = 40 ( cm ).

Khi đó S_ABC = $\frac{1}{2}$AH.BC = $\frac{1}{2}$AH( HB + HC ) = $\frac{1}{2}$.9.( 12 + 40 ) = 234 ( cm² ).

Chọn đáp án A.

Bài 5: Cho tam giác ABC có AB = 6cm, AC = 8cm. Hai đường cao xuất phát từ đỉnh B và C là BH và CK. Biết BH = 9cm. Tính CK

A. 12cm    

B. 15cm

C. 9cm    

D. 8cm

Lời giải:

Diện tích tam giác ABC là:

Suy ra: 3CK = 36 nên CK = 12cm

Chọn đáp án A

Bài 6: Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8 cm. Tính độ dài đường cao xuất phát từ A?

A. 4cm    

B. 4,5cm

C. 4,8cm    

D. 5cm

Lời giải:

Áp dụng định lí Pytago vào tam giác ABC ta có:

BC² = AB² + AC² = 6² + 8² = 100

Suy ra: BC = 10cm

Diện tích tam giác ABC là:

Gọi AH là đường cao xuất phát từ đỉnh A của tam giác ABC ,

Khi đó:

Suy ra: 5AH = 24 ⇔ AH = 4,8cm

Chọn đáp án C

Bài 7: Cho tam giác ABC có đường cao AH = 6cm, diện tích tam giác ABC là 30 cm². Gọi M là trung điểm của BC. Tính diện tích tam giác ABM

A. 10cm²    

B. 12cm²

C. 20cm²    

D. 15cm²

Lời giải:

Chọn đáp án D

Bài 8: Cho tam giác ABC có diện tích bằng 40cm². Gọi M là trung điểm của AC . Tính diện tích tam giác ABM?

A. 10cm²    

B. 20cm²

C. 25cm²    

D. Chưa thể kết luận

Lời giải:

Chọn đáp án B

Bài 9: Cho tam giác ABC có AB = 4cm và AC = 7cm. Gọi BH và CK theo thứ tự là đường vuông góc từ đỉnh B và C của tam giác. Tính $\frac{BH}{CK}$ ?

A. $\frac{4}{7}$     

B. $\frac{7}{4}$

C. $\frac{4}{3}$    

D. Đáp án khác

Lời giải:

Chọn đáp án A

Bài 10: Cho tam giác ABC có AB = 6cm và AC = 8cm . Gọi M và N theo thứ tự là trung điểm của AC và AB. Tính tỉ số 

A. $\frac{1}{2}$    

B. 2

C. 1    

D. Chưa thể kết luận

Lời giải:

Chọn đáp án C

II. Bài tập tự luận có lời giải

Bài 1: Giải thích vì sao diện tích của tam giác được tô đậm trong hình 128, 129, 130 bằng nửa diện tích hình chữ nhật tương ứng.

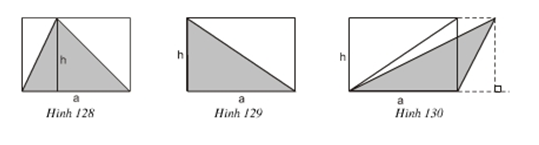
Lời giải:

Trong mỗi hình trên ta đều có:

Diện tích hình chữ nhật là: a.h

⇒ Diện tích của tam giác bằng nửa diện tích hình chữ nhật tương ứng.

Bài 2 Cho tam giác ABC và đường trung tuyến AM (h.132). Chứng minh: S_AMB = S_AMC

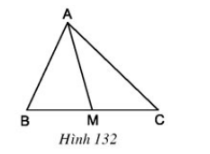
Lời giải:

Kẻ đường cao AH.

Ta có:

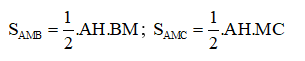
Mà BM = CM (vì AM là trung tuyến)

⇒ S_AMB = S_AMC (đpcm).

Bài 3

a) Xem hình 133. Hãy chỉ ra các tam giác có cùng diện tích (lấy ô vuông làm đơn vị diện tích)

b) Hai tam giác có diện tích bằng nhau thì có bằng nhau hay không?

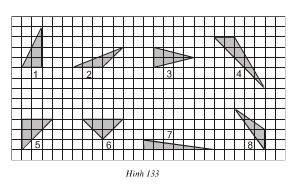
Lời giải:

a) Các tam giác số 1, 3, 6 có cùng diện tích là 4 ô vuông

Các tam giác số 2, 8 có cùng diện tích là 3 ô vuông.

Các tam giác số 4, 5, 7 không có cùng diện tích với các tam giác nào khác (diện tích tam giác số 4 là 5 ô vuông, tam giác số 5 là 4, 5 ô vuông, tam giác số 7 là 3,5 ô vuông).

b) Hai tam giác có diện tích bằng nhau thì không nhất thiết bằng nhau.

Vì diện tích của tam giác là 1 nửa tích của độ dài đáy với chiều cao tương ứng của đáy, nên chỉ cần tích của đáy với chiều cao bằng nhau thì 2 tam giác đó có diện tích bằng nhau, 2 cạnh còn lại có thể khác nhau.

Bài 4 Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135). Hãy chỉ ra:

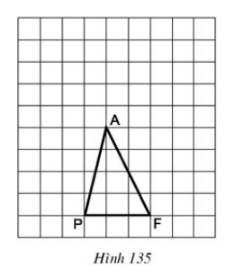
a) Một điểm I sao cho S_PIF= S_PAF

b) Một điểm O sao cho S_POF= 2.S_PAF

c) Một điểm N sao cho:

Lời giải:

Gọi AH là chiều cao của tam giác APF.

Ta có: S_APF = $\frac{AH.PF}{2}$.

a) S_PIF= S_PAF

⇔ chiều cao IK = AH (Chung cạnh đáy PF).

⇔ I nằm trên đường thẳng song song với PF và cách PF 1 khoảng bằng AH.

b) S_POF= 2.S_PAF

⇔ chiều cao OM = 2.AH

⇔ O nằm trên đường thẳng song song với PF và cách PF một khoảng bằng 2.AH

c)

⇔ chiều cao NQ = $\frac{AH}{2}$

⇔ N nằm trên đường thẳng song song với PF và cách PF một khoảng bằng AH/2.

Bài 4 Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135). Hãy chỉ ra:

a) Một điểm I sao cho S_PIF = S_PAF

b) Một điểm O sao cho S_POF = 2.S_PAF

c) Một điểm N sao cho 

Lời giải:

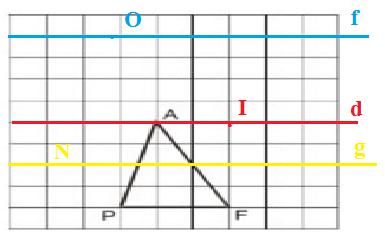
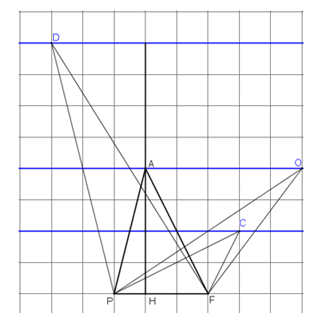
Cho ΔPAF vẽ trên giấy kẻ ô vuông như trên hình.

a) Nếu lấy điểm I bất kì nằm trên đường thẳng d đi qua A và song song với đường thẳng PF thì S_PIF = S_PAF

(cùng bằng nửa tích khoảng cách từ A (hoặc I) đến PF nhân với độ dài của PF)

b) Nếu lấy một điểm O sao cho khoảng cách từ O đến đường thẳng PF bằng hai lần khoảng cách từ A đến đường thẳng PF thì S_POF = 2S_PAF.

Có vô số điểm O như thế (ví dụ O nằm trên đường thẳng f như trên hình).

c) Nếu lấy điểm N sao cho khoảng cách từ N đến đường thẳng PF

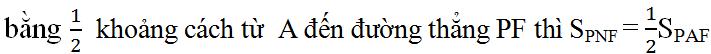
Có vô số điểm N như thế nằm trên hai đường thẳng song song với đường thẳng PF (ví dụ đường thẳng g).

Bài 5 Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M nằm trong tam giác đó sao cho: S_AMB + S_BMC = S_MAC

Lời giải:

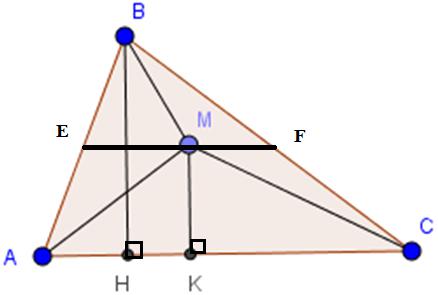
Kẻ đường cao BH, MK.

Theo giả thiết, M là điểm nằm trong tam giác ABC sao cho:

S_AMB + S_BMC = S_MAC

Ta lại có: S_AMB + S_BMC + S_MAC = S_ABC

Suy ra: S_MAC = $\frac{1}{2}$ S_ABC

⇒ $\frac{1}{2}$ MK.AC = $\frac{1}{2}$ ($\frac{1}{2}$ BH.AC)

⇒ MK = $\frac{1}{2}$ BH

Do đó, M nằm trên đường thẳng sao cho khoảng cách từ M đến BC = $\frac{1}{2}$ đường cao BH.

Vậy điểm M nằm trên đường trung bình của ΔABC

Bài 6 Tính diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.

Lời giải:

Gọi h là chiều cao của tam giác cân.

Theo định lí Pitago ta có:

Bài 7 Tính diện tích của một tam giác đều có cạnh bằng a.

Lời giải:

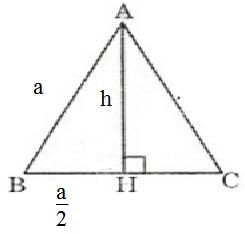
Gọi h là chiều cao của tam giác đều cạnh a.

Theo định lí Pitago ta có:

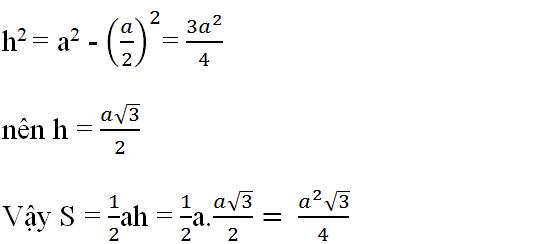
Bài 8 Tính x sao cho diện tích hình chữ nhật. ABCD gấp ba lần diện tích tam giác ADE (h.134).

Lời giải:

Ta có AD = BC = 5cm

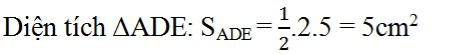
Diện tích hình chữ nhật ABCD: S_ABCD = 5x

Theo đề bài ta có S_ABCD = 3S_ADE nên 5x = 3.5

Vậy x = 3cm

III. Bài tập vận dụng

Bài 1 Cho tam giác ABC có diện tích 150cm². M là trung điểm của BC, N là trung điểm của AC. Nối MN. Tính diện tích tam giác CMN ?

Bài 2 Cho hình vẽ. Tính tỉ số diện tích 2 tam giác BDF và AEF ?

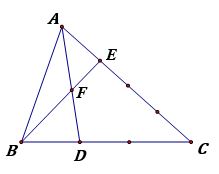
Bài 3 Cho hình chữ nhật ABCD, F là một điểm bất kì trên cạnh AD, BF cắt CD kéo dài tại điểm E. Nối điểm A với điểm E. Tính diện tích tam giác AEF, biết AF = 3cm, BC = 5cm, AB = 7 cm ?

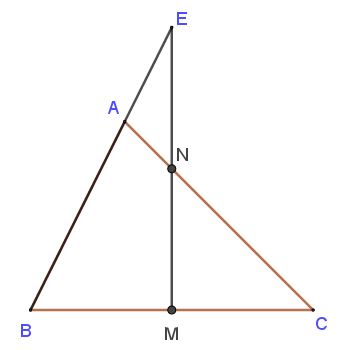
Bài 4 Cho tam giác ABC biết BM = MC; CN = 3 x NA (như hình vẽ) và diện tích tam giác AEN bằng 27 cm².Tính diện tích tam giác ABC ?

Bài 5 Cho hình vẽ bên biết S1 = 12cm². Tính S2

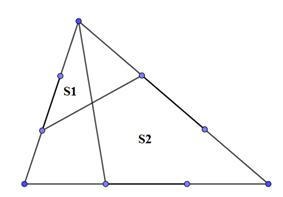
Bài 6 Cho tam giác với các tỷ lệ như hình.

Biết S3−S1=84cm². Tính S4−S2

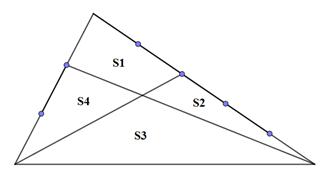
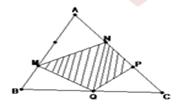
Bài 7 Cho tam giác ABC có diện tích là 180 cm2. Biết AB = 3 x BM; AN = NP=PC; QB=QC. Tính diện tích tam giác MNPQ ? (xem hình vẽ)

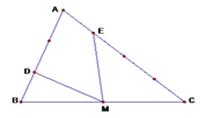
Bài 8 Cho tam giác ABC có diện tích bằng 18cm². Biết DA = 2 x DB ; EC = 3 x EA ; MC = MB (hình vẽ). Tính tổng diện tích hai tam giác MDB và MCE ?

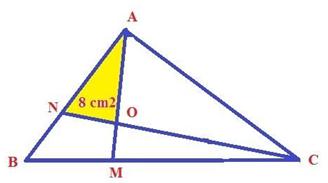
Bài 9 Trong hình vẽ bên có NA = 2 x NB; MC = 2 x MB và diện tích tam giác OAN là 8cm². Tính diện tích BNOM ?

Bài 10 Cho tam giác ABC và các điểm D, E, G, H sao cho BD = $\frac{1}{3}$x AB; AE = CG = $\frac{1}{3}$ x AC; CH =$\frac{1}{3}$x BC. Tính diện tích hình BDEGH ? ( Biết diện tích của tam giác ABC là 180cm² )

B. Lý thuyết Diện tích tam giác

1. Khái niệm diện tích đa giác

• Số đo của phần mặt phẳng giới hạn bởi một đa giác được gọi là diện tích đa giác đó.

• Mỗi đa giác có một diện tích xác định. Diện tích đa giác là một số dương.

• Diện tích đa giác có các tính chất sau:

– Hai tam giác bằng nhau thì có diện tích bằng nhau.

– Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó.

– Nếu chọn hình vuông có cạnh bằng 1 cm, 1 dm, 1 m, . . . làm đơn vị đo diện tích thì đơn vị diện tích tương ứng là $1c{m}^2,1d{m}^2,1m^2$ . . .

2. Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông.

.

 

 

 

 

 

$S=\frac{1}{2}a.b$

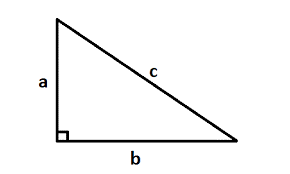3. Diện tích tam giác

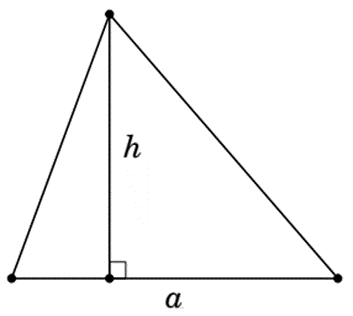
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng vớicạnh đó.

$S=\frac{1}{2}a.b$