50 Bài tập Biến đổi các biểu thức hữu tỉ – Giá trị của phân thức thường gặp (có đáp án)- Toán 8

Bài tập Toán 8 Chương 2 Bài 9: Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức

A. Bài tập Biến đổi các biểu thức hữu tỉ – Giá trị của phân thức thường gặp

I. Bài tập trắc nghiệm

Bài 1: Biến đổi biểu thức thành phân thức đại số là ?

 

 

 

Lời giải:

Ta có: 

Chọn đáp án A.

Bài 2: Biến đổi biểu thức thành phân thức đại số là ?

A. ( x – 1)²

B. – ( x – 1)²

C. ( x + 1)²

D. – ( x + 1)²

Lời giải:

Ta có:

Chọn đáp án A.

Bài 3: Với giá trị nào của x thì phân thức  xác định ?

A. x = 2.   

B. x ≠ -2.

C. x > 2.   

D. x ≤ 2.

Lời giải:

Giá trị của phân thức  xác định khi và chỉ khi 2x + 4 ≠ 0 ⇔ x ≠ – 2.

Chọn đáp án B.

Bài 4: Giá trị của biểu thức  tại x=1 là ?

A. A = 1.   

B. A = – 2.

C. A = – 1.   

D. Đáp án khác.

Lời giải:

Điều kiện xác định của phân thức là: x – 1 ≠ 0 và x + 1 ≠ 0 hay x ≠ 1 và x ≠ -1

Tại x = 1 thì phân thức đã cho không xác định nên không thể tính được giá trị của biểu thức tại x = 1 .

Chọn đáp án D.

Bài 5: Thực hiện phép tính sau , ta được kết quả là:

Lời giải:

Đáp án cần chọn là: A

Bài 6: Biết A = . Điền biểu thức thích hợp vào ô trống

Lời giải:

Ta có:

Vậy số cần điền là 1.

Đáp án cần chọn là: D

Bài 7: Trong trường hợp biểu thức A có nghĩa thì . Điều biểu thức thích hợp vào chỗ trống.

A. -x + 2         

B. x – 2          

C. -x – 2         

D. x + 2

Lời giải:

Ta có

Vậy ta cần điền là: – x – 2

Đáp án cần chọn là: C

Bài 8: Cho phân thức  Tìm điều kiện của x để phân thức xác định

A. x = 2          

B. x ≠ 2          

C. x > 2

D. x < 2

Lời giải:

Phân thức  xác định khi x – 2 ≠ 0 ⇔ x ≠ 2

Đáp án cần chọn là: B

Bài 9: Cho phân thức 

a) Tìm điều kiện của x để phân thức xác định

Lời giải:

Phân thức  xác định khi 9x² – 4 ≠ 0 ⇔ 9x² ≠ 4 ⇔ 

Đáp án cần chọn là: A

b) Tính giá trị biểu thức khi 

Lời giải:

Ta có:

  

Thay   (thỏa mãn điều kiện ) vào biểu thức   ta được: 

Vậy với x =  thì giá trị biểu thức là A = 

Đáp án cần chọn là: C

Bài 10: Cho biểu thức  Với giá trị nào của x thì B xác định

A. x ≠ {0; 2}

B. x ≠ {-2; 0; 2}

C. x ≠ {-2; 2}

D. x ≠ {0; 2}

Lời giải:

Phân thức  xác định khi

Đáp án cần chọn là: B

II. Bài tập tự luận

Bài 1. Biến đổi biểu thức sau thành một phân thức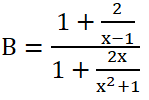 

Lời giải:

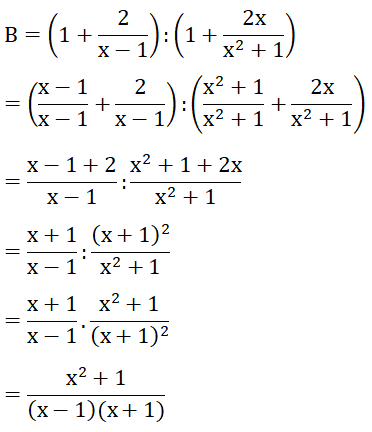
Bài 2. Cho phân thức 

a) Tìm điều kiện của x để giá trị của phân thức được xác định.

b) Tính giá trị của phân thức tại x = 1 000 000 và tại x = – 1

Lời giải:

a) Ta có: x² + x = x(x + 1)

Giá trị phân thức này được xác định với điều kiện x² + x ≠0

⇒ x(x + 1) ≠0 ⇒ x ≠0 và x + 1 ≠0

⇒ x ≠0 và x ≠-1

b) Ta có:

Vì  và x = 1 000 000 thỏa mãn điều kiện của biến nên có thể tính giá trị của phân thức đã cho bằng cách tính giá trị của phân thức rút gọn 

Vậy giá trị của phân thức đã cho tại x = 1 000 000 là 

+ Tại x= -1 phân thức đã cho không được xác định.

Vậy không tồn tại giá trị của phân thức tại x = -1

Bài 3. Biến đổi mỗi biểu thức sau thành một phân thức đại số:

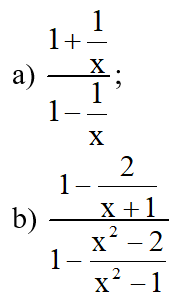
Lời giải:

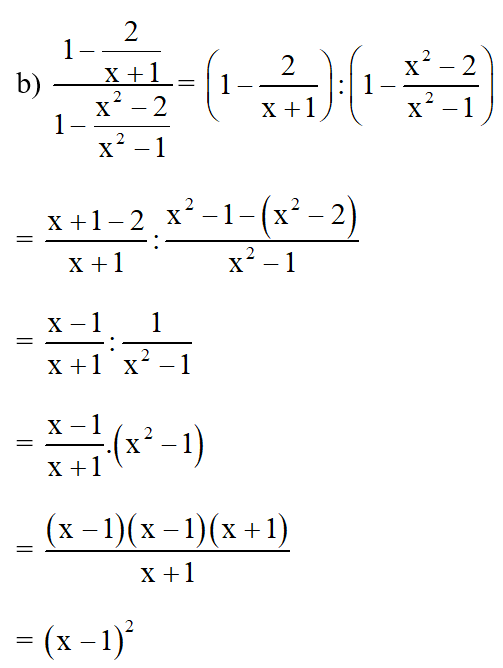
Bài 4. Với giá trị nào đó của x thì giá trị của mỗi phân thức sau được xác định?

Lời giải:

a) Giá trị của phân thức được xác định với điều kiện 2x + 4 ≠0.

Suy ra 2x ≠-4 hay x ≠-2

Vậy điều kiện để phân thức xác định là x ≠-2.

b) Điều kiện để phân thức được xác định là x2 – 1 ≠0 hay (x – 1)(x + 1) ≠0

Do đó x – 1 ≠0 và x + 1 ≠0 hay x ≠1 và x ≠-1.

Vậy điều kiện để phân thức xác định là x ≠±1.

Bài 5. Cho phân thức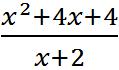 

a) Với điều kiện nào của x thì giá trị của phân thức được xác định?

b) Rút gọn phân thức.

c) Tìm giá trị của x để giá trị của phân thức bằng 1?

d) Có giá trị nào x để giá trị của phân thức bằng 0 hay không?

Lời giải:

a) Điều kiện của x để phân thức được xác định là:

x + 2 ≠0 hay x ≠-2

b) Rút gọn phân thức:

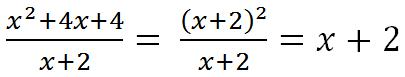
c) Nếu giá trị của phân thức đã cho bằng 1 thì x + 2 = 1.

Do đó x = -1. Giá trị này thỏa mãn điều kiện của x.

d) Nếu giá trị của phân thức đã cho bằng 0 thì x + 2 = 0 => x = -2.

Giá trị này không thỏa mãn với điều kiện của x (x ≠-2). Vậy không có giá trị nào của x để biểu thức đã cho có giá trị bằng 0.

Bài 6. Đố em tìm được phân thức (của một biến x) mà giá trị của nó được xác định với mọi giá trị của x khác các ước của 2.

Lời giải:

Các ước của 2 là ±1, ±2.

(x+ 1)(x – 1)(x + 2)(x – 2) ≠0 khi x ≠±1, x ≠±2

Vậy có thể chọn phân thức

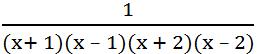
Bài 7. Thực hiện các phép tính:

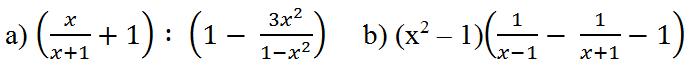
Lời giải:

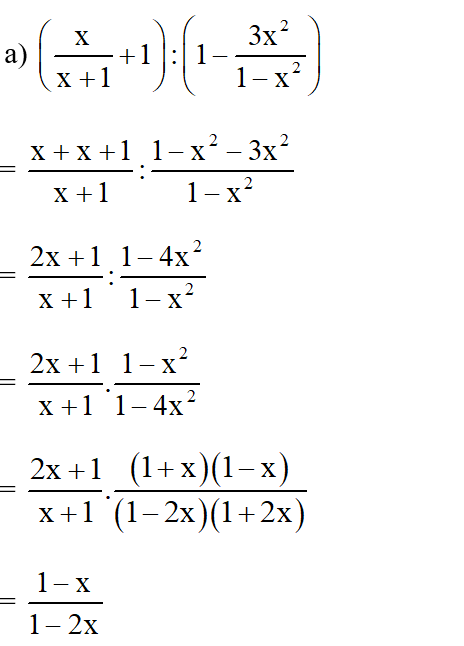
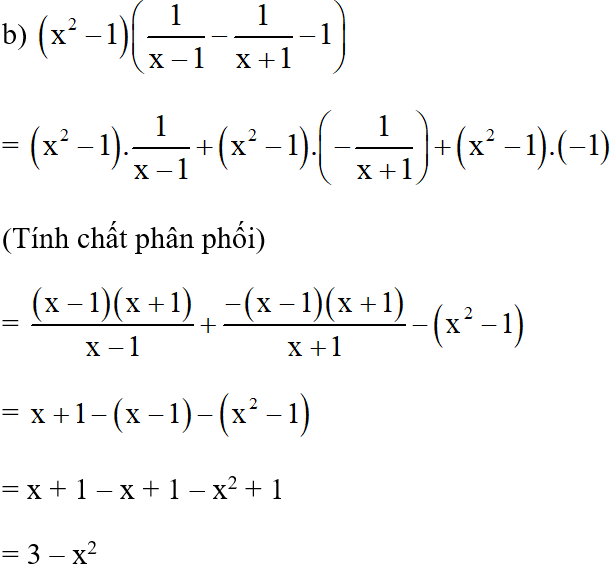
Bài 8. Làm các phép tính sau:

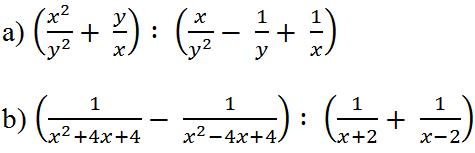
Lời giải:

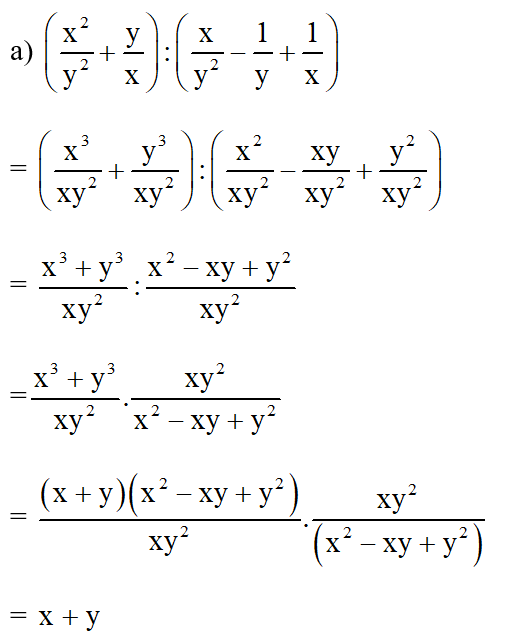
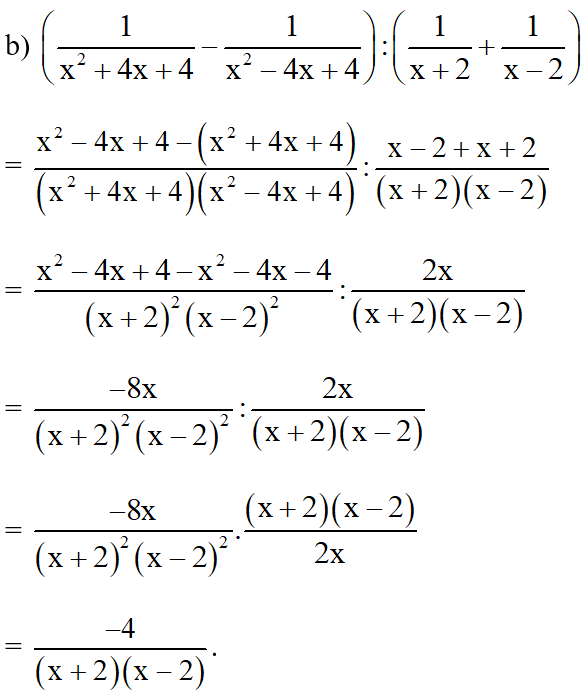
Bài 9. Chứng tỏ rằng với mọi x ≠0 và x ≠±a (a là một số nguyên), giá trị của biểu thức 

  là một số chẵn.

Lời giải:

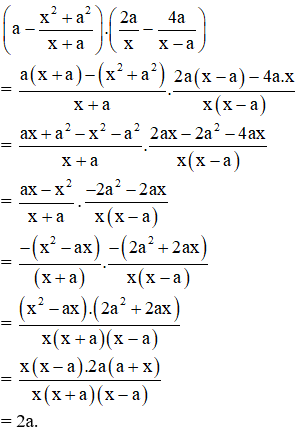
Vì a là số nguyên nên 2a là số chẵn.

Vậy giá trị của biểu thức đã cho là một số chẵn.

Bài 10. a) Biến đổi mỗi biểu thức sau thành một phân thức đại số:

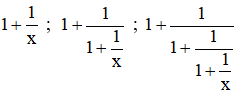
b, Em hãy dự đoán kết quả của phép biến đổi biểu thức:

thành phân thức đại số và kiểm tra lại dự đoán đó.

Lời giải:

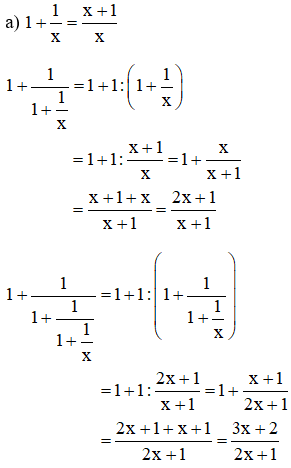
b) + Dự đoán :

Quy luật : Giả sử viết các phân thức trên thành một dãy thì phân thức sau có tử bằng tổng của tử và mẫu của phân thức đứng liền trước và mẫu bằng tử của phân thức đứng liền trước đó.

Do đó :

+ Kiểm chứng :

III. Bài tập vận dụng

Bài 1. Tìm các giá trị của x để giá trị của các phân thức được xác định:

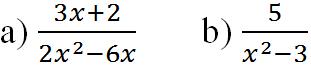
Bài 2. Biến đổi mỗi phân thức sau thành một phân thức đại số:

a) $\frac{1+\frac{1}{x}}{1-\frac{1}{x}}$

b) $\frac{1-\frac{2}{x+1}}{1-\frac{x^2-2}{x^2-1}}$

Bài 3 

a) Biến đổi mỗi biểu thức sau thành một phân thức đại số:

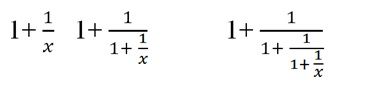
b) Em hãy dự đoán kết quả của phép biến đổi biểu thức:

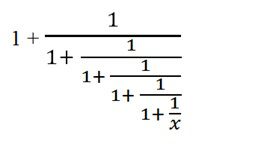
thành phân thức đại số và kiểm tra lại dự đoán đó.

Bài 4 Chứng tỏ rằng với mọi x ≠ 0 và x ≠ ±a (a là một số nguyên), giá trị của biểu thức

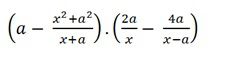
là một số chẵn.

Bài 5 Tìm các giá trị của x để giá trị của các phân thức được xác định:

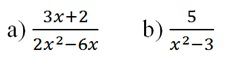
Bài 6 Cho phân thức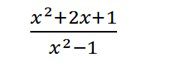

a) Với giá trị nào của x thì giá trị của phân thức được xác định ?

b) Chứng tỏ phân thức rút gọn của phân thức đã cho là

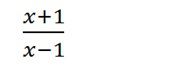
c) Để tính giá trị của phân thức đã cho tại x = 2 và x = -1, bạn Thắng đã làm như sau:

Em có đồng ý không ? Nếu không, em hãy chỉ ra chỗ mà em cho là sai.

Theo em, với những giá trị nào của biến thì có thể tính được giá trị của phân thức đã cho bằng cách tính giá trị của phân thức rút gọn ?

Bài 7 Cho phân thức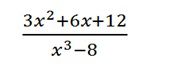

a) Với điều kiện nào của x thì giá trị của phân thức được xác định?

b) Rút gọn phân thức.

c) Em có biết trên 1 cm²bề mặt da của em có bao nhiêu con vi khuẩn không?

Tính giá trị của biểu thức đã cho tại

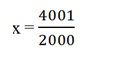
em sẽ tìm được câu trả lời thật đáng sợ. (Tuy nhiên trong số đó chỉ có 20% là vi khuẩn có hại).

Bài 8. Biến đổi biểu thức thành một phân thức

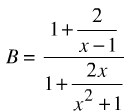
Bài 9

Đố. Đố em tìm được phân thức (của một biến x) mà giá trị của nó được xác định với mọi giá trị của x khác các ước của 2.

Bài 10. Với giá trị nào đó của x thì giá trị của mỗi phân thức sau được xác định?

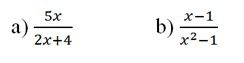
B. Lý thuyết Biến đổi các biểu thức hữu tỉ – Giá trị của phân thức thường gặp

1. Biểu thức hữu tỉ

Mỗi biểu thức là một phân thức hoặc biểu thị một dãy phép toán cộng, trừ, nhân, chia trên những phân thức gọi là biểu thức hữu tỉ.

Ví dụ. Ta có các biểu thức hữu tỉ như: $\frac{5x}{x+2};\frac{1}{x+4}-\frac{2x+2}{3x+4};$$\frac{2}{3x}+\frac{4}{x}.\frac{3}{5x+y}$; …

2. Biến đổi một biểu thức hữu tỉ thành một phân thức

Nhờ các quy tắc của các phép toán cộng, trừ, nhân, chia các phân thức, ta có thể biến đổi các biểu thức hữu tỉ thành một phân thức.

Ví dụ. Biến đổi biểu thức $\frac{1+\frac{2}{x-1}}{1+\frac{2x}{x^2+1}}$ thành một phân thức.

Hướng dẫn giải:

Ta có:

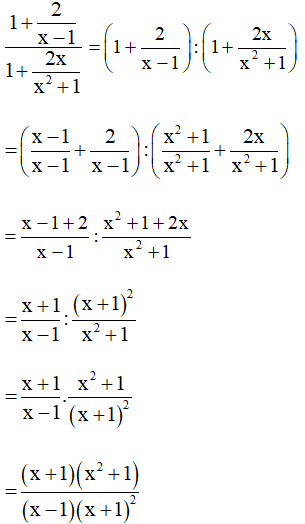
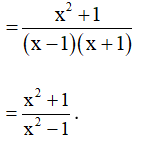
3. Giá trị của phân thức

Khi thực hiện các bài toán liên quan đến giá trị của phân thức:

+ Trước hết, phải tìm điều kiện của biến để giá trị tương ứng của mẫu thức khác 0: Điều kiện của biến để giá trị tương ứng của mẫu thức khác 0 là điều kiện để giá trị của phân thức được xác định.

+ Nếu tại giá trị của biến mà giá trị của phân thức được xác định thì phân thức ấy và phân thức được rút gọn có cùng một giá trị.

Để tính giá trị của phân thức, ta chỉ cần thay giá trị của biến vào phân thức đã được rút gọn rồi thực hiện tính như tính giá trị của biểu thức số.

Ví dụ. Cho phân thức $\frac{5x-10}{x\left(x-2\right)}$.

a) Tìm điều kiện của x để giá trị của phân thức $\frac{5x-10}{x\left(x-2\right)}$  được xác định.

b) Tính giá trị của phân thức tại x = 2020.

Hướng dẫn giải:

a) Giá trị của phân thức $\frac{5x-10}{x\left(x-2\right)}$ được xác định với điều kiện x(x – 2) ≠ 0.

Mà một tích (của nhiều số) khác 0 khi mọi thừa số đều khác 0, do đó x ≠ 0 và x – 2 ≠ 0 hay chính là x ≠ 0 và x ≠ 2.

Vậy điều kiện để giá trị của phân thức $\frac{5x-10}{x\left(x-2\right)}$ được xác định là: x ≠ 0 và x ≠ 2.

b) Ta có: $\frac{5x-10}{x\left(x-2\right)}$$=\frac{5\left(x-2\right)}{x\left(x-2\right)}=\frac{5}{x}$ và x = 2020 thỏa mãn các điều kiện của biến nên có thể tính giá trị của phân thức đã cho bằng cách tính giá trị của phân thức rút gọn $\frac{5}{x}$.

Vậy giá trị của phân thức đã cho tại x = 2020 bằng $\frac{5}{x}=\frac{5}{2020}=\frac{1}{404}$.

Xem thêm