Lý thuyết Toán 12 Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm
A. Lý thuyết Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm
1. Khoảng biến thiên
a) Định nghĩa
|
Xét mẫu số liệu ghép nhóm cho trong bảng sau, trong đó và . Gọi lần lượt là đầu mút trái của nhóm 1, đầu mút phải của nhóm m. Hiệu được gọi là khoảng biến thiên của mẫu số liệu ghép nhóm đó |

b) Ý nghĩa
- Khoảng biến thiên của mẫu số liệu ghép nhóm đo mức độ phân tán của mẫu số đó. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán
- Trong các đại lượng đo mức độ phân tán của mẫu số liệu ghép nhóm, khoảng biến thiên là đại lượng dễ hiểu, dễ tính toán. Tuy nhiên, do khoảng biến thiên chỉ sử dụng hai giá trị của mẫu số liệu nên đại lượng đó dễ bị ảnh hưởng bởi các giá trị bất thường
- Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc.
2. Khoảng tứ phân vị
a) Định nghĩa
|
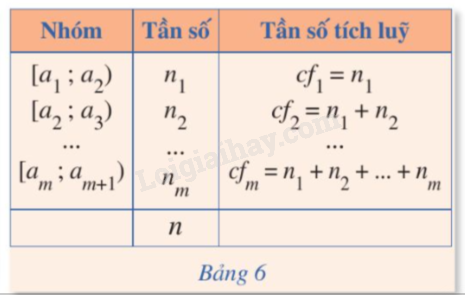
Xét mẫu số liệu ghép nhóm cho bởi bảng sau Gọi là tứ phân vị của mẫu số liệu đó. Ta gọi hiệu là khoảng tứ phân vị của mẫu số liệu đó. |
b) Ý nghĩa
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa giữa mẫu số liệu.
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm giúp xác định các giá trị bất thường của mẫu đó. Khoảng tứ phân vị thường được sử dụng thay cho khoảng biến thiên vì nó loại trừ hầu hết các giá trị bất thường của mẫu số liệu và nó không bị ảnh hưởng bởi các giá trị bất thường đó.
B. Bài tập Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm
Bài 1: Khi thống kê chiều cao (đơn vị: cm) của 120 học sinh nữ khối 10 ở một trường trung học phổ thông được kết quả từ 152 cm đến 172 cm. Nếu sử dụng mẫu số liệu ghép nhóm để biểu diễn kết quả này thì khoảng biến thiên của mẫu số liệu là:
A. 152 cm.
B. 172 cm.
C. 20 cm.
D. 10 cm.
Lời giải
Đáp án đúng là: C
Trong mẫu số liệu ghép nhóm đó, ta có: đầu mút trái của nhóm 1 là a1 = 152 cm, đầu mút phải của nhóm đó là am + 1 = 172 cm.
Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là: R = 172 – 152 = 20 cm.
Bài 2: Một mẫu số liệu ghép nhóm có tứ phân vị là Q1 = 54, Q2 = 61, Q3 = 73. Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:
A. 7.
B. 12.
C. 19.
D. 61.
Lời giải
Đáp án đúng là: C
Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó là:
∆Q = Q3 − Q1 = 73 – 54 = 19.
Bài 3: Bảng sau đây cho biết chiều cao của các học sinh lớp 12A1.
a) Tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên.
b) Lập bảng tần số tích lũy và tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.
Lời giải
a) Trong mẫu số liệu ghép nhóm trên, ta có: đầu mút trái của nhóm 1 là a1 = 145, đầu mút phải của nhóm 6 là a7 = 175.
Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:
R = a7 – a1 = 175 – 145 = 30 (cm).
b) Ta có bảng tần số tích lũy sau:
Số phần tử của mẫu là n = 43.
Ta có: mà 1 < 10,75 < 16 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy hơn hoặc bằng 10,75. Xét nhóm 3 là nhóm [155; 160) có s = 155, h = 5, n3 = 15 và nhóm 2 là nhóm [150; 155) có cf2 = 1.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
Q1 = s + = 155 + = 158,25 (cm).
Ta có: mà 28 < 32,25 < 38 nên nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn 32,25. Xét nhóm 5 là nhóm [165; 170) có t = 165, l = 5, n5 = 10 và nhóm 4 là nhóm [160; 165) có cf4 = 28.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
Q3 = t + = 165 + = 167,125 (cm).
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:
∆Q = Q3 – Q1 = 167,125 – 158,25 = 8,875 (cm).
Bài 4: Điều tra cân nặng (đơn vị: kilogram) của 50 em bé 6 tuổi, người ta được kết quả ở bảng dưới đây. Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
Lời giải
Trong mẫu số liệu ghép nhóm trên, ta có: đầu mút trái của nhóm 1 là a1 = 18, đầu mút phải của nhóm 4 là a5 = 26.
Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:
R = a5 – a1 = 26 – 18 = 8 (kg).
Bài 5: Bảng số liệu ghép nhóm dưới đây thống kê mức lương của các nhân viên của một công ty (đơn vị: triệu đồng).
Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
Lời giải
Ta có bảng tần số tích lũy của mẫu số liệu ghép nhóm trên như sau:
Số phần tử của mẫu là n = 100.
Ta có: mà 24 < 25 < 45 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 25.
Xét nhóm 2 là nhóm [30; 35) có s = 30, h = 5, n2 = 21 và nhóm 1 là nhóm [20; 30) có cf1 = 24.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
Q1 = s + = 30 + = (triệu đồng).
Ta có: mà 65 < 75 < 80 nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 75.
Xét nhóm 4 là nhóm [45; 50) có t = 45, l = 5, n4 = 15 và nhóm 3 là nhóm [40; 45) có cf3 = 65.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
Q3 = t + = 45 + = (triệu đồng).
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:
∆Q = Q3 – Q1 = − = ≈ 18,095 (triệu đồng).
Xem thêm các bài tóm tắt lý thuyết Toán lớp 12 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Lý thuyết Bài 1: Vectơ và các phép toán vectơ trong không gian
Lý thuyết Bài 2: Toạ độ của vectơ
Lý thuyết Bài 3: Biểu thức toạ độ của các phép toán vectơ
Lý thuyết Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm
Lý thuyết Bài 2: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm