Lý thuyết Toán 12 Bài 2: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm
A. Lý thuyết Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm
1. Định nghĩa
|
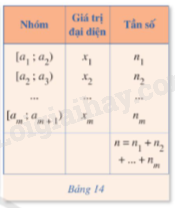
Xét mẫu số liệu ghép nhóm cho trong bảng sau:
được gọi là phương sai của mấu số liệu đó. Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là |
2. Ý nghĩa
- Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm là các xấp xỉ cho phương sai, độ lệch chuẩn của mẫu số liệu gốc, dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm đó.
- Độ lệch chuẩn có cùng đơn vị với mẫu số liệu
- Khi hai mẫu số liệu ghép nhóm có cùng đơn vị đo và có số trung bình cộng bằng nhau (hoặc xấp xỉ bằng nhau), mẫu số liệu nào có độ lệch chuẩn nhỏ hơn thì mức phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó thấp hơn
Ví dụ: Anh An đầu tư số tiền bằng nhau vào hai lĩnh vực kinh doanh A, B. Anh An thống kê số tiền thu được mỗi tháng trong vòng 60 ngày theo mỗi lĩnh vực có kết quả như sau:

So sánh giá trị trung bình và độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào mỗi lĩnh vực A, B. Đầu tư vào lĩnh vực nào “rủi ro” hơn?
Giải:
Chọn giá trị đại diện cho các nhóm số liệu ta có:

Số tiền trung bình thu được khi đầu tư vào các lĩnh vực A, B tương ứng là:
(triệu đồng)
(triệu đồng)
Như vậy, về trung bình đầu tư vào các lĩnh vực A, B số tiền thu được hàng tháng như nhau.
Độ lệch chuẩn của số tiền thu được hàng tháng khi đầu tư vào các lĩnh vực A, B tương ứng là:
Như vậy, độ lệch chuẩn của mẫu số liệu về số tiền thu được hàng tháng khi đầu tư vào lĩnh vực B cao hơn khi đầu tư vào lĩnh vực A. Người ta nói rằng, đầu tư vào lĩnh vực B là “rủi ro” hơn.
B. Bài tập Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm
Bài 1: Mẫu số liệu ghép nhóm có độ lệch chuẩn bằng 16 thì phương sai bằng:
A. 4.
B. 32.
C. 256.
D. 8.
Lời giải
Đáp án đúng là: C
Độ lệch chuẩn là căn bậc hai số học của phương sai nên phương sai bằng 162 = 256.
Bài 2: Cho bảng thống kê mẫu số liệu ghép nhóm dưới đây:
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên có kết quả gần với số nào dưới đây?
A. 11,95.
B. 10,95.
C. 13,78.
D. 120.
Lời giải
Đáp án đúng là: B
Số trung bình cộng của mẫu số liệu ghép nhóm trên là:
= = 35.
Phương sai của mẫu số liệu trên là:
s2 = .[2. (15 – 35)2 + 4. (25 – 35)2 + 8. (35 – 35)2 + 4. (45 – 35)2 + 2. (55 – 35)2]
= 120.
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là: s = ≈ 10,95.
Bài 3: Khi thống kê số khách hàng vào siêu thị trong 30 ngày đầu khai trương, người ta được kết quả là bảng tần số ghép nhóm bên dưới đây (đơn vị: người). Tính phương sai và độ lệch chuẩn của bảng thống kê đó.
Lời giải
Ta có bảng sau:
Số trung bình cộng của mẫu số liệu ghép nhóm trên là:
= = 140 (người).
Phương sai của mẫu số liệu ghép nhóm trên là:
s2 = .[3 . (90 – 140)2 + 5 . (110 – 140)2 + 6 . (130 – 140)2
+ 8 . (150 – 140)2 + 6 . (170 – 140)2 + 2 . (190 – 140)2] = ≈ 793,33.
Độ lệch chuẩn của mẫu số liệu đó là: s ≈ ≈ 28,17.
Bài 4: Một trung tâm ngoại ngữ thực hiện kiểm tra đầu vào của 80 học sinh đăng kí học, kết quả kiểm tra được cho bởi bảng tần số ghép nhóm dưới đây.
Tính phương sai và độ lệch chuẩn của mẫu số liệu trên.
Lời giải
Ta có số trung bình cộng của mẫu số liệu ghép nhóm trên là:
=
= 5,7875.
Ta có phương sai của mẫu số liệu ghép nhóm trên là:
s2 = .[2 . (0,5 – 5,7875)2 + 3 . (1,5 – 5,7875)2 + 3 . (2,5 – 5,7875)2
+ 5 . (3,5 – 5,7875)2 + 8 . (4,5 – 5,7875)2 + 20 . (5,5 – 5,7875)2
+ 16 . (6,5 – 5,7875)2 + 15 . (7,5 – 5,7875)2 + 6 . (8,5 – 5,7875)2
+ 2 . (9,5 – 5,7875)2] ≈ 3,85.
Độ lệch chuẩn của mẫu số liệu trên là: s = ≈ 1,963.
Bài 5: Tuổi thọ của một số linh kiện điện tử (đơn vị: năm) được sản xuất bởi hai phân xưởng được cho như sau:
Tính phương sai và độ lệch chuẩn của mỗi mẫu số liệu ghép nhóm trên và nhận xét về độ phân tán của tuổi thọ các linh kiện điện tử được sản xuất bởi mỗi phân xưởng.
Lời giải
Ta có bảng giá trị đại diện như sau:
Ta có n1 = 4 + 9 + 13 + 8 + 6 = 40;
n2 = 2 + 8 + 20 + 7 + 3 = 40.
Số trung bình cộng của mẫu số liệu linh kiện phân xưởng 1 là:
= = 2,7875.
Phương sai của mẫu số liệu linh kiện phân xưởng 1 là:
= .[4. (1,75 – 2,7875)2 + 9. (2,25 – 2,7875)2 + 13. (2,75 – 2,7875)2
+ 8. (3,25 – 2,7875)2 + 6. (3,75 – 2,7875)2] ≈ 0,355.
Độ lệch chuẩn của mẫu số liệu linh kiện phân xưởng 1 là: s1 ≈ ≈ 0,596.
Số trung bình cộng của mẫu số liệu linh kiện phân xưởng 2 là:
= = 2,7625.
Phương sai của mẫu số liệu linh kiện phân xưởng 2 là:
= .[2. (1,75 – 2,7625)2 + 8. (2,25 – 2,7625)2 + 20. (2,75 – 2,7625)2
+ 7. (3,25 – 2,7625)2 + 3. (3,75 – 2,7625)2] ≈ 0,219.
Độ lệch chuẩn của mẫu số liệu linh kiện phân xưởng 2 là: s2 ≈ ≈ 0,468.
Do s2 ≈ 0,468 < s1 ≈ 0,596 nên tuổi thọ linh kiện phân xưởng 2 ít phân tán hơn tuổi thọ linh kiện phân xưởng 1.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 12 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Lý thuyết Bài 1: Vectơ và các phép toán vectơ trong không gian
Lý thuyết Bài 2: Toạ độ của vectơ
Lý thuyết Bài 3: Biểu thức toạ độ của các phép toán vectơ
Lý thuyết Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm
Lý thuyết Bài 2: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm