Cho ba điểm không thẳng hàng. a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành.

Câu hỏi:

Cho ba điểm không thẳng hàng.
a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành.

Trả lời:

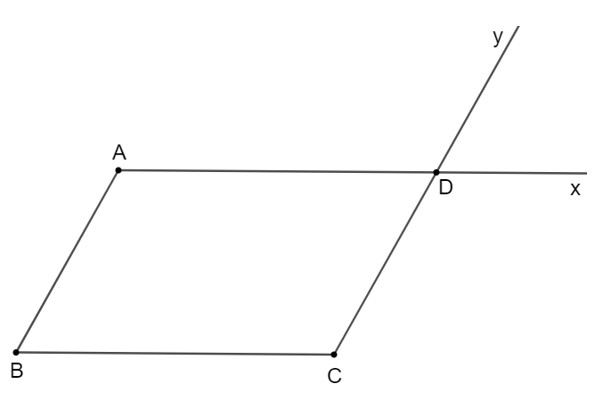
a) Gọi ba điểm không thẳng hàng đó là A, B, C.
Qua hai điểm A và C, kẻ tia Ax // BC, tia Cy // AB.
Hai tia Ax và Cy cắt nhau tại điểm D.
Khi đó điểm D là đỉnh cần tìm cùng với ba điểm đã cho để có được hình bình hành (như hình vẽ

====== **** mời các bạn xem câu tiếp bên dưới **** =====

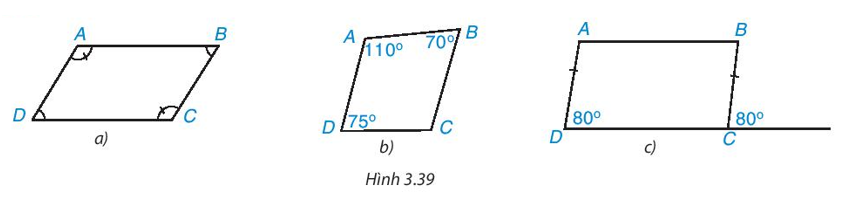
1. Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?
   
   

   Câu hỏi:
   

   Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?
   

   Trả lời:

   * Hình 3.36a)
   Tứ giác ABCD có: $\widehat{A}=\widehat{C}=100°; \widehat{B}=\widehat{D}=80°$.
   Do đó, tứ giác ABCD là hình bình hành.
   * Hình 3.36b)
   Tứ giác ABCD có: $\widehat{B}\ne \widehat{D}(70°\ne 75°)$.
   Do đó, tứ giác ABCD không là hình bình hành.
   * Hình 3.36c)
   Đặt $\widehat{BCx}=80°$ (như hình vẽ
   
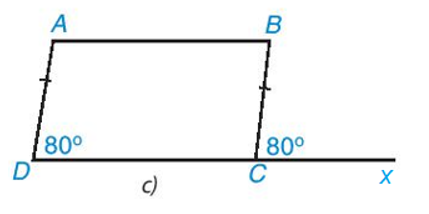
   Ta có: $\widehat{D}=\widehat{BCx}=80°$ mà hai góc này ở vị trí đồng vị nên AD // BC.
    
   Tứ giác ABCD có:
   • AD // BC (chứng minh trên)
   • AD = BC (giả thiết)
   Do đó, tứ giác ABCD là hình bình hành.
   Vậy tứ giác ABCD trong Hình 3.36a) và 3.36c) là hình bình hành; tứ giác ABCD trong Hình 3.36b) không là hình bình hành.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng: a) AN = CM;
   
   

   Câu hỏi:
   

   Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:
   a) AN = CM;

   Trả lời:

   
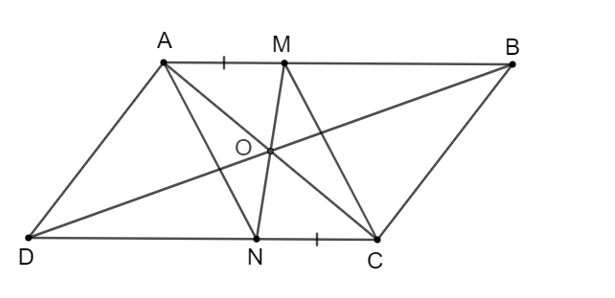
   a) Vì ABCD là hình bình hành nên AB // CD.
   Tứ giác AMCN có AM // CD (vì AB // CD); AM = CN (giả thiết).
   Suy ra, tứ giác AMCN là hình bình hành.
   Do đó AN = CM (đpcm).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. b) AMC^=ANC^
   
   

   Câu hỏi:
   

   b) $\widehat{AMC}=\widehat{ANC}$

   Trả lời:

   b) Vì tứ giác AMCN là hình bình hành suy ra $\widehat{AMC}=\widehat{ANC}$ (đpcm).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Vẽ tứ giác ABCD theo hướng dẫn sau: Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB. Bước 2. Lấy điểm C ∈ a. Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC. Hãy giải thích tại sao tứ giác ABCD là hình bình hành.
   
   

   Câu hỏi:
   

   Vẽ tứ giác ABCD theo hướng dẫn sau:
   Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB.
   Bước 2. Lấy điểm C ∈ a.
   Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC.
   Hãy giải thích tại sao tứ giác ABCD là hình bình hành.

   Trả lời:

   Ta thực hiện vẽ tứ giác ABCD theo các bước ở đề bài như sau:
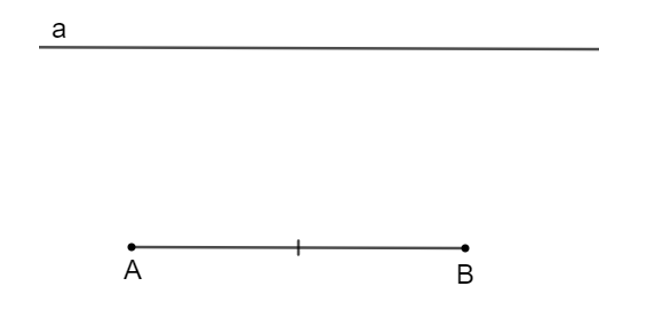
   Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB
   
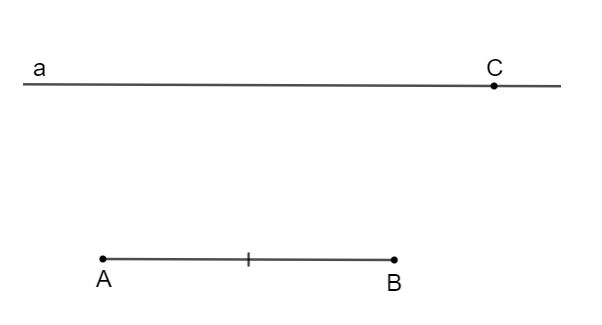
   Bước 2. Lấy điểm C ∈ a
   
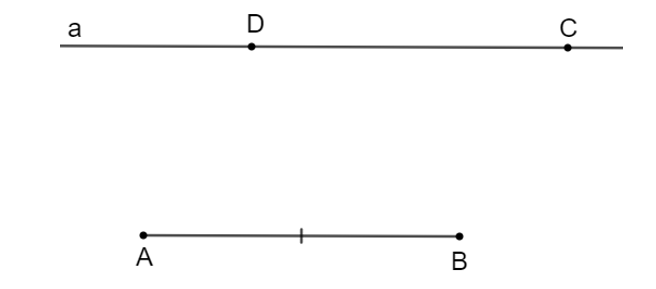
   Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC
   
   Nối AD, BC ta có tứ giác ABCD là hình bình hành
   
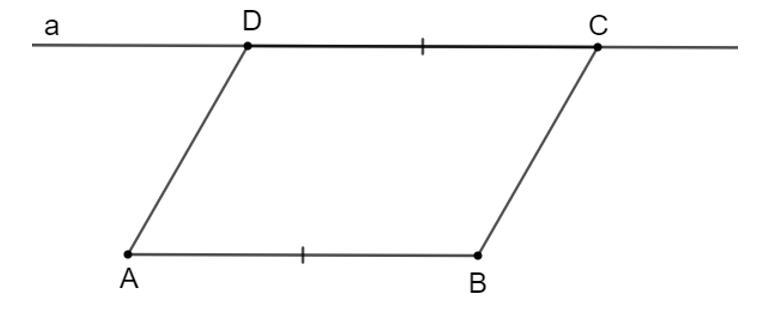
   Tứ giác ABCD là hình bình hành do:
   • AB // CD (vì AB // a; C, D ∈ a);
   • AB = CD (giả thiết).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
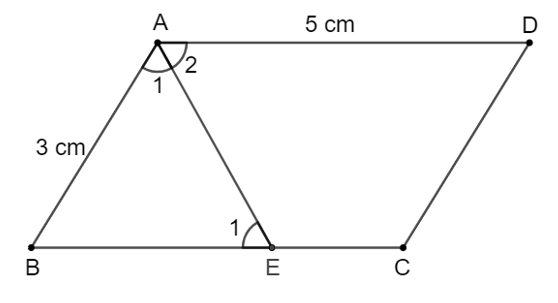
5. Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm. a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?
   
   

   Câu hỏi:
   

   Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.
   a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?

   Trả lời:

   a) Vì AD > AB (5 cm > 3 cm) nên tia phân giác của góc A cắt cạnh CD
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====