c) Qua M kẻ đường thẳng song song với BN cắt tia EN tại F. Chứng minh rằng tứ giác AFCE là hình thoi.

Câu hỏi:

c) Qua M kẻ đường thẳng song song với BN cắt tia EN tại F. Chứng minh rằng tứ giác AFCE là hình thoi.

Trả lời:

c) • Xét tứ giác BMFN có FM // BN và MB // NF (do AB // EN)
Suy ra BMFN là hình bình hành.
Do đó MB = NF.
Lại có AM = MB (do M là trung điểm AB) và AM = EN (do ANEM là hình chữ nhật)
Do đó EN = NF hay N là trung điểm của EF.
• Xét tứ giác AFCE có hai đường chéo AC và EF cắt nhau tại trung điểm của mỗi đường.
Suy ra AFCE là hình bình hành.
Lại có EF ⊥ AC nên AFCE là hình thoi.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Bạn Nam dùng 6 đoạn tre vót thẳng để làm khung diều hình thoi. Trong đó có 2 đoạn tre dài 60 cm và 80 cm để làm hai đường chéo của cái diều, 4 đoạn tre còn lại là 4 cạnh của cái diều. Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là A. 5 m. B. 1 m. C. 1,5 m. D. 2 m.
   
   

   Câu hỏi:
   

   Bạn Nam dùng 6 đoạn tre vót thẳng để làm khung diều hình thoi. Trong đó có 2 đoạn tre dài 60 cm và 80 cm để làm hai đường chéo của cái diều, 4 đoạn tre còn lại là 4 cạnh của cái diều. Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là

   A. 5 m.
   B. 1 m.
   C. 1,5 m.
   D. 2 m.

   Trả lời:

   Đáp án đúng là: D
   
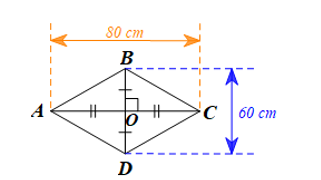
   Hình ảnh khung diều hình thoi được mô phỏng bởi hình thoi ABCD có các kích thước như hình vẽ trên.
   Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường.
   Suy ra $OB=\frac{1}{2}BD=\frac{1}{2}.60=30\left(cm\right)$ và $OA=\frac{1}{2}AC=\frac{1}{2}.80=40\left(cm\right)$.
   Áp dụng định lí Pythagore vào DOAB vuông tại O, ta có:
   AB² = OA² + OB² = 40² + 30² = 1 600 + 900 = 2 500 = 50²
   Suy ra AB = 50 cm.
   Do vậy cạnh của hình thoi có độ dài 50 cm.
   Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là:
   4.50 = 200 cm = 2 m.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình thang cân ABCD (AB // CD) có A^=65°. Số đo góc C là A. 115°. B. 95°. C. 65°. D. 125°.
   
   

   Câu hỏi:
   

   Cho hình thang cân ABCD (AB // CD) có $\widehat{A}=65°$. Số đo góc C là
   A. 115°.
   B. 95°.
   C. 65°.
   D. 125°.

   Trả lời:

   Đáp án đúng là: A
   
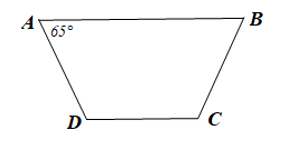
   Do ABCD là hình thang cân (AB // CD) nên $\widehat{A}+\widehat{D}=180°$
   Suy ra $\widehat{D}=180°-\widehat{A}=180°-65°=115°$.
   Mặt khác, ABCD là hình thang cân (AB // CD) nên $\widehat{C}=\widehat{D}=115°$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Trong các khẳng định sau, khẳng định nào sai? A. Tứ giác có ba góc vuông là hình chữ nhật. B. Hình bình hành có một góc vuông là hình chữ nhật. C. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình chữ nhật. D. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
   
   

   Câu hỏi:
   

   Trong các khẳng định sau, khẳng định nào sai?
   A. Tứ giác có ba góc vuông là hình chữ nhật.
   B. Hình bình hành có một góc vuông là hình chữ nhật.
   C. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.
   D. Tứ giác có các cạnh đối bằng nhau là hình bình hành.

   Trả lời:

   Đáp án đúng là: C
   Theo tính chất hình bình hành: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
   Do đó đây là tính chất đã có sẵn của hình bình hành, nên khẳng định C là sai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC vuông tại A, đường trung tuyến AM. Biết AB = 8 cm; AC = 15 cm. Độ dài đoạn AM là A. 8,5 cm. B. 8 cm. C. 7 cm. D. 7,5 cm.
   
   

   Câu hỏi:
   

   Cho tam giác ABC vuông tại A, đường trung tuyến AM. Biết AB = 8 cm; AC = 15 cm. Độ dài đoạn AM là
   A. 8,5 cm.
   B. 8 cm.
   C. 7 cm.
   D. 7,5 cm.

   Trả lời:

   Đáp án đúng là: A
   
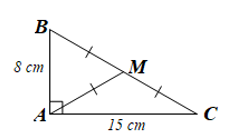
   Áp dụng định lí Pythagore vào DABC vuông tại A ta có:
   BC² = AB² + AC² = 8² + 15² = 64 + 225 = 289 = 17².
   Suy ra BC = 17 cm.
   Xét tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền BC nên bằng nửa cạnh huyền BC.
   Do đó $AM=\frac{1}{2}BC=\frac{1}{2}.17=8,5\left(cm\right)$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình thoi ABCD có cạnh bằng 13 cm, độ dài đường chéo AC là 10 cm. Độ dài đường chéo BD là A. 24 cm. B. 12 cm. C. 16 cm. D. 20 cm.
   
   

   Câu hỏi:
   

   Cho hình thoi ABCD có cạnh bằng 13 cm, độ dài đường chéo AC là 10 cm. Độ dài đường chéo BD là
   A. 24 cm.
   B. 12 cm.
   C. 16 cm.
   D. 20 cm.

   Trả lời:

   Đáp án đúng là: A
   
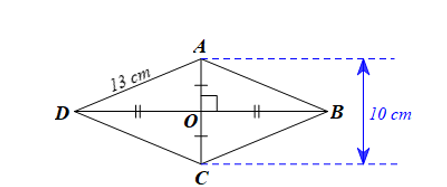
   Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường.
   Suy ra $OD=\frac{1}{2}BD$ và $OA=\frac{1}{2}AC=\frac{1}{2}.10=5\left(cm\right)$.
   Áp dụng định lí Pythagore vào DOAD vuông tại O, ta có:
   AD² = OA² + OD²
   Suy ra $OD=\sqrt{A{D}^2-O{A}^2}=\sqrt{{13}^2-5^2}=12\left(cm\right)$.
   Do đó BD = 2OD = 2.12 = 24 (cm).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====