Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ tiếp tuyến AB và cát tuyến ACD. Vẽ dây BM vuông góc với tia phân giác của góc BAC, dây này cắt CD tại E. Chứng minh rằng:a) BM là tia phân giác của góc CBDb) MD2 = ME.MB

Câu hỏi:

Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ tiếp tuyến AB và cát tuyến ACD. Vẽ dây BM vuông góc với tia phân giác của góc BAC, dây này cắt CD tại E. Chứng minh rằng:a) BM là tia phân giác của góc CBDb) ${\mathrm{MD}}^2$ = ME.MB

Trả lời:

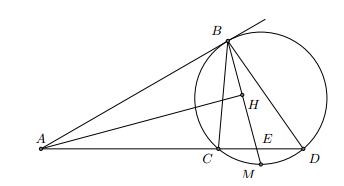
====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Một đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của các cung AB và AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh  là tam giác cân.
   
   

   Câu hỏi:
   

   Một đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của các cung AB và AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh  là tam giác cân.

   Trả lời:

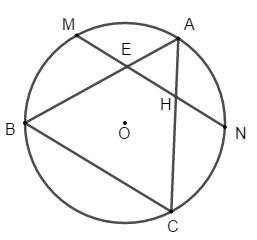   Ta có

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình thang ABCD có AB // CD và AD = DC = CB nội tiếp trong đường tròn đường kính AB. Tính số đo của góc AIB^ với I là giao điểm của AC và BD.
   
   

   Câu hỏi:
   

   Cho hình thang ABCD có AB // CD và AD = DC = CB nội tiếp trong đường tròn đường kính AB. Tính số đo của góc $\widehat{\mathrm{AIB}}$ với I là giao điểm của AC và BD.

   Trả lời:

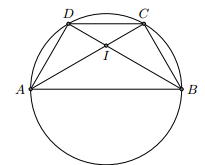   Từ giả thiết, ta nhận được:

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Từ một điểm M ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến MB, MC. Vẽ đường kính BOD. Hai đường thẳng CD và MB cắt nhau tại A. Chứng minh rằng M là trung điểm của AB.
   
   

   Câu hỏi:
   

   Từ một điểm M ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến MB, MC. Vẽ đường kính BOD. Hai đường thẳng CD và MB cắt nhau tại A. Chứng minh rằng M là trung điểm của AB.

   Trả lời:

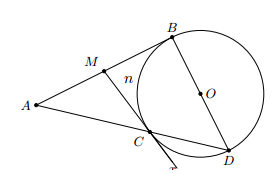   Vì tính chất của hai tiếp tuyến nên MB = MC (1)Từ (1) và (2) suy ra MA = MB, tức M là trung điểm AB.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
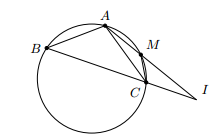
4. Cho đường tròn (O) và hai dây cung bằng nhau AB, AC. Trên cung nhỏ AC lấy điểm M. Gọi I là giao điểm của AM và BC. Chứng minh rằng AIC^=ACM^
   
   

   Câu hỏi:
   

   Cho đường tròn (O) và hai dây cung bằng nhau AB, AC. Trên cung nhỏ AC lấy điểm M. Gọi I là giao điểm của AM và BC. Chứng minh rằng $\widehat{\mathrm{AIC}}=\widehat{\mathrm{ACM}}$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
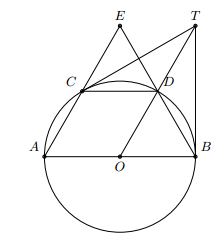
5. Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho sdAC⏜=sdCD⏜=sdDB⏜=600. Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:a) AEB^=BTC^b) CD là tia phân giác của BCT^
   
   

   Câu hỏi:
   

   Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho $\mathrm{sd}\stackrel{⏜}{\mathrm{AC}}=\mathrm{sd}\stackrel{⏜}{\mathrm{CD}}=\mathrm{sd}\stackrel{⏜}{\mathrm{DB}}={60}^0$. Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:a) $\widehat{\mathrm{AEB}}=\widehat{\mathrm{BTC}}$b) CD là tia phân giác của $\widehat{\mathrm{BCT}}$

   Trả lời:

   a) Ta có:Vậy ta được CD là tia phân giác của góc BCT.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====