Cho ∆ABC nhọn và AB < AC nội tiếp đường tròn tâm O. Gọi D, E, F lần lượt là điểm chính giữa của các cung nhỏ AB, BC, CA. Tiếp tuyến tại A của đường tròn cắt các đường thẳng BC và DF lần lượt tại M và N. Gọi P và Q lần lượt là giao điểm của đường thẳng BC với đường thẳng DF và AE.a) Chứng minh rằng AE⊥DFb) Chứng minh rằng MA = MQ, MN = MP

Câu hỏi:

Cho $∆\mathrm{ABC}$ nhọn và AB < AC nội tiếp đường tròn tâm O. Gọi D, E, F lần lượt là điểm chính giữa của các cung nhỏ AB, BC, CA. Tiếp tuyến tại A của đường tròn cắt các đường thẳng BC và DF lần lượt tại M và N. Gọi P và Q lần lượt là giao điểm của đường thẳng BC với đường thẳng DF và AE.a) Chứng minh rằng $\mathrm{AE}\perp \mathrm{DF}$b) Chứng minh rằng MA = MQ, MN = MP

Trả lời:

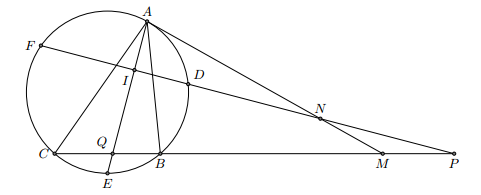Trước hết, từ giả thiết “D, E, F lần lượt là điểm chính giữa của các cung nhỏ AB, BC, CA” ta được:a) Gọi I là giao điểm của AE và DF, ta có ngay:b) Xét $∆\mathrm{MAQ}$ sử dụng định lí về góc tạo bởi tia tiếp tuyến với một dây và góc có đỉnh ở bên trong đường tròn ta cóXét $∆\mathrm{MNP}$, sử dụng định lí về góc có đỉnh ở bên ngoài đường tròn và hai góc đối đỉnh. Ta có:

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Một đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của các cung AB và AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh  là tam giác cân.
   
   

   Câu hỏi:
   

   Một đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của các cung AB và AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh  là tam giác cân.

   Trả lời:

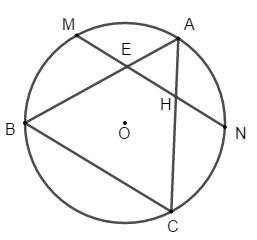   Ta có

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình thang ABCD có AB // CD và AD = DC = CB nội tiếp trong đường tròn đường kính AB. Tính số đo của góc AIB^ với I là giao điểm của AC và BD.
   
   

   Câu hỏi:
   

   Cho hình thang ABCD có AB // CD và AD = DC = CB nội tiếp trong đường tròn đường kính AB. Tính số đo của góc $\widehat{\mathrm{AIB}}$ với I là giao điểm của AC và BD.

   Trả lời:

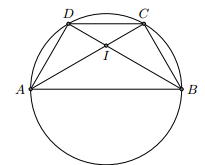   Từ giả thiết, ta nhận được:

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Từ một điểm M ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến MB, MC. Vẽ đường kính BOD. Hai đường thẳng CD và MB cắt nhau tại A. Chứng minh rằng M là trung điểm của AB.
   
   

   Câu hỏi:
   

   Từ một điểm M ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến MB, MC. Vẽ đường kính BOD. Hai đường thẳng CD và MB cắt nhau tại A. Chứng minh rằng M là trung điểm của AB.

   Trả lời:

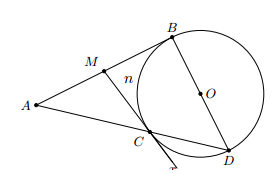   Vì tính chất của hai tiếp tuyến nên MB = MC (1)Từ (1) và (2) suy ra MA = MB, tức M là trung điểm AB.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho đường tròn (O) và hai dây cung bằng nhau AB, AC. Trên cung nhỏ AC lấy điểm M. Gọi I là giao điểm của AM và BC. Chứng minh rằng AIC^=ACM^
   
   

   Câu hỏi:
   

   Cho đường tròn (O) và hai dây cung bằng nhau AB, AC. Trên cung nhỏ AC lấy điểm M. Gọi I là giao điểm của AM và BC. Chứng minh rằng $\widehat{\mathrm{AIC}}=\widehat{\mathrm{ACM}}$

   Trả lời:

   

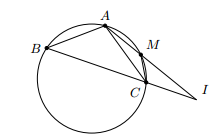
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho sdAC⏜=sdCD⏜=sdDB⏜=600. Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:a) AEB^=BTC^b) CD là tia phân giác của BCT^
   
   

   Câu hỏi:
   

   Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho $\mathrm{sd}\stackrel{⏜}{\mathrm{AC}}=\mathrm{sd}\stackrel{⏜}{\mathrm{CD}}=\mathrm{sd}\stackrel{⏜}{\mathrm{DB}}={60}^0$. Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:a) $\widehat{\mathrm{AEB}}=\widehat{\mathrm{BTC}}$b) CD là tia phân giác của $\widehat{\mathrm{BCT}}$

   Trả lời:

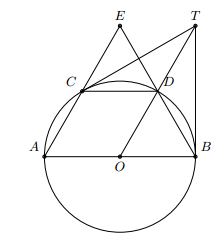   a) Ta có:Vậy ta được CD là tia phân giác của góc BCT.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====