Câu hỏi:
Cho đường tròn tâm O.Gọi I là điểm chính giữa của cung AB (không phải là cung nửa đường tròn) và H là trung điểm của dây AB .Chứng minh rằng đường thẳng IH đi qua tâm O của đường tròn
Trả lời:
Suy ra : IA =IB (hai cung bằng nhau căng hai dây bằng nhau)Hay I nằm trên đường trung trực của ABMà OA =OB (=R)Nên O nằm trên đường trung trực của ABSuy ra OI là đường trung trực của ABVì H là trung điểm của AB nên OI đi qua trung điểm HVậy ba điểm I, H, O thẳng hàng
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có AB > AC .Trên cạnh AB lấy điểm D sao cho AD = AC đường tròn tâm O ngoại tiếp tam giác BCD .Từ O lần lượt hạ các đường vuông góc OH,OK xuống BC và BD (H ∈ BC , K ∈ BD). Chứng minh rằng OH < OK
Câu hỏi:
Cho tam giác ABC có AB > AC .Trên cạnh AB lấy điểm D sao cho AD = AC đường tròn tâm O ngoại tiếp tam giác BCD .Từ O lần lượt hạ các đường vuông góc OH,OK xuống BC và BD (H ∈ BC , K ∈ BD). Chứng minh rằng OH < OK
Trả lời:
Áp dụng bất đẳng thức tam giác vào ΔABC , ta có: BC > AB – AC mà AC = AD (gt)suy ra : BC > AB – AD hay : BC > BDVì trong một đường tròn ,dây cung lớn hơn gần tâm hơn nên: OH < OK
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có AB > AC .Trên cạnh AB lấy điểm D sao cho AD = AC đường tròn tâm O ngoại tiếp tam giác BCD .Từ O lần lượt hạ các đường vuông góc OH,OK xuống BC và BD (H ∈ BC , K ∈ BD). So sánh hai cung nhỏ BD và BC
Câu hỏi:
Cho tam giác ABC có AB > AC .Trên cạnh AB lấy điểm D sao cho AD = AC đường tròn tâm O ngoại tiếp tam giác BCD .Từ O lần lượt hạ các đường vuông góc OH,OK xuống BC và BD (H ∈ BC , K ∈ BD). So sánh hai cung nhỏ BD và BC
Trả lời:
Theo câu a ,BC > BDVì trong một đường tròn, dây cung lớn hơn căng cung lớn hơn nên :
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trên dây cung AB của một đường tròn O,lấy hai điểm C và D chia dây này thành 3 đoạn thẳng bằng nhau AC = CD =DB.Các bán kính qua C và D cắt cung nhỏ AB lần lượt tại E và FChứng minh rằng : ∠AE = ∠FB
Câu hỏi:
Trên dây cung AB của một đường tròn O,lấy hai điểm C và D chia dây này thành 3 đoạn thẳng bằng nhau AC = CD =DB.Các bán kính qua C và D cắt cung nhỏ AB lần lượt tại E và FChứng minh rằng : AE = FB
Trả lời:

====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trên dây cung AB của một đường tròn O,lấy hai điểm C và D chia dây này thành 3 đoạn thẳng bằng nhau AC = CD =DB.Các bán kính qua C và D cắt cung nhỏ AB lần lượt tại E và FChứng minh rằng : ∠AE = ∠EF
Câu hỏi:
Trên dây cung AB của một đường tròn O,lấy hai điểm C và D chia dây này thành 3 đoạn thẳng bằng nhau AC = CD =DB.Các bán kính qua C và D cắt cung nhỏ AB lần lượt tại E và FChứng minh rằng : AE = EF
Trả lời:
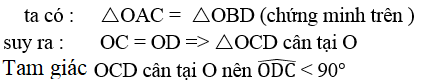
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đường tròn tâm O.Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB,nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng: Hai cung nhỏ CF và BD bằng nhau
Câu hỏi:
Cho đường tròn tâm O.Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB,nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng: Hai cung nhỏ CF và BD bằng nhau
Trả lời:
Ta có : ABF nội tiếp trong (O) và AB là đường kính cuả (O) nên ΔABF vuông tại FSuy ra: BF ⊥ AKMà AK ⊥ CD (gt)Nên : BF // CDSuy ra: BD = CF(hai cung bị chắn giữa hai dây song song thì bằng nhau)
====== **** mời các bạn xem câu tiếp bên dưới **** =====