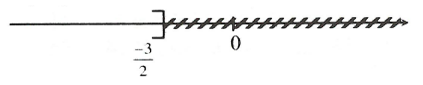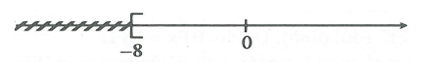Bộ 21 Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2022 – 2023 – Đề 1
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề 1)
Câu 1. (1,5 điểm) Cho biểu thức : A = \(\frac{{3x + 15}}{{{x^2} – 9}} + \frac{1}{{x + 3}} – \frac{2}{{x – 3}}\) ( với x \( \ne \pm \) 3 )
a, Rút gọn biểu thức A
b, Tìm x để A = \(\frac{1}{2}\)
Câu 2. (2,0 điểm) Giải các phương trình và bất phương trình sau:
a, \(\left| {x + 5} \right| = 3x + 1\)
b, \(\frac{{3\left( {x – 1} \right)}}{4} + 1 \ge \frac{{x + 2}}{3}\)
c, \[\frac{{x – 2}}{{x + 2}} – \frac{3}{{x – 2}} = \frac{{2(x – 11)}}{{{x^2} – 4}}\]
Câu 3. (2,0 điểm) Giải bài toán sau bằng cách lập phương trình:
Một người đi ô tô từ A đến B với vận tốc 35 km/h. Lúc từ B về A người đó đi với vận tốc bằng \(\frac{6}{5}\) vận tốc lúc đi . Do đó thời gian về ít hơn thời gian đi là 30 phút. Tính quãng đường AB.
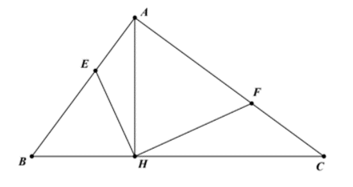
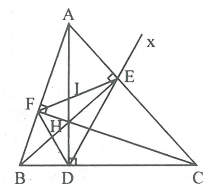
Câu 4. (4,0 điểm) Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H
a) Chứng minh \[\Delta AEB\] đđồng dạng với \[\Delta AFC\]. Từ đó suy ra AF.AB = AE. AC
b) Chứng minh: \[\widehat {AEF} = \widehat {ABC}\]
c) Cho AE = 3cm, AB= 6cm. Chứng minh rằng SABC = 4SAEF
Câu 5. (0,5 điểm) Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 12 cm, AD = 16 cm, AA’ = 25 cm. Tính diện tích toàn phần và thể tích hình hộp chữ nhật.
Câu 6. (0,5 điểm) Cho 3 số a,b,c thỏa mãn a + b + c = 2. tìm giá trị nhỏ nhất của biểu thức: A = a\(^2\)+ b\(^2\)+ c\(^2\)
Đáp án
|
———-HẾT———Câu |
Đáp án và hướng dẫn chấm |
Biểu điểm |
|
Câu 1 (2,0 điểm) |
A = \(\frac{{3x + 15}}{{{x^2} – 9}} + \frac{1}{{x + 3}} – \frac{2}{{x – 3}}\) ( x\( \ne \pm \) 3 ) = \(\frac{{3x + 15}}{{\left( {x + 3} \right)\left( {x – 3} \right)}}\)+ \(\frac{1}{{x + 3}}\)- \(\frac{2}{{x – 3}}\) = \(\frac{{3x + 15 + x – 3 – 2x – 6}}{{\left( {x + 3} \right)\left( {x – 3} \right)}}\) = \(\frac{{2x + 6}}{{\left( {x + 3} \right)\left( {x – 3} \right)}}\) =\(\frac{2}{{x – 3}}\) |
0,5 điểm
0,5 điểm |
|
b) ĐK : \(x \ne \pm 3\) Xét: \(A = \frac{1}{2} \Rightarrow \frac{2}{{x – 3}} = \frac{1}{2} \Leftrightarrow x – 3 = 4 \Leftrightarrow x = 7\)(thỏa mãn điều kiện) Vậy x = 7 thì A =\(\frac{1}{2}\). |
0,5 điểm
0,5 điểm |
|
|
Câu 2 (2,5 điểm) |
Xét phương trình: \(\left| {x + 5} \right| = 3x + 1\) TH1: x+5 = 3x+1 với x\( \ge – 5\) x = 2 (nhận) TH2: –x -5 =3x+1 với x < -5 x = \(\frac{{ – 3}}{2}\) (loại ) Vậy nghiệm của phương trình là x = 2. |
0,25 điểm
0,25 điểm
0,25 điểm |
|
b) Xét bất phương trình: \[\frac{{x + 6}}{5} – \frac{{x – 2}}{3} < 2\]\(\) \(\begin{array}{l} \Leftrightarrow \frac{{3(x + 6) – 5(x – 2)}}{{15}} < \frac{{30}}{{15}}\\ \Leftrightarrow 3x + 18 – 5x + 10 < 30\\ \Leftrightarrow – 2x < 2\\ \Leftrightarrow x > – 1\end{array}\) Vậy tập nghiệm của BPT là: \(S = \left\{ {\left. x \right|x > – 1} \right\}\). |
0,25 điểm
0,25 điểm
0,25 điểm |
|
|
c) \[\frac{{x – 2}}{{x + 2}} – \frac{3}{{x – 2}} = \frac{{2(x – 11)}}{{{x^2} – 4}}\] ĐKXĐ: \[x \ne \pm 2\] \[\frac{{x – 2}}{{x + 2}} – \frac{3}{{x – 2}} = \frac{{2(x – 11)}}{{{x^2} – 4}}\] \( \Rightarrow \left( {x – 2} \right)\left( {x – 2} \right) – 3\left( {x + 2} \right) = 2\left( {x – 11} \right)\) \[\begin{array}{l} \Leftrightarrow {x^2} – 4x + 4 – 3x – 6 – 2x + 22 = 0\\ \Leftrightarrow {x^2} – 9x + 20 = 0\\ \Leftrightarrow {x^2} – 4x – 5x + 20 = 0\\ \Leftrightarrow x(x – 4) – 5(x – 4) = 0\\ \Leftrightarrow (x – 4)(x – 5) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x – 4 = 0\\x – 5 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 4(TM)\\x = 5(TM)\end{array} \right.\end{array}\] Vậy tập nghiệm của phương trình là: S={4;5}. |
0,25 điểm
0,5 điểm
0,25 điểm |
|
|
Câu 3 (1,5 điểm) |
Gọi quãng đường AB là x(km) (x > 0 ) Vận tốc từ B dến A : 42 km/h Thời gian từ A đến B là : \[\frac{x}{{35}}\] (h) Thời gian từ B đến A là : \[\frac{x}{{42}}\] (h) Theo đề bài ta có phương trình :\[\frac{x}{{35}} – \frac{x}{{42}} = \frac{1}{2}\] Giải phương trình được: x = 105 (t/m) Quãng đường AB là 105 km. |
0,25 điểm
0,25 điểm
0,25 điểm
0,5 điểm
0,25 điểm |
|
Câu 4 (2,5 điểm) |
– Vẽ hình đúng
Xét tam giác AEB và tam giác AFC có: \[\begin{array}{l}\widehat {AEB} = \widehat {AFC} = {90^0}\\\widehat A\,\,\,chung\end{array}\] Do đó: \[\Delta AEB \sim \Delta AFC\left( {g.g} \right)\] Suy ra: \[\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}\,\,\,\,\,\,hay\,\,\,\,AF.AB = AE.AC\] |
0,5 điểm
0,5 điểm 0,25 điểm
|
|
b. Xét tam giác AEF và tam giác ABC có: Â chung \[\frac{{AF}}{{AC}} = \frac{{AE}}{{AB}}\]( chứng minh trên) Do đó: \[\Delta AEF \sim \Delta ABC\left( {c.g.c} \right)\] |
0,5 điểm
0,25 điểm |
|
|
c. Ta có : \[\Delta AEF \sim \Delta ABC\](cmt) suy ra : \[\frac{{{S_{AEF}}}}{{{S_{ABC}}}} = {\left( {\frac{{AE}}{{AB}}} \right)^2} = {\left( {\frac{3}{6}} \right)^2} = \frac{1}{4}\] hay SABC = 4SAEF |
0,25 điểm
0,25 điểm |
|
|
Câu 5 (0,5 điểm) |
Diện tích toàn phần của hình hộp chữ nhật: \({S_{tp}} = {S_{xq}} + 2{S_d}\) = 2p.h + 2 S = 2 (AB + AD).AA’ + 2 AB.AD = 2 (12 + 16).25 + 2.12.16 = 1400 + 384 = 1784 ( cm2 ) Thể tích hình hộp chữ nhật V= S.h = AB.AD.AA’ = 12.16.25 = 4800 ( cm3 ). |
0,25 điểm
0,25 điểm |
|
Câu 6 (1,0 điểm) |
Chỉ ra được 4 = a\(^2\)+ b\(^2\)+ c\(^2\)+ 2(ab + bc + ca ) Mà a\(^2\)+ b\(^2\)+ c\(^2\)\( \ge \) ab + bc + ca Suy ra 4 \( \le \) 3 ( a\(^2\)+ b\(^2\)+ c\(^2\)) \( \Rightarrow \) a\(^2\)+ b\(^2\)+ c\(^2\)\( \ge \) \(\frac{4}{3}\)\( \Rightarrow \) Min A = \(\frac{4}{3}\), đạt được khi a = b = c = \(\frac{2}{3}\) |
0,25 điểm
0,5 điểm
0,25 điểm |
Chú ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa
Bộ 21 Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2022 – 2023 – Đề 2
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề 2)
Câu 1. (2 điểm) Cho biểu thức:
\({\rm{P}} = \left( {\frac{3}{{2x + 4}} + \frac{x}{{2 – x}} + \frac{{2{x^2} + 3}}{{{x^2} – 4}}} \right):\frac{{2x – 1}}{{4x – 8}}{\rm{ }}\)với \(x \ne \pm 2;{\rm{ }}x \ne \frac{1}{2}\).
a) Chứng minh \(P = \frac{{2x}}{{x + 2}}\)
b) Tính giá trị của P khi biết \(4{x^2} – 1 = 0\).
c) Tim \(x\) để \(P < 2\).
Câu 2. (2,0 điểm) Giải bài toán sau bằng cách lập phương trình:
Một người đi từ \(A\) đến \(B\) với vận tốc \(36\;{\rm{km}}/{\rm{h}}\). Khi đến B, người đó nghỉ lại 30 phút rồi quay trở về A với vận tốc lớn hơn vận tốc lúc đi là \(9\;{\rm{km}}/{\rm{h}}\). Thời gian kể từ lúc đi từ \(A\) đến lúc trở về đến A là 5 giờ. Tính quãng đường \({\rm{AB}}\).
Câu 3. (2,0 điểm) Giải các phương trình và các bất phương trình sau:
a) \({(2x – 1)^2} – x(x – 3) = 1\)
b) \(\frac{1}{{x + 2}} + \frac{3}{{3 – x}} = \frac{{5x}}{{{x^2} – x – 6}}\)
c) \(\frac{{x + 3}}{5} – \frac{{3 – x}}{3} > \frac{{2x – 3}}{2}\)
Câu 4. (3,5 điểm) Cho tam giác ABC vuông tại \(A\), đường cao AH
a) Chứng minh \(\Delta ABH\) đồng dạng với \(\Delta CAH\), tù đó suy ra \({\rm{A}}{{\rm{H}}^2} = {\rm{BH}}\). CH.
b) Cho \({\rm{BH}} = 4\;{\rm{cm}},{\rm{BC}} = 13\;{\rm{cm}}.\) Tính \({\rm{AH}},{\rm{AB}}\).
c) Gọi E là điểm tùy ý trên cạnh AB, đường thẳng qua \({\rm{H}}\) và vuông góc với \({\rm{HE}}\) cắt cạnh \({\rm{AC}}\) tại \(F\). Chứng minh: \({\rm{AE}}\). \({\rm{CH}} = {\rm{AH}}\). FC.
d) Tìm vị trí của điểm \({\rm{E}}\) trên cạnh \({\rm{AB}}\) đề tam giác EHF có diện tích nhỏ nhất.
Câu 5. (0,5 điểm) Cho ba số dương x, y, z thỏa mãn điều kiện \(x + y + z = 4\).
Tìm giá trị nhỏ nhất của \({\rm{A}} = \frac{4}{{x + 1}} + \frac{9}{{y + 2}} + \frac{{25}}{{z + 3}}\).
———-HẾT———
Đáp án
|
Câu |
Đáp án và hướng dẫn chấm |
Biểu điểm |
|
Câu 1 (2,0 điểm) |
a) Xét biểu thức: \({\rm{P}} = \left( {\frac{3}{{2x + 4}} + \frac{x}{{2 – x}} + \frac{{2{x^2} + 3}}{{{x^2} – 4}}} \right):\frac{{2x – 1}}{{4x – 8}}{\rm{ }}\)với \(x \ne \pm 2;{\rm{ }}x \ne \frac{1}{2}\). \(\begin{array}{l}{\rm{P}} = \left( {\frac{{3\left( {x – 2} \right)}}{{2\left( {x + 2} \right)\left( {x – 2} \right)}} – \frac{{2x\left( {x + 2} \right)}}{{2\left( {x – 2} \right)\left( {x + 2} \right)}} + \frac{{2\left( {2{x^2} + 3} \right)}}{{2\left( {x – 2} \right)\left( {x + 2} \right)}}} \right):\frac{{2x – 1}}{{4x – 8}}\\{\rm{P}} = \left( {\frac{{3x – 6 – 2{x^2} – 4x + 4{x^2} + 6}}{{2\left( {x + 2} \right)\left( {x – 2} \right)}}} \right):\frac{{2x – 1}}{{4x – 8}}\\{\rm{P}} = \left( {\frac{{2{x^2} – x}}{{2\left( {x + 2} \right)\left( {x – 2} \right)}}} \right):\frac{{2x – 1}}{{4x – 8}}\end{array}\) \(P = \frac{{x(2x – 1)}}{{2(x – 2)(x + 2)}} \cdot \frac{{4(x – 2)}}{{2x – 1}}\) \(P = \frac{{2x}}{{x + 2}}\) Vậy \(P = \frac{{2x}}{{x + 2}}\). |
0,5 điểm
0,25 điểm |
|
b) Ta xét phương trình \(4{x^2} – 1 = 0\) \(\begin{array}{l} \Leftrightarrow 4{x^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{2}(KTM)\\x = – \frac{1}{2}(TM)\end{array} \right.\end{array}\) Thay \(x = – \frac{1}{2}\) vào biểu thức P, ta được: \(P = \frac{{2\left( { – \frac{1}{2}} \right)}}{{ – \frac{1}{2} + 2}} = \frac{{ – 1}}{{\frac{3}{2}}} = – \frac{2}{3}\) Vậy \(P = – \frac{2}{3}\). |
0,25 điểm
0,25 điểm |
|
|
c) Xét P < 2 \(\begin{array}{l} \Leftrightarrow \frac{{2x}}{{x + 2}} < 2\\ \Leftrightarrow \frac{{2x}}{{x + 2}} – 2 < 0\\ \Leftrightarrow \frac{{2x}}{{x + 2}} – \frac{{2\left( {x + 2} \right)}}{{x + 2}} < 0\\ \Leftrightarrow \frac{{ – 4}}{{x + 2}} < 0\end{array}\) Vì \( – 4 < 0\) nên \(\frac{{ – 4}}{{x + 2}} < 0 \Leftrightarrow x + 2 > 0 \Leftrightarrow x > – 2\) Vậy với \(x > – 2,x \ne 2,x \ne \frac{1}{2}\) thì P < 2. |
0,25 điểm
0,25 điểm |
|
|
Câu 2 (1,5 điểm) |
Gọi độ dài quãng đường \({\rm{AB}}\) là \({\rm{x}}({\rm{km}}){\rm{ }}({\rm{x}} > 0)\) Thời gian người đó đi từ \({\rm{A}}\) đến \({\rm{B}}\) là: \(\frac{x}{{36}}\)(h) Vận tốc khi người đó đi từ \({\rm{B}}\) về \({\rm{A}}\) là: \(36 + 9 = 45(\;{\rm{km}})\) Thời gian người đó đi từ \({\rm{B}}\) về \({\rm{A}}\) là: \(\frac{x}{{45}}\)(h) Lập luận đến phương trình \(\frac{x}{{36}} + \frac{x}{{45}} = \frac{9}{2}\) Giải phương trình được \({\rm{x}} = 90\) Vậy độ dài quãng đường AB là 90 km. |
0,25 điểm
0,5 điểm
0,5 điểm)
0,25 điểm |
|
Câu 3 (2,5 điểm) |
a) Xét phương trình: \({(2x – 1)^2} – x(x – 3) = 1\) \( \Leftrightarrow 4{x^2} – 4x + 1 – {x^2} + 3x = 1\) \(\begin{array}{l} \Leftrightarrow 3{x^2} – x = 0\\ \Leftrightarrow x\left( {3x – 1} \right) = 0\end{array}\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \frac{1}{3}}\end{array}} \right.\) Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ {0;\frac{1}{3}} \right\}\). |
0,25 điểm 0,25 điểm
0,25 điểm
|
|
b) Xét phương trình: \(\frac{1}{{x + 2}} + \frac{3}{{3 – x}} = \frac{{5x}}{{{x^2} – x – 6}}\) ĐK: \(x \ne – 2;x \ne 3\) \(\begin{array}{l} \Leftrightarrow \frac{{1\left( {x – 3} \right)}}{{\left( {x + 2} \right)\left( {x – 3} \right)}} – \frac{{3\left( {x + 2} \right)}}{{\left( {x + 2} \right)\left( {x – 3} \right)}} = \frac{{5x}}{{\left( {x + 2} \right)\left( {x – 3} \right)}}\\ \Leftrightarrow x – 3 – 3x – 6 = 5x\\ \Leftrightarrow – 7x = 9\end{array}\) \( \Leftrightarrow x = \frac{{ – 9}}{7}\) (thỏa mãn) Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ { – \frac{9}{7}} \right\}\). |
0,25 điểm
0,5 điểm 0,25 điểm |
|
|
c) Xét bất phương trình: \(\frac{{x + 3}}{5} – \frac{{3 – x}}{3} > \frac{{2x – 3}}{2}\) \( \Leftrightarrow \frac{{6\left( {x + 3} \right)}}{{30}} – \frac{{10\left( {3 – x} \right)}}{{30}} > \frac{{15\left( {2x – 3} \right)}}{{30}}\) \( \Leftrightarrow 6(x + 3) – 10(3 – x) > 15(2x – 3)\) \( \Leftrightarrow – 14x > – 33\) \( \Leftrightarrow x < \frac{{33}}{{14}}\) Vậy tập nghiệm của BPT: \(S = \left\{ {\left. x \right|x < \frac{{33}}{{14}}} \right\}\). |
0,5 điểm
0,25 điểm |
|
|
Câu 4 (3,5 điểm) |
– Vẽ hình đúng
a) Chứng minh \(\Delta ABH{\mathop{\rm co}\nolimits} \Delta CBA\). Xét và \(\Delta CBA\) có: \(\hat B\) là góc chung Do đó: \(\Delta ABH\,\Delta CBA(g.g)\) |
0,5 điểm
0,5 điểm
0,25 điểm |
|
b) Tính độ dài đoạn AB. Vì \(\Delta ABHco\Delta CBA(g \cdot g)\) nên ta có: \(\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\) \(\begin{array}{*{20}{l}}{ \Rightarrow A{B^2} = BC \cdot BH}\\{ \Rightarrow A{B^2} = 13.4 = 52}\\{ \Rightarrow AB = \sqrt {52} (cm)}\end{array}\) Vậy \(AB = \sqrt {52} \left( {cm} \right)\) |
0,25 điểm
0,5 điểm
0,25 điểm |
|
|
c) Ta có: Và \( \Rightarrow \widehat {EHA} = \widehat {CHF}\) Vì \( \Rightarrow \widehat {EAH} = \widehat {FCH}{\rm{ }}\) Xét \(\Delta EHA\) và \(\Delta FHC\) có: \(\widehat {EHA} = \widehat {CHF}(cmt)\) \(\widehat {EAH} = \widehat {FCH}\)(cmt) Do đó: \( \Rightarrow \frac{{AE}}{{CF}} = \frac{{AH}}{{CH}}\) \( \Rightarrow AE \cdot CH = AH \cdot FC\) |
0,25 điểm
0,25 điểm
0,25 điểm |
|
|
|
d) Xét \(\Delta ACH\) và \(\Delta BCA\) có: \(\widehat {AHC} = \widehat {BAC} = {90^0}\) \(\hat C\) là góc chung Do đó: \(\Delta ACH{\mathop{\rm co}\nolimits} \Delta BCA(g.g)\) \( \Rightarrow \frac{{AH}}{{CH}} = \frac{{AB}}{{AC}}(1)\) Vì nên \(\frac{{EH}}{{HF}} = \frac{{AH}}{{CH}}\) Từ (1) và (2) suy ra: \(\frac{{EH}}{{HF}} = \frac{{AB}}{{AC}}\) Xét \(\Delta EHF\) và \(\Delta BAC\) có: Do đó: \(\Delta EHFco\Delta BAC(\)c.g.c) \( \Rightarrow \frac{{{S_{EHF}}}}{{{S_{ABC}}}} = {\left( {\frac{{EH}}{{AB}}} \right)^2}\) \( \Rightarrow {S_{EHF}} = {S_{ABC}} \cdot {\left( {\frac{{EH}}{{AB}}} \right)^2}\) Mà \({S_{ABC}}\) và AB không đổi nên \({S_{EHF}}\) nhỏ nhất khi HE nhỏ nhất. Khi đó: \(HE \bot AB\). |
0,25 điểm
0,25 điểm |
|
Câu 5 (0,5 điểm) |
Áp dụng bất đẳng thức Cô si cho các sô dương, ta có: \(\begin{array}{l}\frac{4}{{x + 1}} + (x + 1) \ge 4\quad ;\quad \\\frac{9}{{y + 2}} + (y + 2) \ge 6\quad ;\quad \\\frac{{25}}{{z + 3}} + (z + 3) \ge 10\end{array}\) \(A + (x + y + z) + 6 \ge 20\) Vì \(x + {\rm{y}} + z = 4\) \( \Rightarrow A \ge 10\). Dấu bằng xảy ra khi \(\begin{array}{l}\left\{ \begin{array}{l}\frac{4}{{x + 1}} = x + 1\\\frac{9}{{{\rm{y}} + 2}} = {\rm{y}} + 2\\\frac{{25}}{{z + 3}} = z + 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x + 1 = 2\\{\rm{y}} + 2 = 3\\z + 3 = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 0\\{\rm{y}} = 1\\z = 2\end{array} \right.\end{array}\) Vậy \(\min A = 10\) khi \(x = 0,{\rm{y}} = 1,z = 2\). |
0,25 điểm
0,25 điểm |
———————–
Chú ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa
Bộ 21 Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2022 – 2023 – Đề 3
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề 3)
Câu 1. (2 điểm) Giải các phương trình sau :
a) 7x – 6 = 3(6 + x)
b) 4x (x + 3) = 5(x + 3)
c) \[\left| {2x – 3} \right| + x = 2\]
d) \[\frac{x}{{x + 1}} + \frac{3}{{x – 1}} = \frac{6}{{{x^2} – 1}}\]
Câu 2. (2,0 điểm) Giải các bất phương trình sau:
a) 3x + 2 \[ \ge \] 4(3x + 5)
b) \[\frac{{x – 3}}{2} < \frac{{2x – 1}}{6} – \frac{{x + 3}}{3}\]
Câu 3. (2,0 điểm) Giải bài toán sau bằng cách lập phương trình:
Một khu vườn hình chữ nhật có chiều dài gấp hai lần chiều rộng. Nếu tăng chiều rộng 4 m và giảm chiều dài 6 m thì diện tích khu vườn không thay đổi. Tìm chu vi của khu vườn lúc đầu.
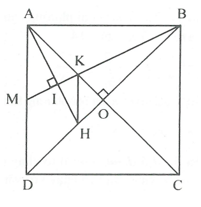
Câu 4. (4,0 điểm) Cho tam giác ABC vuông tại A có đường cao AH (H\( \in \)BC), kẻ HD vuông góc với AC tại D (D\( \in \)AC).
a) Chứng minh: ![]() DAH
DAH ![]() HAC.
HAC.
b) Gọi O là trung điểm của AB, OC cắt AH, HD lần lượt tại K và I. Chứng minh: HI = ID.
c) Chứng minh: AD.AC = BH.HC
d) Chứng minh: ba điểm B, K, D thẳng hàng.
Câu 5. (0,5 điểm) Tìm giá trị nhỏ nhất của P = x2 – 6x + 15
———-HẾT———
Đáp án
|
Câu |
Đáp án và hướng dẫn chấm |
Biểu điểm |
|
Câu 1 (2,0 điểm) |
a) Xét phương trình: \[7x–6{\rm{ }} = \;3\left( {6 + x} \right)\] \[\begin{array}{l} \Leftrightarrow 4x = 24\\ \Leftrightarrow x = 6\end{array}\] Vậy tập nghiệm của phương trình đã cho \(S = \left\{ 6 \right\}.\) |
0,5 điểm 0,25 điểm |
|
b) \[4x\left( {x + 3} \right) = 5\left( {x + 3} \right)\] \[\begin{array}{l} \Leftrightarrow 4{x^2} + 12x = 5x + 15\\ \Leftrightarrow 4{x^2} + 7x – 15 = 0\\ \Leftrightarrow 4{x^2} + 12x – 5x – 15 = 0\\ \Leftrightarrow \left( {4x – 5} \right)\left( {x + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}4x – 5 = 0\\x + 3 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{5}{4}\\x = – 3\end{array} \right.\end{array}\] Vậy tập nghiệm của phương trình: \(S = \left\{ { – 3;\frac{5}{4}} \right\}\). |
0,25 điểm
0,25 điểm
0,25 điểm |
|
|
c) \(\frac{2}{{x + 1}} – \frac{1}{{x – 2}} = \frac{{3x – 11}}{{(x + 1).(x – 2)}}\) Điều kiện xác định: \(x \ne – 1;x \ne 2.\) \( \Leftrightarrow \frac{{2\left( {x – 2} \right) – \left( {x + 1} \right)}}{{(x + 1).(x – 2)}} = \frac{{3x – 11}}{{(x + 1).(x – 2)}}\) \( \Leftrightarrow 2x – 4 – x – 1 = 3x – 11\) \( \Leftrightarrow – 2x = – 6\) \( \Leftrightarrow x = 3\) (thỏa mãn điều kiện) Vậy phương trình đã cho có tập nghiệm: \(S = \left\{ 3 \right\}\). |
0,25 điểm
0,25 điểm
0,25 điểm
|
|
|
Câu 2 (2,0 điểm) |
a) Xét BPT: \(\frac{{2x + 2}}{3} < 2 + \frac{{x – 2}}{2}\) \(\begin{array}{l} \Leftrightarrow \frac{{2\left( {2x + 2} \right)}}{6} < \frac{6}{6} + \frac{{3\left( {x – 2} \right)}}{6}\\ \Leftrightarrow 4x + 4 < 6 + 3x – 6\\ \Leftrightarrow x < – 4\end{array}\) Vậy tập nghiệm của bất phương trình: \(S = \left\{ {\left. x \right|x < – 4} \right\}\). |
0,25 điểm 0,5 điểm 0,25 điểm |
|
b) Xét bất phương trình: \(\left( {x – 3} \right)\left( {x + 3} \right) \ge {x^2} – 7x + 1\) \(\begin{array}{l} \Leftrightarrow {x^2} – 9 \ge {x^2} – 7x + 1\\ \Leftrightarrow 7x \ge 10\\ \Leftrightarrow x \ge \frac{{10}}{7}\end{array}\) Vậy tập nghiệm của bất phương trình: \(S = \left\{ {\left. x \right|x \ge \frac{{10}}{7}} \right\}\). |
0,25 điểm
0,5 điểm 0,25 điểm |
|
|
Câu 3 (2,0 điểm) |
Gọi x là độ dài quãng đường AB (\[x > 0\], đơn vị: km) Đổi 9 giờ 30 phút = 9,5 giờ Thời gian để xe máy đi hết quãng đường AB là: 9,5 – 6 = 3,5 giờ. Do đó, vận tốc của xe máy là \[\frac{x}{{3,5}}\] (km/h). Vì ô tô xuất phát sau xe máy 1 giờ, nên thời gian oto đi hết quãng đường AB là: 3,5 – 1 = 2,5 (giờ). Khi đó, vận tốc oto là: \(\frac{x}{{2,5}}\) (km/h) Vận tốc xe ôtô lớn hơn vân tốc xe máy là 20km/h. Do đó ta có phương trình: \[\frac{x}{{2,5}} – \frac{x}{{3,5}} = 20 \Leftrightarrow x = 175\] (thoả mãn) Vậy, quãng đường AB dài 175km. Vận tốc trung bình của xe máy: \[\frac{{175}}{{3,5}} = 50\] km/h. |
0,25 điểm 0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,5 điểm
0,25 điểm |
|
Câu 4 (4 điểm) |
– Vẽ hình đúng
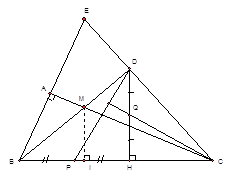
a) Chứng minh EA.EB = ED.EC Xét ∆EBD và ∆ECA có: \(\widehat {E{\rm{D}}B} = \widehat {E{\rm{A}}C} = {90^0}\) , \(\widehat {BEC}\) chung nên ∆EBD ∆ECA (g-g) Từ đó suy ra \(\frac{{EB}}{{EC}} = \frac{{ED}}{{EA}} \Rightarrow EA.EB = ED.EC\) |
0,5 điểm
0,75 điểm
0,25 điểm |
|
b) Kẻ MI vuông góc với BC (I Î BC). Xét ∆BIM và ∆BDC có: \(\widehat {BIM} = \widehat {B{\rm{D}}C} = {90^0}\) \(\widehat {MBC}\) chung \( \Rightarrow \) ∆BIM ∆BDC (g-g ) \( \Rightarrow \frac{{BM}}{{BC}} = \frac{{BI}}{{B{\rm{D}}}} \Rightarrow \)BM.BD = BC.BI (1) Tương tự: ∆ACB ∆ICM (g-g) \( \Rightarrow \frac{{CM}}{{BC}} = \frac{{CI}}{{CA}}\) \( \Rightarrow \)CM.CA = BC.CI (2) Từ (1) và (2) cộng vế với vế, suy ra:\(BM.BD + CM.CA = BI.BC + CI.BC = BC(BI + CI) = B{C^2}\)(không đổi) |
0,25 điểm
0,5 điểm
0,5 điểm
0,25 điểm |
|
|
c) Xét ∆BHD ∆DHC (g-g) Þ \(\frac{{BH}}{{DH}} = \frac{{H{\rm{D}}}}{{HC}} \Rightarrow \frac{{2.HP}}{{2.HQ}} = \frac{{H{\rm{D}}}}{{HC}} \Rightarrow \frac{{HP}}{{HQ}} = \frac{{H{\rm{D}}}}{{HC}}\) Þ∆HPD ∆HQC (c-g-c) Þ \(\widehat {PDH} = \widehat {QCH}\) mà \(\widehat {HDP} + \widehat {DPC} = {90^o}\) \( \Rightarrow \widehat {HCQ} + \widehat {DPC} = {90^o}\) \( \Rightarrow CQ \bot PD\) |
0,25 điểm
0,25 điểm
0,5 điểm |
|
|
Câu 5 (0,5 điểm) |
Ta có \[\begin{array}{l}x + y + z = 0\\ \Rightarrow x + y = – z\\ \Leftrightarrow {\left( {x + y} \right)^3} = {\left( { – z} \right)^3}\end{array}\] \[ \Leftrightarrow {x^3} + {y^3} + 3xy\left( {x + y} \right) = – {z^3}\] \[\begin{array}{l} \Leftrightarrow {x^3} + {y^3} – 3xyz = – {z^3}\\ \Leftrightarrow {x^3} + {y^3} + {z^3} = 3xyz\end{array}\](đpcm) |
0,25 điểm
0,25 điểm |
———————–
Chú ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa
Bộ 21 Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2022 – 2023 – Đề 4
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề 4)
I. Trắc nghiệm (2 điểm): Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1: Phương trình nào sau đây là phương trình bậc nhất một ẩn?
A. 0x + 25 = 0;
B. \(\frac{x}{{{x^2} – 8}} = 0\);
C. x + y = 0;
D. \(5x + \frac{1}{3} = 0\).
Câu 2: Tập nghiệm của phương trình x2 – x = 0 là:
A. S ={0};
B. S = {0; 1};
C. S = {1};
D. Một kết quả khác.
Câu 3: Bất đẳng thức nào sau đây là đúng?
A. (−5) . 3 ≤ 16;
B. (−5) + 3 ≥ 1;
C. 15 + (−3) ≥ 18 + (−3);
D. 5 . (−2) ≤ 7 . (−2).
Câu 4: Nếu ∆ABC đồng dạng với ∆A’B’C’ theo tỉ số k thì ∆A’B’C’ đồng dạng với ∆ABC theo tỉ số nào?
A. \(\frac{1}{k}\);
B. – k;
C. \(\frac{{ – \,1}}{k}\);
D. 1.
Câu 5: Nếu a < b thì . Dấu thích hợp điền vào ô trống là:
A. ≥
B. ≤
C. <
D. >
Câu 6: Hình hộp chữ nhật có chiều dài bằng 5 cm, chiều rộng bằng 3 cm, chiều cao bằng 4 cm thì có thể tích là:
A. 12 cm3;
B. 48 cm3;
C. 24 cm3.
D. 60 cm3;
II. Tự luận:
Bài 1 (3 điểm): Giải các phương trình và bất phương trình sau:
a) 2x – 3 = 0;
b) \(\frac{{x + 3}}{5} < \frac{{5 – x}}{3}\);
c) \(\frac{1}{{x – 1}} – \frac{3}{{x – 2}} = \frac{{ – 1}}{{(x – 1)(x – 2)}}\).
Bài 2 (1,5 điểm): Giải bài toán sau bằng cách lập phương trình.
Một xe máy và một ô tô cùng khởi hành từ tỉnh A đi đến tỉnh B. Xe máy đi với vận tốc 30 km/h, ô tô đi với vận tốc 40 km/h. Sau khi đi được nửa quãng đường AB, ô tô tăng vận tốc thêm 5 km/h trên quãng đường còn lại, do đó nó đến tỉnh B sớm hơn xe máy 1 giờ 10 phút. Tính độ dài quãng đường AB.
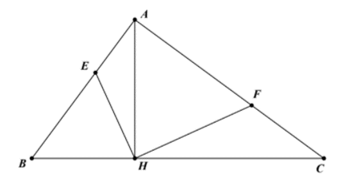
Bài 3 (2 điểm): Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh ∆AEB đồng dạng với ∆AFC. Từ đó suy ra AF . AB = AE . AC.
b) Chứng minh: \[\widehat {AEF} = \widehat {ABC}\].
c) Cho AE = 3 cm, AB = 6 cm. Chứng minh rằng SABC = 4SAEF.
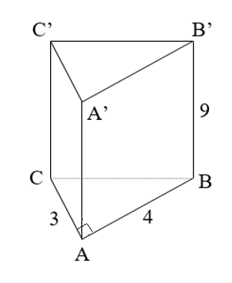
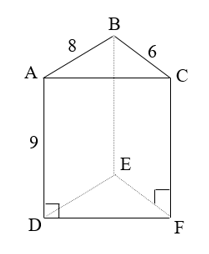
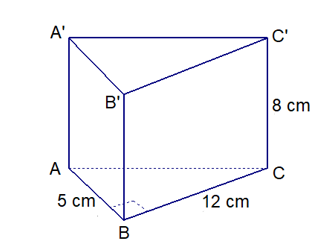
Bài 4 (1,5 điểm): Tính diện tích toàn phần và thể tích của hình lăng trụ đứng có đáy là tam giác vuông theo các kích thước ở hình sau:
Đáp án
I. Trắc nghiệm (2 điểm)
Câu 1: Phương trình nào sau đây là phương trình bậc nhất một ẩn?
A. 0x + 25 = 0;
B. \(\frac{x}{{{x^2} – 8}} = 0\);
C. x + y = 0;
D. \(5x + \frac{1}{3} = 0\).
Giải thích:
Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0.
Xét các phương trình ở các đáp án A, B, C, D:
• Phương trình 0x + 25 = 0 có hệ số a = 0 nên không phải là phương trình bậc nhất một ẩn.
• Phương trình \(\frac{x}{{{x^2} – 8}} = 0\) không có dạng ax + b = 0 nên không phải là phương trình bậc nhất một ẩn.
• Phương trình x + y = 0 có chứa hai ẩn x và y nên không phải là phương trình bậc nhất một ẩn.
• Phương trình \(5x + \frac{1}{3} = 0\) có dạng ax + b = 0 (với a = 5 ≠ 0 và \(b = \frac{1}{3}\)) nên phương trình đã cho là phương trình bậc nhất một ẩn.
Vậy chọn đáp án D.
Câu 2: Tập nghiệm của phương trình x2 – x = 0 là:
A. S ={0};
B. S = {0; 1};
C. S = {1};
D. Một kết quả khác.
Giải thích:
Ta có: x2 – x = 0
Û x(x – 1) = 0
Û x = 0 hoặc x – 1 = 0
Û x = 0 hoặc x = 1.
Do đó tập nghiệm của phương trình đã cho là S = {0; 1}.
Vậy chọn đáp án B.
Câu 3: Bất đẳng thức nào sau đây là đúng?
A. (−5) . 3 ≤ 16;
B. (−5) + 3 ≥ 1;
C. 15 + (−3) ≥ 18 + (−3);
D. 5 . (−2) ≤ 7 . (−2).
Giải thích:
Xét các bất đẳng thức ở các đáp án A, B, C, D, ta được:
• Ta có: (−5) . 3 = −15 ≤ 16. Do đó, đáp án A đúng.
• Ta có: (−5) + 3 = −2 < 1. Do đó, đáp án B sai.
• Ta có: 15 + (−3) = 15 – 3 = 12; 18 + (−3) = 18 – 3 = 15.
Vì 12 < 15 nên 15 + (−3) < 18 + (−3).
Do đó, đáp án C sai.
• Ta có: 5 . (−2) = − 10; 7 . (−2) = − 14.
Vì – 10 > − 14 nên 5 . (−2) > 7 . (−2).
Do đó, đáp án D sai.
Vậy chọn đáp án A.
Câu 4: Nếu ∆ABC đồng dạng với ∆A’B’C’ theo tỉ số k thì ∆A’B’C’ đồng dạng với ∆ABC theo tỉ số nào?
A. \(\frac{1}{k}\);
B. – k;
C. \(\frac{{ – \,1}}{k}\);
D. 1.
Giải thích:
Ta có: ∆ABC ∆A’B’C’ theo tỷ số đồng dạng k.
Hay \(\frac{{AB}}{{A’B’}} = k\).
Suy ra ∆A’B’C’ ∆ABC theo tỷ số đồng dạng \(\frac{{A’B’}}{{AB}} = \frac{1}{k}\).
Vậy chọn đáp án A.
Câu 5: Nếu a < b thì . Dấu thích hợp điền vào ô trống là:
A. ≥
B. ≤
C. <
D. >
Giải thích:
Ta có: a < b
Û 2a < 2b
Û 2a + 1 < 2b + 1.
Do đó dấu cần điền vào ô trống là <.
Vậy chọn đáp án C.
Câu 6: Hình hộp chữ nhật có chiều dài bằng 5 cm, chiều rộng bằng 3 cm, chiều cao bằng 4 cm thì có thể tích là:
A. 12 cm3;
B. 48 cm3;
C. 24 cm3.
D. 60 cm3;
Giải thích:
Thể tích của hình hộp chữ nhật là:
5 . 3 . 4 = 60 (cm3).
Vậy chọn đáp án D.
II. Tự luận:
Bài 1 (3 điểm):
a) 2x – 3 = 0
\( \Leftrightarrow \) 2x = 3
\( \Leftrightarrow x = \frac{3}{2}\).
Vậy tập nghiệm của phương trình đã cho là \(S = \left\{ {\frac{3}{2}} \right\}\).
b) \(\frac{{x + 3}}{5} < \frac{{5 – x}}{3}\)
\( \Leftrightarrow \frac{{3(x + 3)}}{{15}} < \frac{{5(5 – x)}}{{15}}\)
3(x + 3) < 5(5 – x)
3x + 9 < 25 – 5x
3x + 5x < 25 – 9
8x < 16
x < 2.
Vậy tập nghiệm của bất phương trình là {x | x < 2}.
c) \(\frac{1}{{x – 1}} – \frac{3}{{x – 2}} = \frac{{ – 1}}{{(x – 1)(x – 2)}}\).
ĐKXĐ: \(\left\{ \begin{array}{l}x – 1 \ne 0\\x – 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne 2\end{array} \right.\)
Phương trình đã cho tương đương:
\(\frac{{x – 2}}{{(x – 1)(x – 2)}} – \frac{{3(x – 1)}}{{(x – 1)(x – 2)}} = \frac{{ – 1}}{{(x – 1)(x – 2)}}\)
Suy ra: x – 2 – 3(x – 1) = –1
x – 2 – 3x + 3 = –1
x – 3x = –1 + 2 – 3
– 2x = – 2
x = 1 (không ĐKXĐ).
Vậy phương trình đã cho vô nghiệm.
Bài 2 (1,5 điểm):
Gọi x là độ dài quãng đường AB (km) (x > 0).
Đổi 1 giờ 10 phút = \(\frac{7}{6}\) giờ.
Thời gian xe máy đi hết quãng đường AB là \(\frac{x}{{30}}\) (giờ).
Thời gian ô tô đi nửa đầu quãng đường AB là: \(\frac{x}{2}:40 = \frac{x}{{80}}\) (giờ).
Vận tốc ô tô trên nửa sau quãng đường AB là: 40 + 5 = 45 (km/h).
Thời gian ô tô đi nửa sau quãng đường AB là: \(\frac{x}{2}:45 = \frac{x}{{90}}\) (giờ).
Do ô tô đến tỉnh B sớm hơn xe máy 1 giờ 10 phút nên ta có phương trình:
\(\frac{x}{{30}} = \frac{x}{{80}} + \frac{x}{{90}} + \frac{7}{6}\)
\( \Leftrightarrow \frac{{24x}}{{720}} = \frac{{9x}}{{720}} + \frac{{8x}}{{720}} + \frac{{840}}{{720}}\)
\( \Leftrightarrow \) 24x = 9x + 8x + 840
\( \Leftrightarrow \) 24x – 9x – 8x = 840
\( \Leftrightarrow \) 7x = 840
\( \Leftrightarrow \) x = 120 (TMĐK).
Vậy độ dài quãng đường AB là 120 km.
Bài 3 (2 điểm):
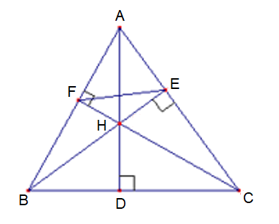
a) Xét ∆AEB và ∆AFC có:
\[\widehat {AEB} = \widehat {AFC} = {90^o}\];
\(\widehat {EAF}\) chung.
Do đó: ∆AEB đồng dạng ∆AFC (g.g).
Suy ra: \[\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}\] hay AF . AB = AE . AC.
b) Xét ∆AEF và ∆ABC có:
\(\widehat {EAF}\) chung;
\[\frac{{AF}}{{AC}} = \frac{{AE}}{{AB}}\] (do \[\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}\]).
Do đó: ∆AEF đồng dạng ∆ABC (c.g.c).
Suy ra: \[\widehat {AEF} = \widehat {ABC}\] (hai góc tương ứng).
c) Từ câu b: ∆AEF ∆ABC nên \(\frac{{AE}}{{AB}} = \frac{3}{6} = \frac{1}{2}\).
Suy ra \(\frac{{{S_{AEF}}}}{{{S_{ABC}}}} = \frac{{AE}}{{AB}} = {\left( {\frac{1}{2}} \right)^2} = \frac{1}{4}\).
Do đó SABC = 4SAEF.
Bài 4 (1,5 điểm):
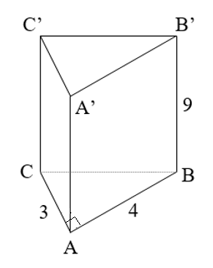
Xét ∆ABC vuông tại A, áp dụng định lý Py-ta-go, ta có:
BC2 = AB2 + AC2 = 42 + 32 = 25.
Suy ra: BC = 5 cm.
Diện tích xung quanh của hình lăng trụ đứng là:
Sxq = (3 + 4 + 5) . 9 = 108 (cm2).
Diện tích đáy của hình lăng trụ đứng là:
(cm2).
Diện tích toàn phần của hình lăng trụ là:
Stp = Sxq + S2đ = 108 + 2 . 6 = 120 (cm2).
Thể tích của hình lăng trụ đứng là:
V = Sđ . h = 6 . 9 = 54 (cm3).
Vậy hình lăng trụ đứng có diện tích toàn phần là 120 cm2 và thể tích là 54 cm3.
Bộ 21 Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2022 – 2023 – Đề 5
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề 5)
Câu 1. (2 điểm) Giải các phương trình và bất phương trình sau:
a) \(3x – 11 = x + 7\)
b) \(2x(x – 3) = x – 3\)
c) \(\frac{{x + 2}}{{x – 2}} – \frac{5}{x} = \frac{8}{{{x^2} – 2x}}\)
d) \(\frac{{2x + 1}}{4} – \frac{{x – 5}}{3} \le \frac{{4x – 1}}{{12}} + 2\)
Câu 2. (2,0 điểm) Giải bài toán sau bằng cách lập phương trình:
Một xe máy khởi hành từ A để đi đến B với vận tốc \(30\;{\rm{km}}/{\rm{h}}\). Sau khi xe máy đi được 20 phút, trên cùng tuyến đường đó, một ô tô khởi hành từ B để đi đến A với vận tốc \(45\;{\rm{km}}/{\rm{h}}\). Biết quãng đường AB dài \(90\;{\rm{km}}\). Hỏi sau bao lâu kể từ lúc ô tô khởi hành thì hai xe gặp nhau.
Câu 3. (2,0 điểm) Cho hình hộp chữ nhật \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có \(AB = 10\;{\rm{cm}};\) \(BC = 20\;{\rm{cm}};\)\(A{A^\prime } = 15\;{\rm{cm}}\):
a) Tính diện tích toàn phần của hình hộp chữ nhật.
b) Tính độ dài đường chéo \(A{C^\prime }\) của hình chộp chữ nhật (làm tròn đến chữ số thập phân thứ nhất).
Câu 4. (3,5 điểm) Cho \(\Delta ABC\) vuông tại A, đường cao AH:
a) Chứng minh \(\Delta ABH\) đồng dạng với \(\Delta CBA\).
b) Cho \(BH = 4cm,BC = 13cm.\) Tính độ dài đoạn AB.
c) Gọi E là điểm tùy ý trên cạnh AB, đường thẳng qua H và vuông góc với HE cắt cạnh AC tại F. Chứng minh AE.CH = AH.FC.
d) Tìm vị trí của điểm E trên cạnh AB để tam giác EHF có diện tích nhỏ nhất.
Câu 5. (0,5 điểm) Chứng minh rằng nếu a, b, c là các số dương và \(a + b + c = 1\) thì:
\({\left( {a + \frac{1}{a}} \right)^2} + {\left( {b + \frac{1}{b}} \right)^2} + {\left( {c + \frac{1}{c}} \right)^2} > 33\).
———-HẾT———
Đáp án
|
Câu |
Đáp án và hướng dẫn chấm |
Biểu điểm |
|
Câu 1 (2,5 điểm) |
a) \(3x – 11 = x + 7\) \( \Leftrightarrow 3x – x = 7 + 11\) \( \Leftrightarrow 2x = 18\) \( \Leftrightarrow x = 18:2\) \( \Leftrightarrow x = 9\) Vậy tập nghiệm của phương trình là \(S = \{ 9\} \). |
0,25 điểm
0,25 điểm |
|
b) \(2x(x – 3) = x – 3\) \( \Leftrightarrow 2x(x – 3) – (x – 3) = 0\) \( \Leftrightarrow (x – 3)(2x – 1) = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x – 3 = 0}\\{2x – 1 = 0}\end{array}} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 3}\\{2x = 1}\end{array}} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 3}\\{x = \frac{1}{2}}\end{array}} \right.\) Vậy tập nghiệm của phương trình là: \(S = \left\{ {3;\frac{1}{2}} \right\}\). |
0,25 điểm
0,25 điểm |
|
|
c) \(\frac{{x + 2}}{{x – 2}} – \frac{5}{x} = \frac{8}{{{x^2} – 2x}}(*)\) Điều kiện xác định: \(\left\{ {\begin{array}{*{20}{l}}{x \ne 0}\\{x – 2 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 0}\\{x \ne 2}\end{array}} \right.} \right.\) Mẫu thức chung: \({x^2} – 2x = x(x – 2)\) \((*) \Rightarrow \frac{{x(x + 2)}}{{x(x – 2)}} – \frac{{5(x – 2)}}{{x(x – 2)}} = \frac{8}{{x(x – 2)}}\) \( \Rightarrow x(x + 2) – 5(x – 2) = 8\) \( \Leftrightarrow {x^2} + 2x – 5x + 10 = 8\) \( \Leftrightarrow {x^2} – 3x + 2 = 0\) \( \Leftrightarrow {x^2} – x – 2x + 2 = 0\) \( \Leftrightarrow \left( {{x^2} – x} \right) – (2x – 2) = 0\) \( \Leftrightarrow x(x – 1) – 2(x – 1) = 0\) \( \Leftrightarrow (x – 1)(x – 2) = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x – 1 = 0}\\{x – 2 = 0}\end{array}} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1(TMDK)}\\{x = 2({\rm{ loai }})}\end{array}} \right.\) Vậy tập nghiệm của phương trình là: \(S = \{ 1\} \). |
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm |
|
|
d) \(\frac{{2x + 1}}{4} – \frac{{x – 5}}{3} \le \frac{{4x – 1}}{{12}} + 2\) \( \Leftrightarrow \frac{{3 \cdot (2x + 1)}}{{12}} – \frac{{4(x – 5)}}{{12}} \le \frac{{4x – 1}}{{12}} + \frac{{24}}{{12}}\) \( \Leftrightarrow 3 \cdot (2x + 1) – 4(x – 5) \le 4x – 1 + 24\) \( \Leftrightarrow 6x + 3 – 4x + 20 \le 4x – 1 + 24\) \( \Leftrightarrow 6x – 4x – 4x \le – 1 + 24 – 3 – 20\) \( \Leftrightarrow – 2x \le 0\) \( \Leftrightarrow x \ge 0\) Vậy tập nghiệm của bất phương trình là: \(S = \{ x\mid x \ge 0\} \). |
0,5 điểm 0,25 điểm |
|
|
Câu 2 (1,5 điểm) |
Gọi thời gian kể từ lúc ô tô khởi hành đến lúc 2 xe gặp nhau là \(x(\)giờ), điều kiện: \(x > 0\). Thời gian ô tô đi từ B đến chỗ gặp nhau là: \(x\) (giờ) Thời gian xe máy đi từ A đến chỗ gặp nhau là: \(\left( {x + \frac{1}{3}} \right)\) (giờ) Quãng đường ô tô đi được là: \(45.x(\;{\rm{km}})\) Quãng đường xe máy đi được là: \(20 \cdot \left( {x + \frac{1}{3}} \right)(km)\) Vì quãng đường AB dài \(90\;{\rm{km}}\) nên ta có phương trình: \(45x + 30 \cdot \left( {x + \frac{1}{3}} \right) = 90\) \( \Leftrightarrow 45x + 30x + 10 = 90\) \( \Leftrightarrow 75x = 90 – 10\) \( \Leftrightarrow 75x = 80\) \( \Leftrightarrow x = \frac{{80}}{{75}} = \frac{{16}}{{15}} = 1\frac{1}{{15}}\)(thỏa mãn điều kiện) Vậy thời gian kề từ lúc ô tô khởi hành đến lúc 2 xe gặp nhau là 1 giờ 4 phút. |
0,25 điểm
0,5 điểm
0,5 điểm)
0,25 điểm |
|
Câu 3 (2,0 điểm) |
a) Tính diện tích toàn phần của hình hộp chữ nhật: Chu vi đáy của hình hộp chữ nhật \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là: \(P = (AB + BC) \cdot 2 = (10 + 20) \cdot 2 = 60(\;{\rm{cm}})\) Diện tích xung quanh của hình hộp chữ nhật \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là: \({S_{xq}} = P.A{A^\prime } = 60.15 = 900\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\) Diện tích đáy của hình hộp chữ nhật \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là: \({S_d} = AB \cdot BC = 10.20 = 200\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\) Diện tích toàn phần của hình hộp chữ nhật \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là: \({S_{tp}} = {S_{xq}} + 2{S_d} = 900 + 2.200 = 1300\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\). |
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
|
|
|
b) Tính độ dài đường chéo \(A{C^\prime }\) của hình chộp chữ nhật (làm tròn đến chữ số thập phân thứ nhất). Xét \(\Delta {A^\prime }{C^\prime }{D^\prime }\) vuông tại \({D^\prime },\) theo định lí Py – ta – go, ta có: \(\begin{array}{*{20}{l}}{{A^\prime }{C^{\prime 2}} = {A^\prime }{D^{\prime 2}} + {D^\prime }{C^{\prime 2}}}\\{{A^\prime }{C^{\prime 2}} = {{20}^2} + {{10}^2}}\\{{A^\prime }{C^{\prime 2}} = 400 + 100 = 500}\end{array}\) Xét \(\Delta A{A^\prime }{C^\prime }\) vuông tại \({A^\prime },\) theo định lí Py – ta – go, ta có: \(\begin{array}{l}A{C^{\prime 2}} = A{A^{\prime 2}} + {A^\prime }{C^{\prime 2}}\\A{C^{\prime 2}} = {15^2} + 500\\A{C^{\prime 2}} = 225 + 500 = 725\\ \Rightarrow A{C^\prime } = \sqrt {725} \approx 26,9(cm)\end{array}\) Vậy độ dài đường chéo AC là 26,9 (cm). |
0,25 điểm
0,5 điểm
0,25 điểm |
|
Câu 4 (3,5 điểm) |
– Vẽ hình đúng
a) Chứng minh \(\Delta ABH{\mathop{\rm co}\nolimits} \Delta CBA\). Xét và \(\Delta CBA\) có: \(\hat B\) là góc chung Do đó: \(\Delta ABH dong dang \Delta CBA(g.g)\) |
0,5 điểm
0,5 điểm
0,25 điểm |
|
b) Tính độ dài đoạn AB. Vì nên ta có: \(\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\) \(\begin{array}{*{20}{l}}{ \Rightarrow A{B^2} = BC \cdot BH}\\{ \Rightarrow A{B^2} = 13.4 = 52}\\{ \Rightarrow AB = \sqrt {52} (cm)}\end{array}\) Vậy \(AB = \sqrt {52} \left( {cm} \right)\) |
0,25 điểm
0,5 điểm
0,25 điểm |
|
|
c) Ta có: Và \( \Rightarrow \widehat {EHA} = \widehat {CHF}\) Vì \( \Rightarrow \widehat {EAH} = \widehat {FCH}{\rm{ }}\) Xét \(\Delta EHA\) và \(\Delta FHC\) có: \(\widehat {EHA} = \widehat {CHF}(cmt)\) \(\widehat {EAH} = \widehat {FCH}\)(cmt) Do đó: \( \Rightarrow \frac{{AE}}{{CF}} = \frac{{AH}}{{CH}}\) \( \Rightarrow AE \cdot CH = AH \cdot FC\) |
0,25 điểm
0,25 điểm
0,25 điểm |
|
|
|
d) Xét \(\Delta ACH\) và \(\Delta BCA\) có: \(\widehat {AHC} = \widehat {BAC} = {90^0}\) \(\hat C\) là góc chung Do đó: \( \Rightarrow \frac{{AH}}{{CH}} = \frac{{AB}}{{AC}}(1)\) Vì \(\Delta EHA dong dang \Delta FHC(g.g)\) nên \(\frac{{EH}}{{HF}} = \frac{{AH}}{{CH}}\) Từ (1) và (2) suy ra: \(\frac{{EH}}{{HF}} = \frac{{AB}}{{AC}}\) Xét \(\Delta EHF\) và \(\Delta BAC\) có: Do đó: \( \Rightarrow \frac{{{S_{EHF}}}}{{{S_{ABC}}}} = {\left( {\frac{{EH}}{{AB}}} \right)^2}\) \( \Rightarrow {S_{EHF}} = {S_{ABC}} \cdot {\left( {\frac{{EH}}{{AB}}} \right)^2}\) Mà \({S_{ABC}}\) và AB không đổi nên \({S_{EHF}}\) nhỏ nhất khi HE nhỏ nhất. Khi đó: \(HE \bot AB\). |
0,25 điểm
0,25 điểm |
|
Câu 5 (0,5 điểm) |
Với ba số \(A > 0;B > 0;C > 0\). Áp dụng bất đẳng thức Cauchy, ta có: \(\left. {\begin{array}{*{20}{l}}{{A^2} + {B^2} \ge 2AB}\\{{B^2} + {C^2} \ge 2BC}\\{{A^2} + {C^2} \ge 2AC}\end{array}} \right\} \Rightarrow 2\left( {{A^2} + {B^2} + {C^2}} \right) \ge 2(AB + BC + AC)\) Cộng từng vế của bất đẳng thức trên với \({A^2} + {B^2} + {C^2},\) ta được:\(\begin{array}{l}3\left( {{A^2} + {B^2} + {C^2}} \right) \ge 2(AB + BC + AC) + {{\rm{A}}^2} + {B^2} + {C^2}\\ \Rightarrow 3\left( {{A^2} + {B^2} + {C^2}} \right) \ge {(A + B + C)^2}\\ \Rightarrow {A^2} + {B^2} + {C^2} \ge \frac{{{{(A + B + C)}^2}}}{3}\end{array}\) Đặt \(A = a + \frac{1}{a};B = b + \frac{1}{b};C = c + \frac{1}{c}\) và vế trái là \(P\), ta được: \(\begin{array}{l}P \ge \frac{1}{3} \cdot {\left( {a + \frac{1}{a} + b + \frac{1}{b} + c + \frac{1}{c}} \right)^2}\\ = \frac{1}{3}{\left( {a + b + c + \frac{{a + b + c}}{a} + \frac{{a + b + c}}{b} + \frac{{a + b + c}}{c}} \right)^2}\end{array}\) \( \Rightarrow P \ge \frac{1}{3}{\left( {1 + 1 + \frac{b}{a} + \frac{c}{a} + 1 + \frac{a}{b} + \frac{c}{b} + 1 + \frac{a}{c} + \frac{b}{c}} \right)^2}\) \( \Rightarrow P \ge \frac{1}{3}{\left( {1 + 1 + 1 + 1 + \frac{b}{a} + \frac{a}{b} + \frac{c}{a} + \frac{a}{c} + \frac{c}{b} + \frac{b}{c}} \right)^2}\) Áp dụng bất đẳng thức Cauchy cho hai số dương \(\frac{a}{b}\) và \(\frac{b}{a},\) ta được: \(\frac{a}{b} + \frac{b}{a} \ge 2\sqrt {\frac{a}{b} \cdot \frac{b}{a}} = 2\) Tương tự: \(\frac{a}{c} + \frac{c}{a} \ge 2\sqrt {\frac{a}{c} \cdot \frac{c}{a}} = 2;\frac{b}{c} + \frac{c}{b} \ge 2\sqrt {\frac{b}{c} \cdot \frac{c}{b}} = 2\) Khi đó, \(P \ge \frac{1}{3}{(1 + 1 + 1 + 1 + 6)^2} = \frac{1}{3} \cdot {10^2} = \frac{{100}}{3} > 33\) Vậy \({\left( {a + \frac{1}{a}} \right)^2} + {\left( {b + \frac{1}{b}} \right)^2} + {\left( {c + \frac{1}{c}} \right)^2} > 33\). |
0,25 điểm
0,25 điểm |
———————–
Chú ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa
Bộ 21 Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2022 – 2023 – Đề 6
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề 6)
I. Trắc nghiệm (2 điểm): Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1: Hình hộp chữ nhật là hình có bao nhiêu mặt?
A. 6 đỉnh , 8 mặt , 12 cạnh;
B. 8 đỉnh , 6 mặt , 12 cạnh;
C. 12 đỉnh , 6 mặt , 8 cạnh;
D. 6 đỉnh , 12 mặt , 8 cạnh.
Câu 2: Điều kiện xác định của phương trình \(\frac{{x + 2}}{{x – 3}} = \frac{{3x – 1}}{{x(x – 3)}} + 1\) là:
A. x ≠ 0 hoặc x ≠ 3;
B. x ≠ 0 hoặc x ≠ −3;
C. x ≠ 0 và x ≠ 3;
D. x ≠ 3.
Câu 3: Tập nghiệm của phương trình x(x + 1) = 0 là:
A. S = {–1};
B. S = {0; –1};
C. S = {0};
D. S = {1; 0}.
Câu 3: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
A. x + y > 8;
B. 0x + 5 ≥ 0;
C. x – 3 > 4 ;
D. (x – 7)2 ≤ 6x.
Câu 4. Hình sau biểu diễn tập nghiệm của bất phương trình nào?

A. x ≥ 2;
B. x 2;
C. x > 2;
D. x < 2.
Câu 6: Trong các khẳng định sau, khẳng định nào không đúng?
A. Hình hộp chữ nhật là hình lăng trụ đứng;
B. Các mặt bên của hình lăng trụ đứng là hình chữ nhật;
C. Các cạnh bên của hình lăng trụ đứng không bằng nhau;
D. Hình lăng trụ đứng có đáy là hình bình hành gọi là hình hộp đứng.
II. Tự luận:
Bài 1 (1,5 điểm): Giải các phương trình và bất phương trình sau:
a) (x – 2)(x + 7) = 0;
b) \[\frac{{4x + 7}}{{18}} – \frac{{5x}}{3} \ge \frac{1}{2}\].
Bài 2 (2 điểm): Giải bài toán bằng cách lập phương trình.
Một vòi nước chảy vào bể không có nước. Cùng lúc đó một vòi nước khác chảy từ bể ra. Mỗi giờ lượng nước vòi chảy ra bằng \(\frac{4}{5}\) lượng nước chảy vào. Sau 5 giờ thì bên trong bể đạt tới \(\frac{1}{8}\) dung tích bể. Hỏi nếu bể không có nước mà chỉ mở vòi chảy vào thì sau bao lâu thì đầy bể?
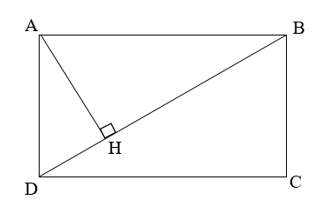
Bài 3 (3 điểm): Cho hình chữ nhật ABCD có AB = 8 cm; BC = 6 cm. Vẽ đường cao AH của ∆ADB.
a) Chứng minh: ∆AHB đồng dạng ∆BCD.
b) Chứng minh: AD2 = DH . DB.
c) Tính độ dài đoạn thẳng AH.
Bài 4 (1,5 điểm): Cho hình lăng trụ đứng ABC.DEF (như hình vẽ) có đáy là tam giác vuông, biết độ dài hai cạnh góc vuông là 6 cm và 8 cm; chiều cao của lăng trụ là 9 cm. Tính diện tích toàn phần của hình lăng trụ?
Đáp án
c. Trắc nghiệm (2 điểm):
Câu 1: Hình hộp chữ nhật là hình có bao nhiêu mặt?
A. 6 đỉnh , 8 mặt , 12 cạnh;
B. 8 đỉnh , 6 mặt , 12 cạnh;
C. 12 đỉnh , 6 mặt , 8 cạnh;
D. 6 đỉnh , 12 mặt , 8 cạnh.
Giải thích:
Hình hộp chữ nhật là hình gồm có 8 đỉnh , 6 mặt , 12 cạnh.
Vậy chọn đáp án B.
Câu 2: Điều kiện xác định của phương trình \(\frac{{x + 2}}{{x – 3}} = \frac{{3x – 1}}{{x(x – 3)}} + 1\) là:
A. x ≠ 0 hoặc x ≠ 3;
B. x ≠ 0 hoặc x ≠ −3;
C. x ≠ 0 và x ≠ 3;
D. x ≠ 3.
Giải thích:
Điều kiện xác định: \[\left\{ \begin{array}{l}x \ne 0\\x – 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne 3\end{array} \right.\]
Vậy chọn đáp án C.
Câu 3: Tập nghiệm của phương trình x(x + 1) = 0 là:
A. S = {–1};
B. S = {0; –1};
C. S = {0};
D. S = {1; 0}.
Giải thích:
Ta có : x(x + 1) = 0
x = 0 hoặc x + 1 = 0
x = 0 hoặc x = − 1.
Do đó, tập nghiệm của phương trình đã cho là S = {0 ; –1}.
Vậy chọn đáp án B.
Câu 3: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
A. x + y > 8 ;
B. 0x + 5 ≥ 0 ;
C. x – 3 > 4 ;
D. (x – 7)2 ≤ 6x.
Giải thích :
Bất phương trình ẩn x là hệ thức A (x) > B (x) hoặc A (x) < B (x) hoặc A (x) ≥ B (x) hoặc A (x) ≤ B (x). Trong đó : A (x) gọi là vế trái ; B(x) gọi là vế phải.
Ta có :
• Bất phương trình x + y > 8 có vế trái là đa thức có chứa hai ẩn, vế phải là hằng số.
Do đó, x + y > 8 không phải là bất phương trình bậc nhất một ẩn.
• Bất phương trình 0x + 5 ≥ 0 có vế trái là hằng số (vì 0x + 5 = 5) và vế phải cũng là hằng số.
Do đó, 0x + 5 ≥ 0 không phải là bất phương trình bậc nhất một ẩn.
• Bất phương trình x – 3 > 4 có vế trái là đa thức bậc nhất một ẩn, vế phải là hằng số.
Do đó, x – 3 > 4 là bất phương trình bậc nhất một ẩn.
• Bất phương trình (x – 7)2 ≤ 6x có vế phải là đa thức bậc hai, vế phải là hằng số.
Do đó, (x – 7)2 ≤ 6x là bất phương trình bậc nhất một ẩn.
Vậy chọn đáp án C.
Câu 4. Hình sau biểu diễn tập nghiệm của bất phương trình nào?

A. x ≥ 2;
B. x 2;
C. x > 2;
D. x < 2.
Giải thích:
Hình vẽ trên biểu diễn tập nghiệm của bất phương trình x 2.
Vậy chọn đáp án B.
Câu 6: Trong các khẳng định sau, khẳng định nào không đúng?
A. Hình hộp chữ nhật là hình lăng trụ đứng;
B. Các mặt bên của hình lăng trụ đứng là hình chữ nhật;
C. Các cạnh bên của hình lăng trụ đứng không bằng nhau;
D. Hình lăng trụ đứng có đáy là hình bình hành gọi là hình hộp đứng.
Giải thích:
Các khẳng định A, B, D là khẳng định đúng.
Còn khẳng định C sai vì các cạnh bên của hình lăng trụ đứng bằng nhau.
Vậy chọn đáp án C.
II. Tự luận:
Bài 1 (1,5 điểm):
c) (x – 2)(x + 7) = 0
x – 2 = 0 hoặc x + 7 = 0
x = 2 hoặc x = −7.
Vậy tập nghiệm của phương trình đã cho là S = {2; −7}.
b) \[\frac{{4x + 7}}{{18}} – \frac{{5x}}{3} \ge \frac{1}{2}\]
\[ \Leftrightarrow \frac{{4x + 7}}{{18}} – \frac{{30x}}{{18}} \ge \frac{9}{{18}}\]
4x + 7 – 30x ≥ 9
4x – 30x ≥ 9 – 7
– 26x ≥ 2
\( \Leftrightarrow x \le \frac{{ – \,\,1}}{{13}}\).
Vậy tập nghiệm của bất phương trình đã cho là \(S = \left\{ {x|x \le \frac{{ – \,\,1}}{{13}}} \right\}\).
Bài 2 (2 điểm):
Gọi x (giờ) là thời gian vòi chảy vào bể từ khi chưa có nước đến khi đầy bể (x > 0).
Trong 1 giờ, vòi đó chảy được số phần bể là: \[\frac{1}{x}\] bể.
Trong 1 giờ, vòi chảy ra chiếm số phần bể là: \[\frac{1}{x}\,\,.\,\,\frac{4}{5} = \frac{4}{{5x}}\] bể.
Sau 5 giờ thì bên trong bể đạt tới \(\frac{1}{8}\) dung tích bể nên ta có phương trình:
\[5\,.\,\,\left( {\frac{1}{x} – \frac{4}{{5x}}} \right) = \frac{1}{8}\]
\[ \Leftrightarrow \frac{5}{x} – \frac{4}{x} = \frac{1}{8}\]
\[ \Leftrightarrow \frac{1}{x} = \frac{1}{8}\]
\( \Leftrightarrow \) x = 8 (TMĐK).
Vậy thời gian vòi chảy vào bể từ khi chưa có nước đến khi đầy bể là 8 giờ.
Bài 3 (3 điểm):
c) Vì ABCD là hình chữ nhật nên AB // CD.
Suy ra: \(\widehat {ABH} = \widehat {BDC}\) (hai góc so le trong).
Xét ∆AHB và ∆BCD có:
\(\widehat {AHB} = \widehat {BCD} = {90^o}\)
\(\widehat {ABH} = \widehat {BDC}\) (cmt).
Do đó ∆AHB ∆BCD (g.g).
b) Xét ∆AHD và ∆BAD có:
\(\widehat {AHD} = \widehat {BAD} = {90^o}\)
\(\widehat {ADB}\) chung.
Do đó ∆AHD đồng dạng ∆BAD (g.g)
Suy ra \(\frac{{AD}}{{BD}} = \frac{{DH}}{{DA}}\).
Vậy AD2 = DH . BD (đpcm).
c) Xét ∆ABD vuông tại A, áp dụng định lý Py-ta-go, ta có:
BD2 = AB2 + AD2 = 82 + 62 = 100
Suy ra: BD = 10 (cm)
Từ câu a: ∆AHB đồng dạng ∆BCD suy ra \(\frac{{AH}}{{BC}} = \frac{{AB}}{{BD}}\).
Hay AH . BD = AB. BC.
Do đó \(AH = \frac{{AB\,.\,BC}}{{BD}} = \frac{{8\,.\,6}}{{10}} = 4,8\) (cm).
Vậy AH = 4,8 cm.
Bài 4 (1,5 điểm):
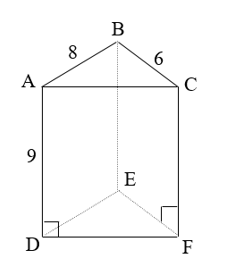
Độ dài hai cạnh góc vuông là 6 cm và 8 cm nên ∆ABC vuông tại B.
Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{8^2} + {6^2}} = 10\) (theo định lý Py-ta-go).
Diện tích xung quanh của hình lăng trụ đứng là:
Sxq = (6 + 8 + 10) . 9 = 216 (cm2).
Diện tích một mặt đáy của hình lăng trụ đứng là:
(cm2).
Diện tích toàn phần của hình lăng trụ đứng là:
Stp = Sxq + S2đ = 216 + 2 . 24 = 264 (cm2).
Vậy diện tích toàn phần của hình lăng trụ 264 cm2.
Bộ 21 Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2022 – 2023 – Đề 7
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề 7)
Câu 1. (2,0 điểm) Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) \(3\left( {2x – 7} \right) + 2x > 4\left( {x + 2} \right) – 25\)
b) \(\frac{{3x – 8}}{5} – 1 \ge \frac{{2x – 3}}{3} + x\)
Câu 2. (1,5 điểm) Giải bài toán sau bằng cách lập phương trình:
Một xe gắn máy đi đoạn đường từ A đến B dài 70km. Lúc về, chiếc xe ấy đi bằng đường khác dài 84km với vận tốc kém hơn lượt đi là 8km/h. Tính vận tốc lúc về biết thời gian về gấp \(\frac{3}{2}\) thời gian lúc đi.
Câu 3. (2,5 điểm) Giải các phương trình:
a) \({\left( {x + 5} \right)^2} + 137 = x\left( {x – 4} \right) – 4x\)
b) \(\left| {x – 2014} \right| = 2014x\)
c) \(\frac{4}{{x + 2}} – \frac{{4x – 6}}{{4x – {x^3}}} = \frac{{x – 3}}{{x\left( {x – 2} \right)}}\)
Câu 4. (3,5 điểm) Cho hình vuông ABCD. Gọi M là trung điểm của AD, kẻ AI vuông góc với MB tại I
a) Chứng minh \(\Delta AMB\) và \(\Delta IMA\) đồng dạng
b) Gọi O là giao điểm của AC và BD. Chứng minh: \(OC.BD = BC.DC\)
c) BM cắt AC tại K; AI cắt BD tại H. Chứng minh: \(BH = 2DH\)
d) Cho \(AM = 30cm\). Tính diện tích \(\Delta AIB\)
Câu 5. (0,5 điểm) Cho a, b, c là ba số dương thỏa mãn \[abc = 1\].
Chứng minh rằng: \[\frac{1}{{{a^3}\left( {b + c} \right)}} + \frac{1}{{{b^3}\left( {c + a} \right)}} + \frac{1}{{{c^3}\left( {a + b} \right)}} \ge \frac{3}{2}\].
———-HẾT———
Đáp án
|
Câu |
Đáp án và hướng dẫn chấm |
Biểu điểm |
|
Câu 1 (2,0 điểm) |
a) \(3\left( {2x – 7} \right) + 2x > 4\left( {x + 2} \right) – 25\) \(\begin{array}{l} \Leftrightarrow 6x – 21 + 2x > 4x + 8 – 25\\ \Leftrightarrow 8x – 21 > 4x – 17\end{array}\) \(\begin{array}{l} \Leftrightarrow 8x – 4x > – 17 + 21\\ \Leftrightarrow 4x > 4\\ \Leftrightarrow x > 1\end{array}\) Vậy tập nghiệm của bất phương trình là : \(S = \left\{ {x\left| {x > 1} \right.} \right\}\) Biểu diễn tập nghiệm trên trục số
|
0,5 điểm
0,25 điểm
0,25 điểm |
|
b) \(\frac{{3x – 8}}{5} – 1 \ge \frac{{2x – 3}}{3} + x\) \( \Leftrightarrow 3\left( {3x – 8} \right) – 15 \ge 5\left( {2x – 3} \right) + 15x\) \( \Leftrightarrow 9x – 24 – 15 \ge 10x – 15 + 15x\) \( \Leftrightarrow 9x – 39 \ge 25x – 15\) \(\begin{array}{l} \Leftrightarrow 9x – 25x \ge – 15 + 39\\ \Leftrightarrow – 16x \ge 24\\ \Leftrightarrow x \le – \frac{3}{2}\end{array}\) Vậy tập nghiệm của bất phương trình là: \(S = \left\{ {x\left| {x \le – \frac{3}{2}} \right.} \right\}\) Biểu diễn tập nghiệm trên trục số
|
0,5 điểm
0,25 điểm
0,25 điểm |
|
|
Câu 2 (1,5 điểm) |
Gọi vận tốc lúc về là x(km/h) (điều kiện x > 0) Vận tốc lúc đi là: x+8 (km/h) Thời gian đi từ B về A là: \(\frac{{84}}{x}\) (h) Thời gian đi từ A đến B là: \(\frac{{70}}{{x + 8}}\) (h) Theo đầu bài, ta có phương trình \(\frac{{84}}{x} = \frac{3}{2}.\frac{{70}}{{x + 8}}\) \(\begin{array}{l} \Leftrightarrow \frac{{84}}{x} = \frac{{105}}{{x + 8}}\\ \Leftrightarrow 105x = 84\left( {x + 8} \right)\\ \Leftrightarrow 105x = 84x + 672\\ \Leftrightarrow 21x = 672\end{array}\) \( \Leftrightarrow x = 672:21 \Leftrightarrow x = 32\) (thích hợp) Vậy vận tốc lúc về là 32km/h |
0,25 điểm
0,5 điểm
0,5 điểm)
0,25 điểm |
|
Câu 3 (2,5 điểm) |
a) \({\left( {x + 5} \right)^2} + 137 = x\left( {x – 4} \right) – 4x\) \(\begin{array}{l} \Leftrightarrow {x^2} + 10x + 25 + 137 = {x^2} – 4x – 4x\\ \Leftrightarrow {x^2} + 10x + 162 = {x^2} – 8x\end{array}\) \(\begin{array}{l}{x^2} + 10x – {x^2} + 8x = – 162\\ \Leftrightarrow 18x = – 162\\ \Leftrightarrow x = – 162:18 \Leftrightarrow x = 9\end{array}\) Vậy tập nghiệm của phương trình là: \(S = \left\{ 9 \right\}\) |
0,5 điểm
0,5 điểm |
|
b) \(\left| {x – 2014} \right| = 2014x\) (*), ĐKXĐ: \(x \ge 0\) Nếu \(x \ge 2014\) thì \(\left| {x – 2014} \right| = x – 2014\) Do đó: (*) \( \Leftrightarrow x – 2014 = 2014x\) \( \Leftrightarrow x – 2014x = 2014 \Leftrightarrow – 2013x = 2014 \Leftrightarrow x = \frac{{ – 2014}}{{2013}}\) (loại) Nếu x < 2014 thì \(\left| {x – 2014} \right| = 2014 – x\) Do đó: (*) \( \Leftrightarrow 2014 – x = 2014x\) \( \Leftrightarrow – x – 2014x = – 2014 \Leftrightarrow – 2015x = – 2014 \Leftrightarrow x = \frac{{2014}}{{2015}}\) (nhận) Vậy tập nghiệm của phương trình là: \(S = \left\{ {\frac{{2014}}{{2015}}} \right\}\). |
0,25 điểm
0,25 điểm
0,25 điểm |
|
|
c) \(\frac{4}{{x + 2}} – \frac{{4x – 6}}{{4x – {x^3}}} = \frac{{x – 3}}{{x\left( {x – 2} \right)}}\) \( \Leftrightarrow \frac{4}{{x – 2}} + \frac{{4x – 6}}{{x\left( {x + 2} \right)\left( {x – 2} \right)}} = \frac{{x – 3}}{{x\left( {x – 2} \right)}}\) ĐKXĐ: \(x \ne 0,\,\,x \ne 2,\,x \ne – 2\) Phương trình trở thành \(4x\left( {x – 2} \right) + 4x – 6 = \left( {x – 3} \right)\left( {x + 2} \right)\) \( \Leftrightarrow 4{x^2} – 8x + 4x – 6 = {x^2} + 2x – 3x – 6 \Leftrightarrow 4{x^2} – 4x – 6 = {x^2} – x – 6\) \( \Leftrightarrow 4{x^2} – 4x – 6 – {x^2} + x + 6 = 0 \Leftrightarrow 3{x^2} – 3x = 0\) \( \Leftrightarrow 3x\left( {x – 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x – 1 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0\,(KTM)}\\{x = 1\,(TM)}\end{array}} \right.} \right.\) Vậy tập nghiệm của phương trình là: \(S = \left\{ 1 \right\}\). |
0,25 điểm
0,25 điểm
0,25 điểm
|
|
|
Câu 4 (3,5 điểm) |
– Vẽ hình đúng
a) Xét \(\Delta AMB\) và \(\Delta IMA\) có: \(\widehat {AMB}\) (chung), \(\widehat {MAB} = \widehat {MIA}\,\left( { = 90^\circ } \right)\) Do đó \(\Delta AMB \sim \Delta IMA\) (g.g) |
0,5 điểm
0,5 điểm
|
|
b) Tứ giác ABCD là hình vuông \( \Rightarrow AC \bot BD,\,OB = OD\) Ta có: \({S_{BCD}} = \frac{1}{2}OC.BD\,\,(OC \bot BD)\) Và \({S_{BCD}} = \frac{1}{2}BC.DC\,\,(BC \bot CD)\) Suy ra \(OC.BD = BC.DC\). |
0,25 điểm
0,5 điểm
0,25 điểm |
|
|
c) \(\Delta ABH\) có AO, BI là hai đường cao cắt nhau tại K \( \Rightarrow \)K là trực tâm của tam giác ABH \( \Rightarrow \) HK là đường cao của tam giác ABH \( \Rightarrow HK \bot AB\). Mà \(AD \bot AB\) Do đó \(HK//AD\) \(\Delta ABD\) có AO, BM là hai đường trung tuyến cắt nhau tại K \( \Rightarrow \)K là trọng tâm của tam giác ABD \( \Rightarrow BK = \frac{2}{3}BM \Rightarrow \frac{{BK}}{{BM}} = \frac{2}{3}\) \(\Delta BMD\) có \(KH//MD \Rightarrow \frac{{BH}}{{BD}} = \frac{{BK}}{{BM}} = \frac{2}{3} \Rightarrow BH = \frac{2}{3}BD\) Nên \(BH = 2DH\). |
0,5 điểm
0,25 điểm
0,25 điểm |
|
|
d) Xét \(\Delta ABM\) và \(\Delta IBA\) có; \(\widehat {BAM} = \widehat {BIA}\,\left( { = 90^\circ } \right)\), \(\widehat {ABM}\) (chung) Do đó \(\Delta ABM \sim \Delta IBA\) (g.g) \( \Rightarrow \frac{{AB}}{{IB}} = \frac{{AM}}{{IA}} \Rightarrow \frac{{IA}}{{IB}} = \frac{{AM}}{{AB}}\) Mà \(\frac{{AM}}{{AB}} = \frac{{AM}}{{AD}} = \frac{1}{2}\). Nên \(\frac{{IA}}{{IB}} = \frac{1}{2} \Rightarrow IB = 2IA\) \(AB = 2AM = 2.30 = 60\,\left( {cm} \right)\) \(\Delta IAB\) vuông tại I \( \Rightarrow I{A^2} + I{B^2} = A{B^2}\) \( \Rightarrow I{A^2} + 4I{A^2} = {60^2} \Rightarrow I{A^2} = \frac{{{{60}^2}}}{5} = 720\) \({S_{AIB}} = \frac{1}{2}IA.IB = \frac{1}{2}IA.2IA = I{A^2} = 720\,\left( {c{m^2}} \right)\) |
0,25 điểm
0,25 điểm |
|
|
Câu 5 (0,5 điểm) |
Với \[\forall a,b,c \in \mathbb{R}\] và \[x,y,x > 0\] chứng minh rằng: \[\frac{{{a^2}}}{x} + \frac{{{b^2}}}{y} + \frac{{{c^2}}}{z} \ge \frac{{{{\left( {a + b + c} \right)}^2}}}{{x + y + z}}{\rm{ }}\left( * \right)\] Dấu xảy ra \[ \Leftrightarrow \frac{a}{x} = \frac{b}{y} = \frac{c}{z}\] Thật vậy, với \[a,b \in \mathbb{R}\] và \[x,y > 0\] ta có \[\frac{{{a^2}}}{x} + \frac{{{b^2}}}{y} \ge \frac{{{{\left( {a + b} \right)}^2}}}{{x + y}}{\rm{ }}\left( {**} \right)\] \[ \Leftrightarrow \left( {{a^2}{y^{}} + {b^2}x} \right)\left( {x + y} \right) \ge xy{\left( {a + b} \right)^2} \Leftrightarrow {\left( {bx – ay} \right)^2} \ge 0\](luôn đúng) Dấu xảy ra \[ \Leftrightarrow \frac{a}{x} = \frac{b}{y}\] Áp dụng bất đẳng thức (**) ta có: \[\frac{{{a^2}}}{x} + \frac{{{b^2}}}{y} + \frac{{{c^2}}}{z} \ge \frac{{{{\left( {a + b} \right)}^2}}}{{x + y}} + \frac{{{c^2}}}{z} \ge \frac{{{{\left( {a + b + c} \right)}^2}}}{{x + y + z}}\] Dấu xảy ra \[ \Leftrightarrow \frac{a}{x} = \frac{b}{y} = \frac{c}{z}\] Ta có \[\frac{1}{{{a^3}\left( {b + c} \right)}} + \frac{1}{{{b^3}\left( {c + a} \right)}} + \frac{1}{{{c^3}\left( {a + b} \right)}} = \frac{{\frac{1}{{{a^2}}}}}{{ab + ac}} + \frac{{\frac{1}{{{b^2}}}}}{{bc + ab}} + \frac{{\frac{1}{{{c^2}}}}}{{ac + bc}}\] Áp dụng bất đẳng thức (*) ta có: \[\frac{{\frac{1}{{{a^2}}}}}{{ab + ac}} + \frac{{\frac{1}{{{b^2}}}}}{{bc + ab}} + \frac{{\frac{1}{{{c^2}}}}}{{ac + bc}} \ge \frac{{{{\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right)}^2}}}{{2\left( {ab + bc + ac} \right)}} = \frac{{{{\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right)}^2}}}{{2\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right)}}\] (Vì \[abc = 1\]) Hay \[\frac{{\frac{1}{{{a^2}}}}}{{ab + ac}} + \frac{{\frac{1}{{{b^2}}}}}{{bc + ab}} + \frac{{\frac{1}{{{c^2}}}}}{{ac + bc}} \ge \frac{1}{2}\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right)\] Mà \[\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \ge 3\] nên \[\frac{{\frac{1}{{{a^2}}}}}{{ab + ac}} + \frac{{\frac{1}{{{b^2}}}}}{{bc + ab}} + \frac{{\frac{1}{{{c^2}}}}}{{ac + bc}} \ge \frac{3}{2}\] Vậy \[\frac{1}{{{a^3}\left( {b + c} \right)}} + \frac{1}{{{b^3}\left( {c + a} \right)}} + \frac{1}{{{c^3}\left( {a + b} \right)}} \ge \frac{3}{2}\](đpcm)
|
0,25 điểm
0,25 điểm |
———————–
Chú ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa
Bộ 21 Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2022 – 2023 – Đề 8
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề 8)
Câu 1. (2 điểm) Giải các phương trình sau:
a) \(\frac{x}{{2016}} + \frac{{x + 1}}{{2015}} + \frac{{x + 14}}{{2002}} + 3 = 0\)
b) \(\left( {5x – 9} \right)\left( {{x^2} – 5x + 4} \right) = \left( {5x – 9} \right)\left( {3x – 12} \right)\)
c) \(\frac{1}{{x – 2}} + \frac{2}{{x – 4}} = – 1\)
Câu 2. (2 điểm) Giải các bất phương trình sau:
a)\(8x – 1 > 5x – 7\)
b) \(\frac{{{x^2} – 4}}{6} – \frac{{x – 1}}{3} \le 1\)
c) \({\left( {x + 3} \right)^2} – {x^2} – 3x > 8\)
Câu 3. (1,5 điểm) Tìm số tự nhiên có hai chữ số, biết rằng tổng hai chữ số là 11 và nếu đổi chỗ hai chữ số cho nhau thì thu được số mới lớn hơn số ban đầu là 27.
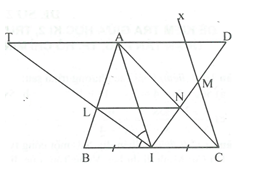
Câu 4. (4 điểm) Cho tam giác ABC có đường trung tuyến AI và IL là đường phân giác trong của tam giác AIB. Từ L kẻ đường thẳng song song với BC cắt AC tại N.
a) Chứng minh rằng \(\frac{{LA}}{{LB}} = \frac{{IA}}{{IC}}\)
b) Vẽ tia Cx song song với IA cắt đường thẳng IN tại M. Chứng minh rằng: \(NA.MC = AI.NC\).
c) Chứng minh rằng: tam giác ICM cân tại C và IN là tia phân giác của góc AIC.
d) Đường thẳng qua A song song với BC lần lượt cắt các đường thẳng IL, IN tại T và D. Chứng minh rằng: \(TD = 2AI\).
Câu 5. (0.5 điểm) Một công ty cần vận chuyển một lô hàng hóa gồm 7 thùng hàng A và 4 thùng hàng B bằng các xe chuyên dụng. Hỏi công ty này cần sử dụng bao nhiêu chiếc xe chuyên dụng để vận chuyển hết lô hàng hóa đó cùng một lúc? Biết rằng mỗi thùng hàng A nặng 450kg, mỗi thùng hàng B nặng 300kg và mỗi xe chuyên dụng chỉ chở được tối đa 1 tấn hàng hóa.
———-HẾT———
Đáp án
|
Câu |
Đáp án và hướng dẫn chấm |
Biểu điểm |
|
Câu 1 (2,0 điểm) |
a) \(\frac{x}{{2016}} + \frac{{x + 1}}{{2015}} + \frac{{x + 14}}{{2002}} + 3 = 0\) \( \Leftrightarrow \left( {\frac{x}{{2016}} + 1} \right) + \left( {\frac{{x + 1}}{{2015}} + 1} \right) + \left( {\frac{{x + 14}}{{2002}} + 1} \right) = 0\) \( \Leftrightarrow \frac{{x + 2016}}{{2016}} + \frac{{x + 2016}}{{2015}} + \frac{{x + 2016}}{{2002}} = 0\) \( \Leftrightarrow \left( {x + 2016} \right)\left( {\frac{1}{{2016}} + \frac{1}{{2015}} + \frac{1}{{2002}}} \right) = 0\) \( \Leftrightarrow x + 2016 = 0\) (vì \(\left( {\frac{1}{{2016}} + \frac{1}{{2015}} + \frac{1}{{2002}}} \right) \ne 0\)) \( \Leftrightarrow x = – 2016\) Vậy tập nghiệm của phương trình là : \(S = \left\{ { – 2016} \right\}\) |
0,25 điểm
0,25 điểm
0,25 điểm |
|
b) \(\left( {5x – 9} \right)\left( {{x^2} – 5x + 4} \right) = \left( {5x – 9} \right)\left( {3x – 12} \right)\) \( \Leftrightarrow \left( {5x – 9} \right)\left( {{x^2} – 5x + 4} \right) – \left( {5x – 9} \right)\left( {3x – 12} \right) = 0\) \( \Leftrightarrow \left( {5x – 9} \right)\left( {{x^2} – 5x + 4 – 3x + 12} \right) = 0\) \( \Leftrightarrow \left( {5x – 9} \right)\left( {{x^2} – 8x + 16} \right) = 0 \Leftrightarrow \left( {5x – 9} \right){\left( {x – 4} \right)^2} = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{5x – 9 = 0}\\{{{\left( {x – 4} \right)}^2} = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{5x = 9}\\{x – 4 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{9}{5}}\\{x = 4}\end{array}} \right.} \right.} \right.\) Vậy tập nghiệm của phương trình là : \(S = \left\{ {\frac{9}{5};4} \right\}\) |
0,25 điểm
0,25 điểm 0,25 điểm |
|
|
|
c) ĐKXĐ: \(x \ne 2,\,\,x \ne 4\) Với ĐKXĐ trên, phương trình đã cho trở thành \(x – 4 + 2\left( {x – 2} \right) = – \left( {x – 2} \right)\left( {x – 4} \right)\) \( \Leftrightarrow x – 4 + 2x – 4 = – {x^2} + 4x + 2x – 8\) \( \Leftrightarrow 3x – 8 = – {x^2} + 6x – 8 \Leftrightarrow 3x + {x^2} – 6x = 0\) \( \Leftrightarrow {x^2} – 3x = 0 \Leftrightarrow x\left( {x – 3} \right) = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x – 3 = 0}\end{array} \Leftrightarrow } \right.\left[ {\begin{array}{*{20}{c}}{x = 0(TM)}\\{x = 3(TM)}\end{array}} \right.\) Vậy tập nghiệm của phương trình là: \(S = \left\{ {0;3} \right\}\) |
0,25 điểm
0,25 điểm |
|
Câu 2 (2,0 điểm) |
a) \(8x – 1 > 5x – 7 \Leftrightarrow 8x – 5x > – 7 + 1 \Leftrightarrow 3x > 6 \Leftrightarrow x > 2\) Vậy tập nghiệm của bất phương trình là: \(S = \left\{ {x\left| {x > 2} \right.} \right\}\) Biểu diễn tập nghiệm trên trực số
|
0,25 điểm 0,25 điểm
0,25 điểm |
|
|
b) \(\frac{{x – 4}}{6} – \frac{{x – 1}}{3} \le 1 \Leftrightarrow x – 4 – 2\left( {x – 1} \right) \le 6\) \( \Leftrightarrow x – 4 – 2x + 2 \le 6 \Leftrightarrow – x – 2 \le 6 \Leftrightarrow – x \le 8 \Leftrightarrow x \ge – 8\) Vậy tập nghiệm của phương trình là: \(S = \left\{ {x\left| {x \ge – 8} \right.} \right\}\) Biểu diễn tập nghiệm trên trục số
|
0,5 điểm
0,25 điểm
|
|
|
c) \({\left( {x + 3} \right)^2} – {x^2} – 3x > 8 \Leftrightarrow {x^2} + 6x + 9 – {x^2} – 3x > 8\) \( \Leftrightarrow 3x + 9 > 8 \Leftrightarrow 3x > 8 – 9 \Leftrightarrow 3x > – 1 \Leftrightarrow x > \frac{{ – 1}}{3}\) Vậy tập nghiệm của phương trình là: \(S = \left\{ {x\left| {x > \frac{{ – 1}}{3}} \right.} \right\}\) Biểu diễn tập nghiệm trên trục số
|
0,25 điểm
0,25 điểm |
|
Câu 3 (2,0 điểm) |
Gọi chữ số hàng chục của số cần tìm là \(x\,\,\left( {x \in N*,\,x \le 9} \right)\) \( \Rightarrow \) chữ số hàng đơn vị của số cần tìm là \(11 – x\). Số cần tìm là \(10x + 11 – x = 9x + 11\) Đổi chỗ hai chữ số cho nhau, ta thu được số mới là \(10\left( {11 – x} \right) + x = 110 – 10x + x = 110 – 9x\) Theo đầu bài, ta có phương trình: \(\left( {110 – 9x} \right) – \left( {9x + 11} \right) = 27\) \( \Leftrightarrow 110 – 9x – 9x – 11 = 27 \Leftrightarrow 99 – 18x = 27\) \( \Leftrightarrow – 18x = 27 – 99 \Leftrightarrow – 18x = – 72 \Leftrightarrow x = 4\) (nhận) Chữ số hàng chục của số ban đầu là 4 Chữ số hàng đơn vị của số ban đầu là \(11 – 4 = 7\) Vậy số cần tìm là 47. |
0,25 điểm
0,5 điểm
0,5 điểm
0,25 điểm |
|
Câu 4 (3,0 điểm) |
– Vẽ hình đúng
|
0,5 điểm
|
|
a) Xét \(\Delta IAB\) có IL là đường phân giác (gt) \( \Rightarrow \frac{{LA}}{{LB}} = \frac{{IA}}{{IB}}\) Mà IB = IC ( AI là đường trung tuyến) Do đó : \(\frac{{LA}}{{LB}} = \frac{{IA}}{{IC}}\). |
0,5 điểm
0,25 điểm |
|
|
b) Xét \(\Delta CMN\) có \(AI//CM\) (gt) \( \Rightarrow \frac{{AI}}{{MC}} = \frac{{NA}}{{NC}}\) (hệ quả của định lí Ta-lét) \( \Rightarrow NA.MC = AI.NC\) |
0,5 điểm
0,25 điểm |
|
|
c) Xét \(\Delta ABC\) có \(LN//BC\) (gt) \( \Rightarrow \frac{{LA}}{{LB}} = \frac{{NA}}{{NC}}\) (định lí ta-lét) Ta có: \(\frac{{AI}}{{MC}} = \frac{{NA}}{{NC}} = \frac{{LA}}{{LB}} = \frac{{IA}}{{IC}} \Rightarrow MC = IC\) Vậy tam giác ICM cân tại C \( \Rightarrow \widehat {CIM} = \widehat {CMI}\) Mà \(\widehat {CMI} = \widehat {AIM}\) (so le trong và Cx // AI) Suy ra \(\widehat {CIM} = \widehat {AIM}\) Vậy IN là tia phân giác của góc AIC. |
0,25 điểm
0,25 điểm |
|
|
|
d) Ta có \(\widehat {ATI} = \widehat {BIT}\) (so le trong và \(AD//BC\)) Mà \(\widehat {AIT} = \widehat {BIT}\) (IT là phân giác \(\widehat {AIB}\)) Do đó \(\widehat {ATI} = \widehat {AIT} \Rightarrow \Delta ATI\) cân tại A \( \Rightarrow AT = AI\) Chứng minh tương tự, ta có \(AD = AI\). Do đó \(AT = AI = AD\) Vậy \(TD = 2AI\) |
0,25 điểm
0,25 điểm |
|
Câu 4 (0,5 điểm) |
Đổi 1 tấn = 1000kg Số tấn hàng hóa công ty cần vận chuyển là : \(450.7 + 300.4 = 4350\) (kg) Mà \(4350:1000 = 4\) (dư 350) Số xe chuyên dụng để vận chuyển hết lô hàng hóa đó cùng lúc ít nhất là 5 xe Thật vậy! Chúng ta có thể sắp xếp chở như sau: 3 xe mỗi xe chở 2 thùng hàng A, 1 xe chở 3 thùng hàng B, 1 xe chở 1 thùng hàng A và 1 thùng hàng B. |
0,25 điểm
0,25 điểm |
———————–
Chú ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa
Bộ 21 Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2022 – 2023 – Đề 9
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề 9)
I. Trắc nghiệm (2 điểm): Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1: Tập nghiệm của phương trình \[({x^2} + 25)\left( {{x^2} – \frac{9}{4}} \right) = 0\] là:
A. \[\left\{ { \pm \,5;\,\, \pm \frac{3}{2}} \right\}\];
B. \(\left\{ { – \,25;\,\,\frac{9}{4}} \right\}\);
C. \(\left\{ { \pm \,\frac{3}{2}} \right\}\);
D. \(\left\{ { – 5;\,\,\,\frac{3}{2}} \right\}\).
Câu 2: Nghiệm của bất phương trình: 12 – 3x ≤ 0 là:
A. x ≤ 4;
B. x ≥ 4;
C. x ≤ − 4;
D. x ≥ − 4.
Câu 3: Cho tam giác ABC đồng dạng với tam giác MNP và \(\frac{{{S_{ABC}}}}{{{S_{MNP}}}} = 9\).
A. \(\frac{{MN}}{{AB}} = 9\);
B. \(\frac{{MN}}{{AB}} = 3\);
C. \(\frac{{MN}}{{AB}} = \frac{1}{9}\);
D. \(\frac{{MN}}{{AB}} = \frac{1}{3}\).
Câu 4: Điền từ còn thiếu vào chỗ trống:
a) Nếu ba cạnh của tam giác này ……………. với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
b) Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó …………….. thì hai tam giác đó đồng dạng.
c) Nếu hai góc của tam giác này lần lượt ………………. của tam giác kia thì hai tam giác đó đồng dạng với nhau.
d) Tam giác vuông này có một góc nhọn bằng góc nhọn của ……… kia thì hai tam giác vuông đó đồng dạng.
II. Tự luận
Bài 1 (2,5 điểm): Giải các phương trình và bất phương trình sau:
a) 8x + 6 = 3x + 41;
b) \(\frac{{x + 2}}{{x – 2}} = \frac{1}{x} + \frac{2}{{x(x – 2)}}\);
c) \[\frac{{2x + 2}}{3} \ge 2 + \frac{{x – 2}}{2}\].
Bài 2 (1,5 điểm): Một người lái ô tô dự định đi từ A đến B với vận tốc 48 km/h. Nhưng sau khi đi được 1 giờ với vận tốc đó, ô tô bị tàu hỏa chắn đường trong 10 phút. Để kịp đến B đúng thời gian đã định, người đó phải tăng vận tốc thêm 6 km/h. Tính độ dài quãng đường AB.
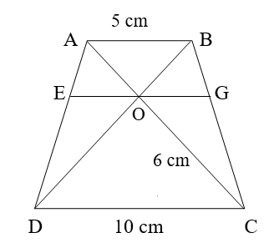
Bài 3 (3 điểm): Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD. Qua O kẻ đường thẳng song song với AB, cắt AD và BC theo thứ tự ở E và G.
a) Chứng minh: OA . OD = OB . OC.
b) Cho AB = 5 cm, CD = 10 cm và OC = 6 cm. Hãy tính OA, OE.
c) Chứng minh rằng: \(\frac{1}{{OE}} = \frac{1}{{OG}} = \frac{1}{{AB}} + \frac{1}{{CD}}\).
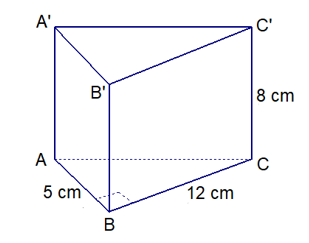
Bài 4 (1 điểm): Một hình lăng trụ đứng có đáy là tam giác vuông (như hình vẽ). Độ dài hai cạnh góc vuông của đáy là 5 cm, 12 cm, chiều cao của lăng trụ là 8cm. Tính diện tích xung quanh và thể tích của hình lăng trụ đó.
Đáp án
I. Trắc nghiệm (2 điểm):
Câu 1: Tập nghiệm của phương trình \[({x^2} + 25)\left( {{x^2} – \frac{9}{4}} \right) = 0\] là:
A. \[\left\{ { \pm \,5;\,\, \pm \frac{3}{2}} \right\}\];
B. \(\left\{ { – \,25;\,\,\frac{9}{4}} \right\}\);
C. \(\left\{ { \pm \,\frac{3}{2}} \right\}\);
D. \(\left\{ { – 5;\,\,\,\frac{3}{2}} \right\}\).
Giải thích:
Ta có: \[({x^2} + 25)\left( {{x^2} – \frac{9}{4}} \right) = 0\]
Û x2 + 25 = 0 hoặc \[{x^2} – \frac{9}{4} = 0\]
\[ \Leftrightarrow {x^2} = \frac{9}{4}\] (vì x2 + 25 > 0 \(\forall x \in \mathbb{R}\))
\[ \Leftrightarrow x = \pm \frac{3}{2}\].
Do đó, tập nghiệm của phương trình đã cho là \(S = \left\{ { \pm \,\frac{3}{2}} \right\}\).
Vậy chọn đáp án C.
Câu 2: Nghiệm của bất phương trình: 12 – 3x ≤ 0 là:
A. x ≤ 4;
B. x ≥ 4;
C. x ≤ − 4;
D. x ≥ − 4.
Giải thích:
Ta có: 12 – 3x ≤ 0
Û – 3x ≤ – 12
Û x ≥ 4.
Do đó, bất phương trình đã cho có nghiệm x ≥ 4.
Vậy chọn đáp án B.
Câu 3: Cho tam giác ABC đồng dạng với tam giác MNP và \(\frac{{{S_{ABC}}}}{{{S_{MNP}}}} = 9\).
A. \(\frac{{MN}}{{AB}} = 9\);
B. \(\frac{{MN}}{{AB}} = 3\);
C. \(\frac{{MN}}{{AB}} = \frac{1}{9}\);
D. \(\frac{{MN}}{{AB}} = \frac{1}{3}\).
Giải thích:
Do ∆ABC ∆MNP nên \(\frac{{{S_{ABC}}}}{{{S_{MNP}}}} = {\left( {\frac{{AB}}{{MN}}} \right)^2}\)
Mà \(\frac{{{S_{ABC}}}}{{{S_{MNP}}}} = 9 \Rightarrow \frac{{AB}}{{MN}} = 3\).
Do đó \(\frac{{MN}}{{AB}} = \frac{1}{3}\).
Vậy chon đáp án D.
Câu 4:
a) Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
b) Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
c) Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
d) Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
II. Tự luận
Bài 1 (2,5 điểm):
a) 8x + 6 = 3x + 41
8x − 3x = 41 − 6
5x = 35
x = 7.
Vậy tập nghiệm của phương trình đã cho là S = {7}.
b) \(\frac{{x + 2}}{{x – 2}} = \frac{1}{x} + \frac{2}{{x(x – 2)}}\)
ĐKXĐ: \(\left\{ \begin{array}{l}x \ne 0\\x – 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne 2\end{array} \right.\)
Phương trình đã cho tương đương:
\(\frac{{x(x + 2)}}{{x(x – 2)}} = \frac{{x – 2}}{{x(x – 2)}} + \frac{2}{{x(x – 2)}}\)
Suy ra: x(x + 2) = x – 2 + 2
x2 + 2x = x – 2 + 2
x2 + x = 0
x(x + 1) = 0
x = 0 hoặc x + 1 = 0
x = 0 (không TMĐK) hoặc x = −1 (TMĐK).
Vậy tập nghiệm của phương trình đã cho là S = {−1}.
c) \[\frac{{2x + 2}}{3} \ge 2 + \frac{{x – 2}}{2}\]
\[ \Leftrightarrow \frac{{2\,(2x + 2)}}{6} \ge \frac{{12}}{6} + \frac{{3\,(x – 2)}}{6}\]
2(2x + 2) ≥ 12 + 3(x – 2)
4x + 4 ≥ 12 + 3x – 6
4x + 4 ≥ 6 + 3x
4x – 3x ≥ 6 – 4
x ≥ 2.
Vậy tập nghiệm của bất phương trình là S = {x | x ³ 2}.
Bài 2 (1,5 điểm):
Gọi x (km) là độ dài quãng đường AB (ĐK: x > 48).
Thời gian dự định đi quãng đường AB là \[\frac{x}{{48}}\] (giờ).
Sau khi đi được 1 giờ, quãng đường còn lại ô tô phải đi là: x – 48 (km).
Thời gian đi trên quãng đường còn lại sau khi tăng vận tốc là: \[\frac{{x – 48}}{{54}}\] (giờ).
Vì thời gian dự định đi bằng tổng thời gian thực tế đi và thời gian chờ tàu nên ta có phương trình:
\[\frac{{x – 48}}{{54}} + 1 + \frac{1}{6} = \frac{x}{{48}}\]
\[ \Leftrightarrow \frac{{x – 48}}{{54}} + \frac{7}{6} = \frac{x}{{48}}\]
\[ \Leftrightarrow \frac{x}{{48}} – \frac{{x – 48}}{{54}} = \frac{7}{6}\]
\[ \Leftrightarrow \frac{{9x}}{{432}} – \frac{{8(x – 48)}}{{432}} = \frac{{504}}{{432}}\]
9x – 8(x – 48) = 504
9x – 8x + 384 = 504
x = 504 – 384
x = 120 (TMĐK).
Vậy độ dài quãng đường AB là 120 km.
Bài 3 (3 điểm):
a) Ta có AB // CD, áp dụng định lý Ta-let: \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}}\).
Do đó: OA . OD = OB . OC (đpcm).
b) Từ câu a suy ra: \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}}\)
\( \Leftrightarrow \frac{{OA}}{6} = \frac{5}{{10}} = \frac{1}{2}\)
\( \Leftrightarrow OA = \frac{6}{2} = 3\) (cm).
Do OE // DC nên theo hệ quả định lí Ta-let:
\(\frac{{AE}}{{AC}} = \frac{{AO}}{{AC}} = \frac{{EO}}{{DC}}\)
\( \Leftrightarrow \frac{3}{{3 + 6}} = \frac{{EO}}{{10}}\)
\( \Leftrightarrow EO = \frac{{3\,.\,\,10}}{9} = \frac{{10}}{3}\) (cm).
Vậy OA = 3 cm, \(EO = \frac{{10}}{3}\) cm.
c) Do OE // AB, theo hệ quả định lý Ta-lét ta có: \(\frac{{OE}}{{AB}} = \frac{{DE}}{{DA}}\) (1)
Do OE // CD, theo hệ quả định lý Ta-lét ta có: \(\frac{{OE}}{{DC}} = \frac{{AE}}{{DA}}\) (2)
Cộng vế theo vế của (1) và (2) ta được: \(\frac{{OE}}{{AB}} + \frac{{OE}}{{DC}} = \frac{{DE}}{{DA}} + \frac{{AE}}{{DA}} = 1\).
Suy ra \(OE\,\,\left( {\frac{1}{{AB}} + \frac{1}{{CD}}} \right) = 1\) hay \(\frac{1}{{OE}} = \frac{1}{{AB}} + \frac{1}{{CD}}\) (*)
Chứng minh tương tự, ta có: \(\frac{1}{{OG}} = \frac{1}{{AB}} + \frac{1}{{DC}}\) (**)
Từ (*) và (**) suy ra: \(\frac{1}{{OE}} = \frac{1}{{OG}} = \frac{1}{{AB}} + \frac{1}{{CD}}\) (đpcm).
Bài 4 (1 điểm):
Độ dài hai cạnh góc vuông của đáy là 5 cm, 12 cm nên ∆ABC vuông tại B.
Theo định lý Py-ta-go, ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{5^2} + {{12}^2}} = 13\) (cm).
Diện tích xung quanh của lăng trụ là:
(5 + 12 + 13) . 8 = 240 (cm2).
Diện tích một đáy của lăng trụ là:
\(\frac{1}{2}\,.\,\,5\,\,.\,\,12 = 30\) (cm2).
Thể tích của lăng trụ là:
30 . 8 = 240 (cm3).
Vậy hình lăng trụ có diện tích xung quanh là 240 cm2 và có thể tích là 240 cm3.
Bộ 21 Đề thi Toán lớp 8 Học kì 2 có đáp án năm 2022 – 2023 – Đề 10
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề 10)
Câu 1. (2,0 điểm) Giải các phương trình sau:
a) \( – {x^3} + 2{{\rm{x}}^2} + x – 2 = 0\) b) \(\frac{x}{{x – 1}} – \frac{{2\left( {x + 3} \right)}}{{x + 1}} = \frac{2}{{{x^2} – 1}}\)
c) \(2\left| {x + 1} \right| – 3{\rm{x}} = 5\)
Câu 2. (2,0 điểm) Giải bài toán sau bằng cách lập phương trình:
Hai thành phố A và B cách nhau 450km. Một ô tô đi từ A đến B với vận tốc không đổi trong một thời gian dự định. Khi đi, ô tô tăng vận tốc hơn dự kiến 5km/h nên đã đến B sớm hơn 1 giờ so với thời gian dự định. Tính vận tốc dự kiến ban đầu của ô tô?
Câu 3. (2,0 điểm) Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) \(3 + \frac{{x – 2}}{{ – 5}} < x – \frac{{x – 4}}{3} + \frac{{x + 3}}{2}\) b) \(\left( {x – 1} \right)\left( {{x^2} + 3{\rm{x}} + 1} \right) \ge \left( {x – 1} \right)\left( {x + 1} \right)\left( {x + 2} \right)\)
Câu 4. (3,5 điểm) Cho \(\Delta ABC\) nhọn, có các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh rằng: \(A{\rm{E}}.AC = {\rm{AF}}{\rm{.AB}}\)
b) Chứng minh rằng: \(\Delta AEF\) và \(\Delta ABC\) đồng dạng
c) Chứng minh rằng: EB là tia phân giác của \(\widehat {F{\rm{ED}}}\)
d) Gọi I là giao điểm của AD và EF. Chứng minh rằng: \(HI.AD = H{\rm{D}}.AI\)
Câu 5. (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức: \(A = {a^4} + 2{b^4} – a{b^3} – {a^3}b + 2015\) với a, b là các số thực.
———-HẾT———
Đáp án
|
Câu |
Đáp án và hướng dẫn chấm |
Biểu điểm |
|
Câu 1 (2,0 điểm) |
a) \( – {x^3} + 2{{\rm{x}}^2} + x – 2 = 0 \Leftrightarrow – {x^2}\left( {x – 2} \right) + \left( {x – 2} \right) = 0\) \( \Leftrightarrow \left( {x – 2} \right)\left( {1 – {x^2}} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x – 2 = 0\\1 – {x^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\{x^2} = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = \pm 1\end{array} \right.\) Vậy tập nghiệm của phương trình là \(S = \left\{ {2;1; – 1} \right\}\). |
0,25 điểm 0,25 điểm
0,25 điểm |
|
b) ĐKXĐ: \(x \ne 1,x \ne – 1\). Với ĐKXĐ trên phương trình trở thành \(x\left( {x + 1} \right) – 2\left( {x + 3} \right)\left( {x – 1} \right) = 2\) \( \Leftrightarrow {x^2} + x – 2{{\rm{x}}^2} + 2{\rm{x}} – 6{\rm{x}} + 6 = 2 \Leftrightarrow – {x^2} – 3{\rm{x}} + 4 = 0\) \( \Leftrightarrow – {x^2} + x – 4{\rm{x}} + 4 = 0 \Leftrightarrow \left( {x + 4} \right)\left( {1 – x} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x + 4 = 0\\1 – x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = – 4{\rm{ (nha\”a n)}}\\x = 1{\rm{ (loa\”i i)}}\end{array} \right.\) Vậy tập nghiệm của phương trình là \(S = \left\{ { – 4} \right\}\). |
0,25 điểm
0,25 điểm
0,25 điểm |
|
|
c) \(2\left| {x + 1} \right| – 3{\rm{x}} = 5\,(*)\) Nếu \(x \ge – 1\) thì \((*) \Leftrightarrow 2\left( {x + 1} \right) – 3{\rm{x}} = 5\) \( \Leftrightarrow 2{\rm{x}} + 2 – 3{\rm{x}} = 5 \Leftrightarrow – x + 2 = 5 \Leftrightarrow x = – 3\) (loại) Nếu \(x < – 1\) thì \((*) \Leftrightarrow – 2\left( {x + 1} \right) – 3x = 5\) \( \Leftrightarrow – 2{\rm{x}} – 2 – 3{\rm{x}} = 5 \Leftrightarrow – 5{\rm{x}} – 2 = 5 \Leftrightarrow x = – \frac{7}{5}\) (nhận) Vậy tập nghiệm của phương trình là \(S = \left\{ { – \frac{7}{5}} \right\}\). |
0,25 điểm
0,25 điểm |
|
|
Câu 2 (1,5 điểm) |
+) Gọi vận tốc ô tô dự định đi ban đầu là v (km/h) Thời gian ô tô đi từ A đến B với vận tốc v là: \[\frac{{450}}{v}\] (giờ) +) Khi đi, ô tô tăng vận tốc hơn dự kiến 5km/h nên thời gian ô tô đi hết quãng đường AB là: \[\frac{{450}}{{v + 5}}\] (giờ) +) Theo đề bài xe đến B sớm hơn 30 phút so với thời gian dự định nên ta có: \[\frac{{450}}{{v + 5}} + \frac{{60}}{{60}} = \frac{{450}}{v} \Leftrightarrow \frac{{450 + v + 5}}{{v + 5}} = \frac{{450}}{v}\] \[ \Leftrightarrow \left( {v + 455} \right).v = 450\left( {v + 5} \right)\] \[ \Leftrightarrow {v^2} + 455v – 450v – 2250 = 0\] \[ \Leftrightarrow {v^2} + 5v – 2250 = 0\] \[ \Leftrightarrow {v^2} – 45v + 50v – 2250 = 0\] \[ \Leftrightarrow v\left( {v – 45} \right) + 50\left( {v – 45} \right) = 0\] \[ \Leftrightarrow \left( {v + 50} \right)\left( {v – 45} \right) = 0\] \[ \Leftrightarrow \left[ \begin{array}{l}v + 50 = 0\\v – 45 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}v = – 50\\v = 45\end{array} \right.\begin{array}{*{20}{c}}{(ktm)}\\{(tm)}\end{array}\] Vậy vận tốc dự kiến ban đầu của ô tô là 45km/h. |
0,25 điểm
0,25 điểm
0,25 điểm
0,5 điểm
0,25 điểm |
|
Câu 3 (2,0 điểm) |
a) \(3 + \frac{{x – 2}}{{ – 5}} < x – \frac{{x – 4}}{3} + \frac{{x + 3}}{2}\) \( \Leftrightarrow 90 – 6\left( {x – 2} \right) < 30{\rm{x}} – 10\left( {x – 4} \right) + 15\left( {x + 3} \right)\) \( \Leftrightarrow 90 – 6{\rm{x}} + 12 < 30{\rm{x}} – 10{\rm{x}} + 40 + 15{\rm{x}} + 4\) \( \Leftrightarrow – 6{\rm{x}} + 102 < 35{\rm{x}} + 85 \Leftrightarrow – 6{\rm{x}} – 35{\rm{x}} < 85 – 102\) \( \Leftrightarrow – 41{\rm{x}} < – 17 \Leftrightarrow x > \frac{{17}}{{41}}\) Tập nghiệm của bất phương trình là \(S = \left\{ {x|x > \frac{1}{4}} \right\}\). Biểu diễn tập nghiệm trên trục số
|
0,5 điểm
0,25 điểm
0,25 điểm
|
|
|
b) \(\left( {x – 1} \right)\left( {{x^2} + 3{\rm{x}} + 1} \right) \ge \left( {x – 1} \right)\left( {x + 1} \right)\left( {x + 2} \right)\) \( \Leftrightarrow \left( {x – 1} \right)\left( {{x^2} + 3{\rm{x}} + 1} \right) – \left( {x – 1} \right)\left( {x + 1} \right)\left( {x + 2} \right) \ge 0\) \( \Leftrightarrow \left( {x – 1} \right)\left[ {\left( {{x^2} + 3{\rm{x}} + 1} \right) – \left( {x + 1} \right)\left( {x + 2} \right)} \right] \ge 0\) \( \Leftrightarrow \left( {x – 1} \right)\left( {{x^2} + 3{\rm{x}} + 1 – {x^2} – 2{\rm{x}} – x – 2} \right) \ge 0\) \( \Leftrightarrow – \left( {x – 1} \right) \ge 0 \Leftrightarrow x – 1 \le 0 \Leftrightarrow x \le 1\) Tập nghiệm của bất phương trình là \(S = \left\{ {x|x \le 1} \right\}\). Biểu diễn tập nghiệm trên trục số
|
0,5 điểm
0,25 điểm
0,25 điểm |
|
|
|
|
|
Câu 4 (3,5 điểm) |
– Vẽ hình đúng
a) Xét \(\Delta A{\rm{E}}B\) và \(\Delta AFC\) có \(\widehat {E{\rm{A}}B}\) (chung), \(\widehat {A{\rm{E}}B} = \widehat {AFC}\left( { = 90^\circ } \right)\). Do đó (g.g) \( \Rightarrow \frac{{A{\rm{E}}}}{{AF}} = \frac{{AB}}{{AC}} \Rightarrow AE.AC = AF.AB\) |
0,25 điểm
0,5 điểm 0,25 điểm |
|
b) Xét \(\Delta AEF\) và \(\Delta ABC\) có: \(\widehat {EAF}\) (chung), \(\frac{{A{\rm{E}}}}{{AB}} = \frac{{AF}}{{AC}}\) (cmt) Do đó (c.g.c) |
0,5 điểm
0,5 điểm |
|
|
c) Ta có Chứng minh tương tự trên, ta có Ta có \(\widehat {AEF} + \widehat {BEF} = \widehat {CED} + \widehat {BED}\left( { = 90^\circ } \right)\). Suy ra \(\widehat {BEF} = \widehat {BED}\) Vậy EB là tia phân giác của góc \(\widehat {FED}\).
|
0,25 điểm
0,5 điểm
0,25 điểm |
|
|
|
d) Gọi Ex là tia đối của tia ED Ta có \(\widehat {xEA} = \widehat {CE{\rm{D}}}\) (đối đỉnh) Nên \(\widehat {{\rm{x}}E{\rm{A}}} = \widehat {AEF}\) Ta có EH, EA là các đường phân giác trong, ngoài đỉnh E của tam giác DEI Do đó \(\frac{{HI}}{{H{\rm{D}}}} = \frac{{AI}}{{A{\rm{D}}}}\) Vậy \(HI.A{\rm{D}} = H{\rm{D}}.AI\). |
0,25 điểm
0,25 điểm |
|
Câu 5 (0,5 điểm) |
\(A = {a^4} + 2{b^4} – a{b^3} – {a^3}b + 2015\) \( = {a^4} – a{b^3} – {a^3}b + {b^4} + {b^4} + 2015\) \( = a\left( {{a^3} – {b^3}} \right) – b\left( {{a^3} – {b^3}} \right) + {b^4} + 2015\) \( = \left( {{a^3} – {b^3}} \right)\left( {a – b} \right) + {b^4} + 2015\) \( = {\left( {a – b} \right)^2}\left( {{a^2} + ab + {b^2}} \right) + {b^4} + 2015\) \( = {\left( {a – b} \right)^2}\left[ {{{\left( {a + \frac{b}{2}} \right)}^2} + \frac{{3{b^2}}}{4}} \right] + {b^4} + 2015 \ge 2015\) \(A \ge 2015\). Dấu “=” xảy ra \( \Leftrightarrow a = b = 0\). Vậy giá trị nhỏ nhất của biểu thức A là 2015 \( \Leftrightarrow a = b = 0\). |
0,25 điểm
0,25 điểm |
———————–
Chú ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa