Khái niệm hai tam giác đồng dạng - Trang Học trực tuyến

Tài liệu Khái niệm hai tam giác đồng dạng gồm các nội dung sau:

I. Lý thuyết

– Tổng hợp kiến thức trọng tâm cần nhớ về hai tam giác đồng dạng

II. Bài tập tự luyện

– Gồm 13 bài tập vận dụng giúp học sinh tự rèn luyện cách giải các bài tập Khái niệm hai tam giác đồng dạng

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG

I. LÝ THUYẾT

Định nghĩa: ΔA₁B₁C₁ gọi là đồng dạng với ∆ABC nếu:

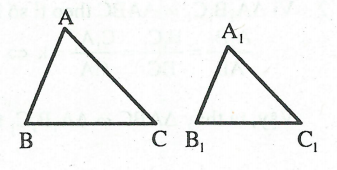
$\Rightarrow \{\begin{cases} \hat{A_{1}} = \hat{A,} \hat{B_{1}} = \hat{B}, \hat{C_{1}} = \hat{C} \\ \frac{A_{1} B_{1}}{A B} = \frac{B_{1} C_{1}}{B C} = \frac{C_{1} A_{1}}{C A} \end{cases} \begin{matrix} \end{matrix}$

Khi đó:

• Kí hiệu $△ A_{1} B_{1} C_{1} ~ △ A B C$

• Tỉ số $\frac{A_{1} B_{1}}{A B} = \frac{B_{1} C_{1}}{B C} = \frac{C_{1} A_{1}}{C A} = k$ gọi là tỉ số đồng dạng.

Chú ý: Khi viết $△ A_{1} B_{1} C_{1} ~ △ A B C$ , chúng ta cần hiểu ở đó có sự tương ứng giữa các đỉnh của hai tam giác với nhau, tức là không thể viết lại kí hiệu trên dưới dạng: $△ B_{1} A_{1} C_{1} ~ △ A B C$ ,

và nếu muốn đảo đỉnh thì cần đảo cả hai vế của dấu đồng dạng $△ B_{1} A_{1} C_{1} ~ △ A B C$

II. BÀI TẬP TỰ LUYỆN

Bài 1: Cho ∆ABC có AB = 3cm, BC = 4cm, CA = 5cm. Biết ∆A₁B₁C₁ đồng dạng với ΔABC.

a. Tính các cạnh A₁B₁, A₁C₁, biết B₁C₁= 8cm.

b. Tính các cạnh A₁B₁, B₁C₁, A₁C₁, biết $△ A_{1} B_{1} C_{1} ~ △ A B C$ theo tỉ số bằng 3.

Bài 2:

1. Nếu ∆ABC = ΔA₁B₁C₁ thì ΔA₁B₁C₁ có đồng dạng với ΔABC không? Tỉ số đồng dạng là bao nhiêu?

2. Nếu $△ A_{1} B_{1} C_{1} ~ △ A B C$ theo tỉ số k thì $△ A B C ~ △ A_{1} B_{1} C_{1}$ theo tỉ số nào?

Bâi 3: Cho hai tam giác ΔA₁B₁C₁ và ΔABC đồng dạng với nhau theo tỉ số k. Chứng minh rằng tỉ số chu vi của hai tam giác cũng bằng k.

Bài 4: Cho ΔABC. Kẻ đường thẳng a song song với cạnh BC và cắt hai cạnh AB, AC theo thứ tự tại M và N. Hai tam giác AMN và ABC có các góc và các cạnh tương ứng như thế nào?

Bài 5: Qua điểm O ở bên trong ΔABC kẻ các đường thẳng song song với các cạnh của tam giác. Các đường thẳng này chia tam giác thường 6 phần, trong đó có 3 tam giác lần lượt có diện tích là 4cm², 9cm², 16cm². Tính diện tích của ΔABC.

Bài 6: Trong hai mệnh đề sau đây, mệnh đề nào đúng? Mệnh đề nào sai?

a. Hai tam giác bằng nhau thì đồng dạng với nhau.

b. Hai tam giác đồng dạng với nhau thì bằng nhau.

Xem thêm

Bài liên quan:

Leave a Comment Hủy