Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
30 tính chất hình học Oxy điển hình
A- Chứng minh một số tính chất hình học
Tam giác – tứ giác – đường tròn.
Để giúp bạn đọc rèn luyện thêm cho mình nhũng kỹ năng trong quá trình chứng minh một số tính chất hình học, tác giả bổ sung thêm vào chuyên đề mục sau. Ngoài cách chứng minh đã nêu có thể có thêm những cách chứng minh khác nữa. Điều này tùy thuộc vào khả năng tư duy và lĩnh hội cũng như sở trường của mỗi người. Tựu trung lại thì hướng chứng minh vẫn xuất phát từ 4 con đường chính:
Một là, sử dụng “các tính chất hình học thuần túy của THCS”.
Hai là, sử dụng phương pháp “vécto thuần túy” (lớp 10).
Ba là, sử dụng phương pháp tọa độ hóa kết hợp “chuẩn hóa số liệu”.
Bốn là, sử dụng phương pháp tổng hợp (kết hợp các cách trên).
Tính chất 1: Cho tam giác ABC$vuông tại A, vẽ \(AH \bot BC\) tại H. Đường tròn ( C, AC) cắt đoạn thẳng BH tai D. CMR: AD là tia phân giác của góc BAH.
Hình vẽ
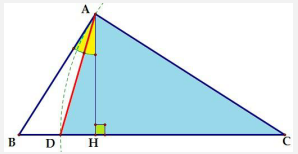
AD là phân giác góc BHA
Hướng dẫn chứng minh
Do CA = CD cân tại C.
Mặt khác, ta lại có:
\( \Rightarrow \)AD là phân giác góc BAH
Tính chất 2: Cho tam giác ABC vuông tại \(A(AB < AC)\). Gọi I là trung điểm cạnh AC. Qua I kẻ đường thẳng \({d_1}\) vuông góc với B , qua C kẻ đường thẳng \({d_2}\) vuông góc AC, \({d_1}\) cắt \({d_2}\) tại E . CM R : \(AE \bot BI\).
Hình vẽ
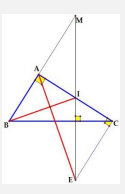
Hướng dẫn chứng minh:
Gọi \(M = IE \cap AB\).
Do \(\left\{ {\begin{array}{*{20}{l}}{CI \bot MB}\\{MI \bot BC}\end{array} \Rightarrow I} \right.\) là trực tâm của
Vi \( \Rightarrow IM = IE\)
Do đó AMCE là hình bình hành \( \Rightarrow AE//MC(2)\)
Từ \((1),(2) \Rightarrow BI \bot AE\)
Tính chất 3: Cho đường tròn (O;R) và AB là dây cung của đương tròn đó ( AB <2R, M là điềm thuộc cung lớn \(AB(M \ne A,M \ne B)\). Gọi H là hình chiểu vuông góc củn M trên AB. CMR: .
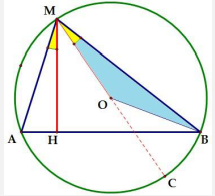
Kéo dài MO cắt ( O) tại điểm thứ 2 là đồng dạng
Hướng dẫn chứng minh:
Vẽ đường kính MC của đường tròn
Xét và có:
– (hai góc nội tiếp cùng chắn cung BM)
.
Tính chất 4: Cho tứ giác ABCD nội tiếp đường tròn (O), gọi M là giao điểm AB vì CD. Khi đó CMR: \(MB.MA = MCMD\)
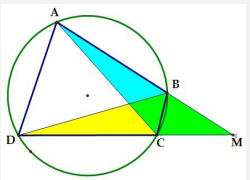
Hướng dần chứng minh:
Ta có ABCD là tứ giác nội tiếp
(hai góc nội tiếp cùng chắn cung
Xét và có
\( \Rightarrow \frac{{AM}}{{DM}} = \frac{{CM}}{{BM}} \Rightarrow AM \cdot BM = CM \cdot DM(dpcm)\)
Tính chất 5: Cho tứ giác ABCD, khi đó\(AC \bot BD \Leftrightarrow A{B^2} + C{D^2} = B{C^2} + A{D^2}\) (định lý 4 điểm).
Từ kết quả cuaqr tính chất trên, ta có thể sử dụng để chứng minh hai đường thẳng vuông góc.
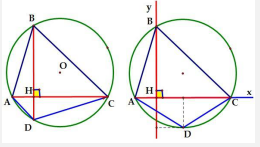
Hướng dẫn chứng minh:
Dựng hệ trục Hxy như hình vẽ.
Đặt \(A(a;0),C(c;0),B(0;b)\).
Giả sư: D(m,n)
Ta có
\(\begin{array}{l}A{B^2} = {a^2} + {b^2}\\C{D^2} = {c^2} – 2cm + {m^2} + {n^2}\\A{D^2} = {a^2} – 2am + {m^2} + {n^2}\\B{C^2} = {b^2} + {c^2}n\end{array}\)
Từ 4 đẳng thức trên ta có:
\(A{B^2} + C{D^2} = A{D^2} + B{C^2} \Rightarrow cm = am\)
Vi \(a \ne c \Rightarrow m = 0 \Rightarrow D(0;n) \in \) trục tung \( \Leftrightarrow AC \bot BD\)
Tính chất 6: Cho tam giác ABC ( AB < AC) có ba góc nhọn và hai đường cao BD, CE. Vē đường tròn tâm B bán kính BD cắt đoạn thẳng CE tại K, Qua D vẽ đường thẳng BC cắt đường thẳng BA tại M, cắt EC tại I. CMR:\(MK \bot BK\).
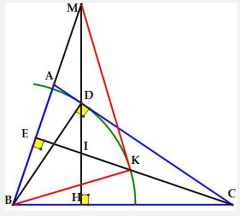
đồng dạng
Do đó ta cần chứng minh \(BE \cdot BM = B{K^2}\)
Hướng dẫn chứng minh:
Gọi \(H = DI \cap BC\). Ta có:
vuông tại D, DH là đường cao \( \Rightarrow BH.BC = B\)
Mà \(BD = BK = (R) \Rightarrow BE \cdot BM = B{K^2}\)
Tính chất 7: Cho tam giác ABC vuông tại A. Đường phân giác của góc ABC cắt đường trung trực của đọan thẳng AC ở D. CMR: vuông.
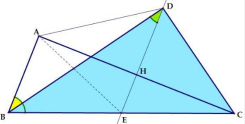
Ta sử dụng tính chất đường trung tuyến bằng nửa cạnh huyền thì là tam giác vuông.
Hướng dẫn chứng minh:
Gọi E là trung điểm B, do vuông tại \(A \Rightarrow \)EA = EC
Suy ra E thuộc đường trung trực cạnh \(AC \Rightarrow DE \bot AC\)
Mà \(AB \bot AC \Rightarrow AB//DE\)
cân tại \(D \Rightarrow ED = BE = \frac{{BC}}{2}\)
vuông tại D.
Tính chất 8: Cho điểm A ở ngoài đường tròn ( O). Vẽ cát tuyến ABC. ADE của đường tròn (O). Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD. CMR: Ax//DE.
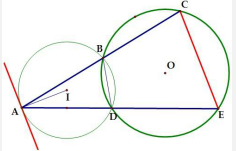
Để chứng minh song song, ta sử dụng tính chất so le trong của hai góc bằng nhau, đồng thời sử dụng các mối liên hệ của các góc trong đường tròn, tứ giác nội tiếp.
Hướng dẫn chứng minh:
Ta có
(góc giữa tiếp tuyến và dây cung và góc nội tiệp cùng chắn cung AB)
Mà
(do tứ giác BCED nội tiếp có góc ngoài bằng góc đối trong)
Tính chất 9: Cho tam giác ABC nhọn \((AB < AC)\), dựng về phía ngoài tam giác ABC các tam giác ABD vuông cân tại A, tam giác ACE vuông cân tại A. Gọi I là giao điểm BE và CD. Gọi M, N lần lượt là trung điểm của BC, DE. Chứng minh rằng \(AI//MN\).
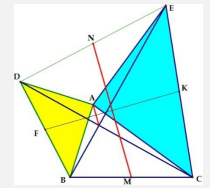
Gọi F, K lần lượt là trung điểm của BD, EC
Ta có :
Từ đó suy ra \[BE \bot CD\]
Dễ dàng chứng minh FNKM là hình thoi \[ \Rightarrow FK \bot MN\]
Ta có :
\[\left\{ {\begin{array}{*{20}{c}}{AF = IF = \frac{{AB}}{2}}\\{AK = IK = \frac{{EC}}{2}}\end{array}} \right.\]
Suy ra FK thuộc trung trực AI \[ \Rightarrow FK \bot AI\]
Do đó MN // AI
Tính chất 10: Cho tam giác ABC có H là trực tâm, d là đường phân giác trong góc HAC. Đường phân giác trong góc HBC cắt cạnh \(AD,{d_1},AC\) lần lượt tại M,N , I. CMR: \(AI \bot MN\).
Điều phải chứng minh
Để chứng minh hai góc trên bằng nhau ta có thể sử dụng kỹ thuật tách góc
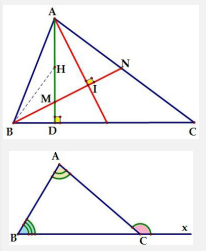
Hướng dẫn chứng minh:
Gọi \(D = AH \cap BC\) và \(E = BH \cap AC\)
Ta có
Lại có
cân tại A
Mà AI là đường phân giác MAN \( \Rightarrow AI \bot MN\)
Lưu ý:
Tính chất 11: Cho tam giác ABC vuông tại A đường cao AH, vẽ đường tròn tâm H bán kính HA. D là điểm trên đường (H). Gọi M, N lần lượt là trung điểm của DB, DC. C,R: DMHN là tứ giác nội tiếp.
Cần chứng minh là
Kéo dài HD cắt (H) để tạo đường kính và đồng thời khai thác các giả thiết của trung điểm
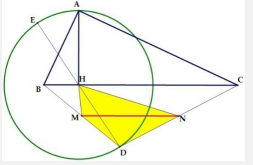
Hướng dẫn chứng minh
Gọi E là giao điểm của DH với đường tròn (H)
Ta có \(BH \cdot BC = A{H^2}( = DH.HE)\) (do vuông tại A )
\( \Rightarrow BH.BC = \) DH.HE
Lại có (đối đỉnh)
do \(MH//EB)\)
Tương tự ta có
Do đó tứ giác DMHN nội tiếp.
Tính chất 12: Cho hình vuông ABCD vẽ đường tròn (O) đường kính AB và đường tròn tâm D đường kính DC, Gọi E là giao điểm của hai đường tròn tren ( E khác A). Tia BE cắt CD tại M. CMR M là trung điểm của CD.
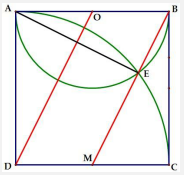
Cần chú ý đến tính chất hai đường tròn cắt nhau tại hai điểm A, E thì \(OD \bot AE\)
Hướng dẫn chứng minh
Ta có tam giác EAB vuông tại E
Do A, E là giao điểm của hai đường tròn \( \Rightarrow OD \bot AE\)
Mà \[BM \bot AE \Rightarrow OD//BM\], lại OB//DM có nên OBMD là hình bình hành
\[ \Rightarrow DM = OB = \frac{{CB}}{2}\]
\( \Rightarrow \)M là trung điểm của CD
Xem thêm