Chuyên đề phương pháp tọa độ trong mặt phẳng

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

Phương trình đường thẳng

Phương trình đường tròn

Phương trình đường elip

Chuyên đề phương pháp tọa độ trong mặt phẳng

Chương 3 Phương pháp tọa độ trong mặt phẳng

Bài 1. Phương trình đường thẳng

A) Tóm tắt lý thuyết

1. Vectơ pháp tuyến, vecơ chỉ phương

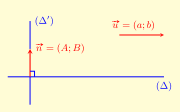
Chuyên đề phương pháp tọa độ trong mặt phẳng (ảnh 1)

– $\vec n = (A;B)$ là vectơ pháp tuyến của đường thẳng $(\Delta )$

$\left\{ {\begin{array}{*{20}{l}}{\vec n \in \left( {{\Delta ^\prime }} \right)}\\{\left( {{\Delta ^\prime }} \right) \bot (\Delta )}\end{array}} \right.$

\[\vec v = (a;b)\] là vectơ chỉ phương của đường thẳng $(\Delta )$

$\{\begin{cases} \vec{n} \in (Δ^{‘}) \\ (Δ^{‘}) ‖ (Δ) \end{cases}$

Chú ý

– Nếu $\vec n$, vecu theo thứ tự là vectơ pháp tuyến và vectơ chỉ phương của đường thẳng $(\Delta )$ thì $k.\vec n,m \cdot \vec u,(k,m \ne 0)$ cũng là pháp vectơ và vectơ chi phương của đường thẳng $(\Delta )$.

– Một đường thẳng hoàn toàn xác định khi biêt:

+ Hai diểm thuộc nó.

+ hoặc 1 điểm và biết phương của nó.

2) Phương trình đường thẳng

a) Phương trình tổng quát của đường thẳng

Mỗi đường thẳng trong mặt phẳng Oxy đều có phương trình

$Ax + By + C = 0,\left( {{A^2} + {B^2} > 0} \right)$

Ngược lại phương trình $Ax + By = C = 0,\left( {{A^2} + {B^2} > 0} \right)$ được gọi là phương trình tổng quát của đường thẳng.

Khi đó $\vec n = (A;B)$ được gọi vectơ pháp tuyến của đường thẳng.

b) Phương trình đường thẳng $(\Delta )$ qua một điểm $M\left( {{x_0};{y_0}} \right)$ có phương cho trước.

Phương của đường thẳng có thể được xác định bởi vectơ pháp tuyến, vectơ chi phưong, hệ số góc bằng k (hợp với chiều dương trục Ox một góc $\alpha $ có tan $\alpha = k$ )

– Phương trình tổng quát đường thẳng $(\Delta )$ qua một điểm và có vectơ pháp tuyến $\vec n = (A;B)$

\[A\left( {x – {x_0}} \right) + B\left( {y – {y_0}} \right) = 0\](1)

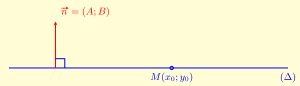
Chuyên đề phương pháp tọa độ trong mặt phẳng (ảnh 2)

Đặc biệt: $\vec n = (k; – 1)$ phương trình $(\Delta ):y = k\left( {x – {x_0}} \right) + {y_0}$ (Phương trình qua 1 diểm

và có hệ số k cho trước.)

– Phương trình tham số đường thẳng $(\Delta )$ qua một điểm và có vectơ chỉ phương $\vec u = (a;b)$

$\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + a.t}\\{y = {y_0} + b.t}\end{array},(t \in \mathbb{R})} \right.$(2 )

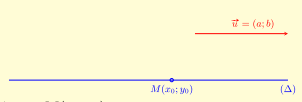
Chuyên đề phương pháp tọa độ trong mặt phẳng (ảnh 3)

Đường thẳng $(\Delta )$ có hệ số k và qua $M\left( {{x_0};{y_0}} \right)$

Đường thẳng $(\Delta )$ có vectơ chỉ phương $\vec u = (a;b)$ thì có số góc $k = \frac{b}{a}$ và

$(\Delta ):y = k\left( {x – {x_0}} \right) + {y_0}$( 2 ‘)

– Phương trình chính tắc đường thẳng $(\Delta )$ qua một điểm và có vectơ chỉ phương $\vec u = (a;b)$

$\frac{{x – {x_0}}}{a} = \frac{{y – {y_0}}}{b}$, với $a \ne 0,b \ne 0$(3)

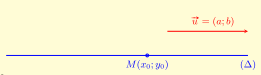
Chuyên đề phương pháp tọa độ trong mặt phẳng (ảnh 4)

a) Phương trình đường thẳng qua hai điểm $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)$

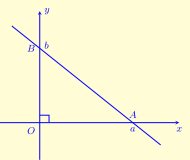
Chuyên đề phương pháp tọa độ trong mặt phẳng (ảnh 5)

$ \bullet \frac{{x – {x_A}}}{{{x_B} – {x_A}}} = \frac{{y – {y_A}}}{{{y_B} – {y_A}}}$ nếu $\left( {{x_B} \ne {x_A},{y_B} \ne {y_A}} \right.$(4)

– Nếu ${x_A} = {x_B}$ thì $\left[ {\begin{array}{*{20}{l}}{x = {x_A}}\\{x = {x_B}}\end{array}} \right.$ (4.1)

– Nếu ${y_A} = {y_B}$ thì $\left[ {\begin{array}{*{20}{l}}{y = {y_A}}\\{y = {y_B}}\end{array}} \right.$(4.2)

Phương trình theo đoạn chắn $A(a;0),B(0;b)$

– $\frac{x}{a} + \frac{y}{b} = 1$(5)

b) Chùm đường thẳng

Định nghĩa 1. Tập hợp các đường thẳng cùng đi qua một điểm I được gọi là chùm đường thẳng và I gọi là tâm của chùm.

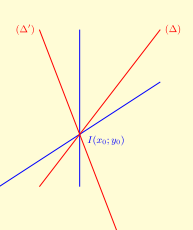
Chuyên đề phương pháp tọa độ trong mặt phẳng (ảnh 6)

Phương trình chùm đường thẳng có tâm $I\left( {{x_0};{y_0}} \right)$

– $\lambda \left( {x – {x_0}} \right) + \mu \left( {y – {y_0}} \right),\left( {{\lambda ^2} + {\mu ^2} > 0} \right)$

– $\lambda (Ax + By + C) + \mu \left( {{A^\prime }x + {B^\prime }y + {C^\prime }} \right) = 0,\left( {{\lambda ^2} + {\mu ^2} > 0} \right)$

với $I = (\Delta ) \cap \left( {{\Delta ^\prime }} \right)$

Trong đó $(\Delta ):Ax + By + C = 0,\left( {{\Delta ^\prime }} \right):{A^\prime }x + {B^\prime }y + {C^\prime } = 0,\left( {A:{A^\prime } \ne B:{B^\prime }} \right)$ và hai đường thẳng $(\Delta ),\left( {{\Delta ^\prime }} \right)$ được gọi là hai đường thẳng cơ sở của chùm.

3. Góc giữa đường hai thẳng

Gọi $\alpha $ là góc giữa hai đường thẳng $(\Delta )$ và $\left( {{\Delta ^\prime }} \right)$

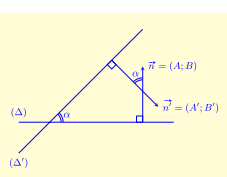
Chuyên đề phương pháp tọa độ trong mặt phẳng (ảnh 7)

– Nếu $(\Delta ):Ax + By + C = 0,\left( {{\Delta ^\prime }} \right):{A^\prime }x + {B^\prime }y + {C^\prime } = 0$

với $\left( {{A^2} + {B^2} > 0,{A^{\prime 2}} + {B^{\prime 2}} > 0} \right)$ thì ta có

$\cos \alpha = \frac{{\left| {A \cdot {A^\prime } + B \cdot {B^\prime }} \right|}}{{\sqrt {{A^2} + {B^2}} \cdot \sqrt {{A^{\prime 2}} + {B^{\prime 2}}} }}$

Đặc biệt: $(\Delta ) \bot \left( {{\Delta ^\prime }} \right) \Leftrightarrow A \cdot {A^\prime } + B \cdot {B^\prime } = 0$(6)

– Nếu $(\Delta ):y = ax + b$ và $\left( {{\Delta ^\prime }} \right):y = {a^\prime }x + {b^\prime }$ và

– Nếu $a.{a^\prime } \ne – 1$ thì $\tan \alpha = \left| {\frac{{a – {a^\prime }}}{{1 + a.{a^\prime }}}} \right|$

– Nếu $a \cdot {a^\prime } = – 1$ thì $(\Delta ) \bot \left( {{\Delta ^\prime }} \right)$(7)

(1) Chú ý

Từ (6) $\left( {{\Delta ^\prime }} \right) \bot (\Delta ):Ax + By + C = 0$

suy ra $\left( {{\Delta ^\prime }} \right):Bx – Ay + m = 0$.

Từ (7) $\left( {{\Delta ^\prime }} \right) \bot (\Delta ):y = ax + b$

suy ra $\left( {{\Delta ^\prime }} \right):y = – \frac{1}{a}x + {m^\prime }$.

4) Khoảng cách từ điểm $M\left( {{x_0};{y_0}} \right)$ đến đường thẳng $(\Delta ):Ax + By + C = 0$

Khoảng cách từ $M\left( {{x_0};{y_0}} \right)$ đến đường thẳng $(\Delta ):Ax + By + C = 0$ được cho bởi công thức

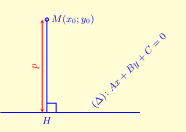
Chuyên đề phương pháp tọa độ trong mặt phẳng (ảnh 8)

$d = MH = \frac{{\left| {A \cdot {x_0} + B \cdot {y_0} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

5) Công thức đường phân giác

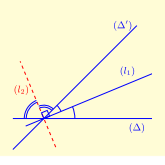
Chuyên đề phương pháp tọa độ trong mặt phẳng (ảnh 9)

Cho $(\Delta ):Ax + By + C = 0,\left( {{\Delta ^\prime }} \right):{A^\prime }x + {B^\prime }y + {C^\prime } = 0$. Các đường phân giác của $(\Delta )$ và $\left( {{\Delta ^\prime }} \right)$ được cho bởi công thức

$\frac{{Ax + By + C}}{{{A^2} + {B^2}}} = \pm \frac{{{A^\prime }x + {B^\prime }y + {C^\prime }}}{{{A^{\prime 2}} + {B^{\prime 2}}}}$

6)Vị trí tương đối của hai đường thả̛ng

Cho hai đường thẳng

$(\Delta ):Ax + By + C = 0,(\Delta ):{A^\prime }x + {B^\prime }y + {C^\prime } = 0$

Kí hiệu

$\begin{array}{l}D = \left| {\begin{array}{*{20}{c}}A&B\\{{A^\prime }}&{{B^\prime }}\end{array}} \right| = A \cdot {B^\prime } – {A^\prime }B;\\{D_x} = \left| {\begin{array}{*{20}{c}}B&C\\{{B^\prime }}&{{C^\prime }}\end{array}} \right| = B \cdot {C^\prime } – {B^\prime }C;\\{D_y} = \left| {\begin{array}{*{20}{l}}C&A\\{{C^\prime }}&{{A^\prime }}\end{array}} \right| = C \cdot {A^\prime } – {C^\prime }A\end{array}$

1) $(\Delta )$ và $\left( {{\Delta ^\prime }} \right)$ cắt nhau: $D \ne 0 \Leftrightarrow \frac{{{A^\prime }}}{A} \ne \frac{B}{{{B^\prime }}}$ khi đó tọa giao điểm $I:\left\{ {\begin{array}{*{20}{l}}{x = \frac{{{D_x}}}{D}}\\{y = \frac{{{D_y}}}{D}}\end{array}} \right.$

2) $(\Delta )$ và $\left( {{\Delta ^\prime }} \right)$ song song: $\frac{{{A^\prime }}}{A} = \frac{{{B^\prime }}}{B} \ne \frac{{{C^\prime }}}{{{C^\prime }}}$.

3) $(\Delta )$ và $\left( {{\Delta ^\prime }} \right)$ trùng nhau: $\frac{{{A^\prime }}}{A} = \frac{{{B^\prime }}}{B} = \frac{{{C^\prime }}}{C}$.

Hoặc xét hệ phương trình

$\left\{ {\begin{array}{*{20}{l}}{Ax + By + C = 0}\\{{A^\prime }x + {B^\prime }y + {C^\prime } = 0}\end{array}} \right.$(1)

– Nếu (I) có nghiệm thì $(\Delta )$ và $\left( {{\Delta ^\prime }} \right)$ cắt nhau.

– Nếu (I) vô nghiệm thì $(\Delta )$ và $\left( {{\Delta ^\prime }} \right)$ song song.

– Nếu (I) vô số nghiệm thì $(\Delta )$ và $\left( {{\Delta ^\prime }} \right)$ trùng nhau.

7) Vị trí tương đối của 2 điểm đối với đường thẳng

Cho hai điểm M, N và đường thẳng

$(\Delta ):f(x,y) = Ax + By + C = 0$

(1) Nếu $f(M) \cdot f(N) < 0$ thì M và N nằm khác phía đối với $(\Delta )$

(2) Nếu $f(M) \cdot f(N) > 0$ thì M và N nằm cùng phía đối với $(\Delta )$

B. Các dạng toán

Dạng 1. Viết phương trình đường thẳng qua 1 điểm và có phương

Kỹ thuật 1. Viết phương trình đường thẳng qua 2 điểm \[A\left( {{x_A}:{y_A}} \right),\quad B\left( {{x_B};{y_B}} \right)\]

Phương pháp:

(1) $(\Delta ):\left\{ {\begin{array}{*{20}{l}}{{\rm{ qua }}M\left( {{x_0};{y_0}} \right)}\\{VTPT\vec n = (A;B)}\end{array}} \right.$, phương trình tồng quát $(\Delta ):A\left( {x – {x_0}} \right) + B\left( {y – {y_0}} \right) = 0$

(2) $(\Delta ):\left\{ {\begin{array}{*{20}{l}}{qua\,M\left( {{x_0};{y_0}} \right)}\\{VTCP\,\vec u = (a;b)}\end{array}} \right.$, phương trình tham số $(\Delta ):\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + at}\\{y = {y_0} + b.t}\end{array},(t \in \mathbb{R})} \right.$.

(3) $(\Delta )$ : $\left\{ {\begin{array}{*{20}{l}}{{\rm{ qua }}M\left( {{x_0};{y_0}} \right)}\\{{\rm{ VTCP }}\vec u = (a;b)}\end{array}} \right.$, phương trinh chính tắc $(\Delta ):\frac{{x – {x_0}}}{a} = \frac{{y – {y_0}}}{b}$.

(4) $(\Delta )$ : $\left\{ {\begin{array}{*{20}{l}}{qua\,M\left( {{x_0};{y_0}} \right)}\\{{\rm{ he so goc }}k}\end{array}} \right.$, phương trình tổng quát $(\Delta ):y = k\left( {x – {x_0}} \right) + {y_0}$

(5) ( $\Delta )$ qua 2 điểm $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)$ có phương trình tổng quát: $\frac{{x – {x_A}}}{{{x_B} – {x_A}}} = \frac{{y – {y_A}}}{{{y_B} – {y_A}}}$.

(6) ( $\Delta $ ) qua 2 điểm $A(a;0),B(0;b)$ có phương trình đoạn chắn: $\frac{x}{a} + \frac{y}{b} = 1$.

(7)

$\begin{array}{l}\left( {{\Delta ^\prime }} \right) \bot (\Delta ):Ax + By + C = 0\\ \Rightarrow (\Delta ):Bx – Ay + m = 0\end{array}$

(8) $\left( {{\Delta ^\prime }} \right) \bot (\Delta ):y = ax + b \Rightarrow (\Delta ):y = – \frac{1}{a}x + {b^\prime }$

Ví dụ 1. Trong mặt phẳng Oxy, cho có $A(0;3),B( – 5;0),C( – 5; – 3)$.

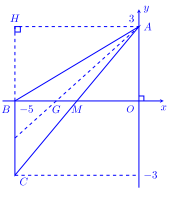
Chuyên đề phương pháp tọa độ trong mặt phẳng (ảnh 10)

1) Viết phương trình các cạnh , đường trung tuyến, đường cao AH

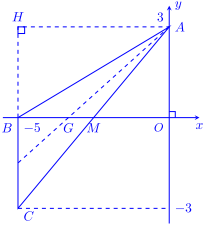
Chuyên đề phương pháp tọa độ trong mặt phẳng (ảnh 11)

– \[(AB):\frac{x}{{ – 5}} + \frac{y}{1} = 1 \Leftrightarrow 3x – 5y + 15 = 0\]

– Ta thấy \[{x_B} = {x_C} = – 5 \Rightarrow (BC):x = – 1\]

\[\begin{array}{l}(AC):\frac{{x – {x_C}}}{{{x_C} – {x_A}}} = \frac{{x – {x_C}}}{{{y_C} – {y_A}}}\\ \Leftrightarrow \frac{{x + 5}}{{0 + 5}} = \frac{{y + 3}}{{3 + 3}}\\ \Leftrightarrow 6(x + 5) = 5(y + 3)\\ \Leftrightarrow 6x – 5y + 15 = 0\end{array}\]

Phương trình trung tuyến BM

Gọi M là trung điểm của AC

$ \Rightarrow M:\left\{ {\begin{array}{*{20}{l}}{{x_M} = \frac{{{x_A} + {x_C}}}{2}}\\{{x_M} = \frac{{{y_A} + {y_C}}}{2}}\end{array} \Rightarrow \left\{ {{x_M} = – \frac{5}{2}\quad {y_M} = 0} \right.} \right.$ hay$M\left( { – \frac{5}{2};0} \right)$.

Thấy rằng ${y_M} = {y_B} = 0 \Rightarrow (BM):y = 0$.

2) Tính diện tích, xác định tọa độ trọng tâm

Gọi $H$ là chân đường cao từ $A$ của . Do suy ra $BC = \left| {{y_B} – {y_C}} \right| = 3$, $AH = \left| {{x_A} – {x_H}} \right| = 5$

– Diện tích là $S = \frac{1}{2}BC.AK = \frac{1}{2}3.5 = \frac{{15}}{2}$ (đvdt).

– Gọi $G$ là trọng tâm của , suy ra $G:\left\{ {\begin{array}{*{20}{l}}{{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}}\\{{x_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_G} = – \frac{{10}}{3}}\\{{y_G} = 0}\end{array}} \right.} \right.$

hay $G\left( { – \frac{{10}}{3};0} \right)$.

Kỹ thuật 2. Viết phương trình đường thẳng qua $M\left( {{x_0};{y_0}} \right)$ và có phương cho trước.

Ví dụ 2. Trong mặt phẳng Oxy, viết phương trình $(\Delta )$ đi qua $M(2; – 1)$ và thỏa:

a) có vecơ pháp tuyến là $\vec n = (1; – 3)$.

b) có vecơ chỉ phương là $\vec u = (4;6)$.

c) có hệ số góc $k = 3$.

Lời giải.

a) Đường thẳng $(\Delta )$ qua $M(2; – 1)$ có vecơ pháp tuyến $\vec n = (1; – 3)$ có phương trình tổng quát

$\begin{array}{l}{\rm{ 1}}{\rm{. }}(x – 2) – 3.(y + 1) = 0\\ \Leftrightarrow x – 2 – 3y – 3 = 0\\ \Leftrightarrow x – 3y – 5 = 0.{\rm{ }}\end{array}$

b) Đường thẳng $(\Delta )$ qua $M(2; – 1)$ có vecơ chỉ phương $\vec u = (4;6)$ hay $\overrightarrow {{u^\prime }} = (2;3)$ có phương trình tham số

$\left\{ {\begin{array}{*{20}{l}}{x = 2 + 2t}\\{y = – 1 + 3t}\end{array},(t \in \mathbb{R}).} \right.$

c) Đường thẳng $(\Delta )$ qua $M(2; – 1)$ có hệ số góc k = 3 có phương trình tổng quát

$\begin{array}{l}y = 3 \cdot (x – 2) – 1 \Leftrightarrow y = 3x – 6 – 1\\ \Leftrightarrow y = 3x – 7\end{array}$

Xem thêm

Bài liên quan:

Leave a Comment Hủy