Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
10 kỹ thuật tiếp cận để giải một bài toán hình học Oxy
Một số kỹ thuật điển hinh khi giải toán hình học tọa độ phắng
Bài 1: nội tiếp đường tròn đường kính \({\rm{AD}},{\rm{M}}(3; – 1)\) là trung điểm cạnh BC. Đường cao kẻ từ B của đi qua điểm \({\rm{E}}( – 1; – 3)\), điểm F(1;3) nằm trên đường thẳng AC. Tìm tọa độ đỉnh A và viết phương trình cạnh BC biết \({\rm{D}}(4; – 2)\)
Hướng dẫn tìm lời giải
+ Trước hết, khi gặp loại bài tập mà tam giác nội tiếp đường tròn, dữ kiện bài cho đường cao của tam giác thì ta thường nghĩ đến việc tạo ra 1 hình bình hành bằng cách:
– Nếu tam giác có 2 đường cao thì ta chỉ việc kẽ 1 đường kính đi qua đỉnh còn lại (không chứa 2 đường cao kia).
– Nếu tam giác có đường kính đi qua đỉnh và 1 đường cao thì ta sẽ kẻ đường cao thứ 2
(bài toán này ta sẽ làm nhu vậy)
+ Với bài toán này ta sẽ tạo ra điểm \({\rm{H}}\) là trực tâm ta chứng minh được BHCD là hình bình hành (cái này quá quen rồi phải không – tự làm nhé)
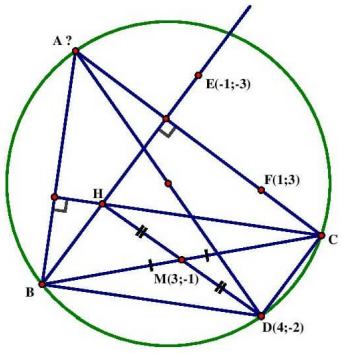
+ Công việc chuẩn bị đã xong, bây giờ ta sẽ làm theo các bước suy luận sau nhé:
– Thấy ngay H là trung điểm \({\rm{AC}} \Rightarrow {\rm{H}}(2;0)\)
– Lập được phương trình BH (qua 2 điểm H và E )
\( \Rightarrow {\rm{BH}}:{\rm{x}} – {\rm{y}} – 2 = 0\)
– Lập được phương trình DC (qua D và // BH )
\( \Rightarrow {\rm{DC}}:{\rm{x}} – {\rm{y}} – 6 = 0\)
– Lập được phương trình AC (qua F và \( \bot {\rm{BH}}\) )
\( \Rightarrow {\rm{AC}}\) : \({\rm{x}} + {\rm{y}} – 4 = 0\)
– Tọa độ \({\rm{C}} = {\rm{AC}} \cap {\rm{DC}}\), giải hệ \( \Rightarrow {\rm{C}}(5; – 1)\)
– Lập phương trình BC đi qua 2 điểm M và C
\[ \Rightarrow {\rm{BC}}:{\rm{y}} + 1 = 0\]
– Lập phương trình AH (qua H và \( \bot {\rm{BC}}\) )
\( \Rightarrow {\rm{AH}}:{\rm{x}} – 2 = 0\)
– Tọa độ \({\rm{A}} = {\rm{AH}} \cap {\rm{AC}}\), giải hệ \( \Rightarrow {\rm{A}}(2;2)\)
Bài 2: Cho nội tiếp đường tròn (C ) , đường phân giác trong và ngoài của \(\widehat {\rm{A}}\) cắt đường tròn (C ) lần lượt tại \({\rm{M}}(0; – 3),{\rm{N}}( – 2;1)\). Tìm tọa độ các điểm B,C biết đường thẳng BC đi qua \({\rm{E}}(2; – 1)\) và C có hoành độ dương.
Hướng dẫn tìm lời giải
+ Trước hết ta thấy ngay AN \( \bot {\rm{AM}}\) (t.c phân giác của 2 góc kề bù) \( \Rightarrow \) đường tròn (C) sẽ có tâm \({\rm{I}}( – 1; – 1)\) là trung điểm MN, bán kính \({\rm{R}} = \frac{{{\rm{MN}}}}{2} = \sqrt 5 \Rightarrow ({\rm{C}}):{({\rm{x}} + 1)^2} + {({\rm{y}} + 1)^2} = 5\)
+ Như vậy đến đây thấy rằng để tìm tọa độ \({\rm{B}},{\rm{C}}\) ta cần thiết lập phương trình đường thẳng BC rồi cho giao với đường tròn (C ).
Quan sát tiếp thấy BC qua \({\rm{E}}(2; – 1)\) rồi, giờ thì ta cần tìm VTCP hoặc VTPT nữa là ổn đúng không !
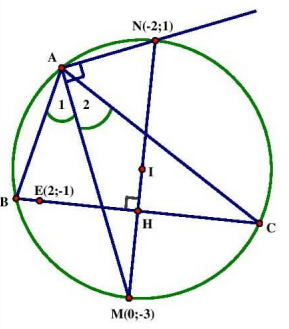
Nếu vẽ hình chính xác thì ta sẽ dự đoán được BC vuông góc MN ( ta sẽ chứng minh nhanh nhé)
\(\widehat {{{\rm{A}}_1}} = \widehat {{{\rm{A}}_2}} \Rightarrow \widehat {{\rm{MB}}} = \widehat {{\rm{MC}}} \Rightarrow M\)là điểm chính giũa là trung diểm BC\(({\rm{H}} = {\rm{MN}} \cap {\rm{BC}}) \Rightarrow {\rm{BC}} \bot {\rm{MN}}\) (quan hệ giữa đường kính và dây cung – hình học lớp 9))
+ Như vậy, tóm lại, đường thẳng BC qua \({\rm{E}}\), \( \bot {\rm{MN}}\)
\( \Rightarrow {\rm{BC}}:{\rm{x}} – 2{\rm{y}} – 4 = 0\)
+ Cuối cùng, ta chỉ cần giải hệ phương trình gồm \(({\rm{C}}) \cap {\rm{BC}}\)
\( \Rightarrow {\rm{B}}( – 2; – 3),{\rm{C}}\left( {\frac{6}{5}; – \frac{7}{5}} \right)\)
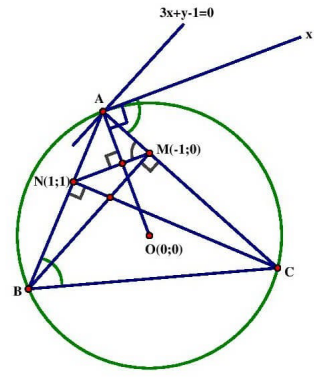
Bài 3: Cho nội tiếp đường tròn tâm O(0;0). Gọi \({\rm{M}}( – 1;0,\;{\rm{N}}(1;1)\) lần lượt là các chân đường vuông góc kẻ từ B,C của . Tìm tọa độ các đỉnh A,B,C của \(\Delta {\rm{ABC}}\), biết điểm A nằm trên đường thẳng \(\Delta \) có phương trình : \(3{\rm{x}} + {\rm{y}} – 1 = 0\)
Hướng dẫn tìm lời giải
Ta thấy \({\rm{A}} \in \Delta \Rightarrow {\rm{A}}({\rm{a}};1 – 3{\rm{a}})\), bây giờ cần thiết lập 1 phương trình để tìm a.
+ Vẽ hình chính xác chúng ta sẽ dự đoán được \({\rm{AO}} \bot {\rm{MN}}\) (Thật vậy: ta sẽ c.minh nhanh như sau: kẻ tiếp tuyến \(Ax \Rightarrow {\rm{Ax}} \bot {\rm{AO}}\) (*),
có , mà \(\widehat {{\rm{ABC}}} = \widehat {{\rm{AMN}}}\) ( do tứ giác MNBC nội tiếp)
\( \Rightarrow \widehat {{\rm{xAC}}} = \widehat {{\rm{AMN}}} \Rightarrow {\rm{Ax}}//{\rm{MN}}\) (**).
Từ (*) và \((**) \Rightarrow {\rm{AO}} \bot {\rm{MN}}\) )
Giải phương trình :
\(\overrightarrow {{\rm{AO}}} \cdot \overrightarrow {{\rm{MN}}} = 0 \Rightarrow {\rm{a}} = 1 \Rightarrow {\rm{A}}(1; – 2)\)
Đường thẳng AB đi qua A,N
\( \Rightarrow {\rm{AB}}:{\rm{x}} – 1 = 0\)
+ Đường thẳng AC đi qua A,M
\( \Rightarrow {\rm{AC}}:{\rm{x}} + {\rm{y}} + 1 = 0\)
+ Đường cao BM đi qua M và \( \bot {\rm{AC}} \Rightarrow {\rm{BM}}:{\rm{x}} – {\rm{y}} + 1 = 0\)
+ Tọa độ \({\rm{B}} = {\rm{AB}} \cap {\rm{BM}} \Rightarrow {\rm{B}}(1;2)\), tương tự \( \Rightarrow {\rm{C}}( – 2;1)\)
Như vậy điểm quan trọng nhất đối với bài này là phát hiện ra \({\rm{AO}} \bot {\rm{MN}}\)
Bây giờ ta cùng vận dụng PP trên làm bài tương tự sau nhé:
Bài 4 : Cho nội tiếp đường tròn tâm \(I(1;2)\), bán kính R = 5. Chân đường cao kẻ từ B, C lần lươt là \(H(3;3),K(0; – 1)\). Viết phương trình đường tròn ngoại tiếp tứ giác BCHK, biết A có tung độ duơng”
Hướng dẫn tìm lời giải
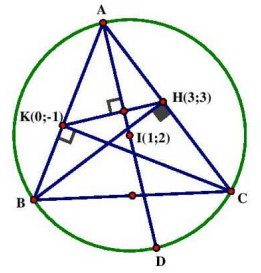
Đường tròn ( C) tâm I, bán kính R = 5 có phương trình \({(x – 1)^2} + {(y – 2)^2} = 25\)
+ Ta thấy ngay đường tròn ngoại tiếp tứ giác BCHK có tâm M là trung điểm BC, đường kính BC (do ). Như vậy vấn để quyết định của bài toán này là đi tìm tọa độ B,C.
+ Theo bài toán đã giới thiệu lần trước, do ta chứng minh được \({\rm{AI}} \bot {\rm{KH}} \Rightarrow {\rm{AI}}\) là đt qua \({\rm{I}},{\rm{AI}} \bot {\rm{KH}} \Rightarrow {\rm{AI}}\) có phương trình: \(3x + 4y – 11 = 0\)
+ Tọa độ \({\rm{A}} = {\rm{AI}} \cap ({\rm{C}})\), giải hệ có \({\rm{A}}( – 3;5)\)
+ Đường thẳng AB đi qua \({\rm{A}},{\rm{K}} \Rightarrow {\rm{AB}}:2{\rm{x}} + {\rm{y}} + 1 = 0\)
+ Tọa độ \({\rm{B}} = {\rm{AB}} \cap ({\rm{C}})\), giải hệ có \({\rm{B}}(1; – 3)\), suy luận tương tự có \({\rm{C}}(6;2)\)
Vậy đường tròn ngoại tiếp tứ giác \({\rm{BCHK}}\) có tâm \({\rm{M}}\) là trung điểm \({\rm{BC}}\), đường kính BC có phương trình: \({\left( {x – \frac{7}{2}} \right)^2} + {\left( {y + \frac{1}{2}} \right)^2} = \frac{{25}}{4}\)
Bài 5: (KD-2014) Cho nội tiếp đường tròn, D(1; -1) là chân đường phân giác của \(\widehat {\rm{A}},{\rm{AB}}\) có phương trình \(3{\rm{x}} + 2{\rm{y}} – 9 = 0\), tiếp tuyến tại A có phương trình \(\Delta :{\rm{x}} + 2{\rm{y}} – 7 = 0\). Hãy viết phương trình BC.
Hướng dẫn tìm lời giải
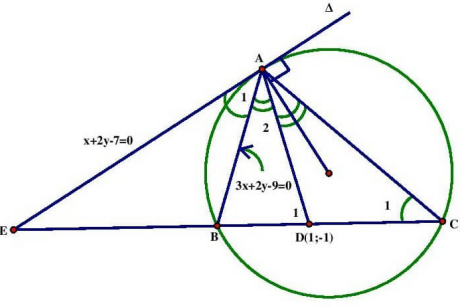
+ Với dữ kiện đề bài cho, trước hết ta xác định được ngay tọa độ
\({\rm{A}} = \Delta \cap {\rm{AB}} \Rightarrow {\rm{A}}(1;3)\)
+ Đường thẳng BC đi qua \(D(1; – 1)\) nên để lập phương trình BC ta cần tìm tọa độ một điểm nữa thuộc BC.
Gọi
\(E = \Delta \cap BC \Rightarrow E \in \Delta \Rightarrow E(7 – 2x;x)\)
+ Bây giờ cần thiết lập 1 phương trình để tìm x, vẽ hình chính xác sẽ cho ta dự đoán \(\Delta {\rm{EAD}}\) cân tại \({\rm{E}} \Rightarrow \) giải phương trình ED=EA sẽ tìm được \({\rm{x}} = 1 \Rightarrow {\rm{E}}(5;1)\).
(chứng minh \(\Delta {\rm{EAD}}\) cân tại E như sau: \(\widehat {{{\rm{D}}_1}} = \widehat {{{\rm{C}}_1}} + \widehat {{\rm{DAC}}}\) (góc ngoài \(\Delta {\rm{ADC}}\) ), mà \(\widehat {{{\rm{C}}_1}} = \widehat {{{\rm{A}}_1}} = \frac{{{\rm{sd}}\widehat {{\rm{AB}}}}}{2},\widehat {{\rm{DAC}}} = \widehat {{{\rm{A}}_2}} \Rightarrow \widehat {{{\rm{D}}_1}} = \widehat {{{\rm{A}}_1}} + \widehat {{{\rm{A}}_2}} = \widehat {{\rm{EAD}}} \Rightarrow \Delta {\rm{EAD}}\) cân tại E )
+ Đường thẳng BC đi qua 2 điểm E và \({\rm{D}} \Rightarrow {\rm{BC}}:{\rm{x}} – 2{\rm{y}} – 3 = 0\)
Bây giờ ta cùng vận dung PP trên làm bài tương tự sau nhé:
Bài 6 : “Cho có đỉnh S(1;5). Tâm đường tròn nội tiếp và ngoại tiếp \(\Delta {\rm{ABC}}\) lần lươt là \({\rm{I}}(2;2),{\rm{K}}\left( {\frac{5}{2};3} \right)\). Tìm tọa độ B, C.
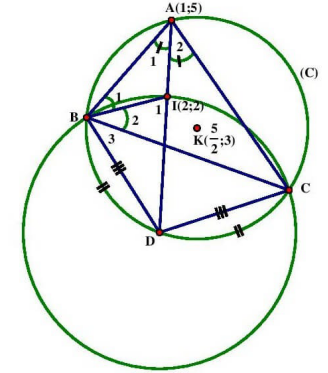
+ Ta lập được ngay đường tròn ( C) ngoại tiếp có tâm K, bán kính AK.
\( \Rightarrow ({\rm{C}}):{\left( {{\rm{x}} – \frac{5}{2}} \right)^2} + {({\rm{y}} – 3)^2} = \frac{{25}}{4}\)
+ Đường thẳng AI qua A, I
\( \Rightarrow {\rm{AI}}:3{\rm{x}} + {\rm{y}} – 8 = 0 \Rightarrow {\rm{D}} = {\rm{AI}} \cap ({\rm{C}}) \Rightarrow {\rm{D}}\left( {\frac{5}{2};\frac{1}{2}} \right)\)
+ Bây giờ ta cần chứng minh \({\rm{BD}} = {\rm{DI}} = {\rm{CD}} \Rightarrow {\rm{B}},{\rm{C}}\) nằm trên đường tròn (T) tâm D, bán kính DI \( \Rightarrow \) tọa độ B, C là giao của 2 đường tròn ( C) và (T )
(Thật vậy, bây giờ ta chứng minh ý (*) – đây là yếu tố quyết định của bài toán này !!!
– Ta có \(\widehat {{{\rm{A}}_1}} = \widehat {{{\rm{A}}_2}} \Rightarrow \widehat {{\rm{DB}}} = \widehat {{\rm{DC}}} \Rightarrow {\rm{DB}} = {\rm{DC}}\) (1)
– Mà \(\widehat {{{\rm{I}}_1}} = \widehat {{{\rm{A}}_1}} + \widehat {{{\rm{B}}_1}}\) (góc ngoài ), lại có
\(\widehat {{{\rm{A}}_1}} = \widehat {{{\rm{A}}_2}},\widehat {{{\rm{A}}_2}} = \widehat {{{\rm{B}}_3}} = \frac{{{\rm{sd}}\widehat {{\rm{DC}}}}}{2},\widehat {{{\rm{B}}_1}} = \widehat {{{\rm{B}}_2}}\)
\( \Rightarrow \widehat {{{\rm{I}}_1}} = \widehat {{{\rm{B}}_2}} + \widehat {{{\rm{B}}_3}} = \widehat {{\rm{IBD}}} \Rightarrow \Delta {\rm{BDI}}\) cân tại \(D \Rightarrow {\rm{DB}} = {\rm{DI}}(2)\)
– Từ \((1)\) và (2) \( \Rightarrow {\rm{BD}} = {\rm{DI}} = {\rm{CD}}(*)\) )
+ Như vậy đường tròn ( T) tâm D, bán kính DI có phương trình: \({\left( {{\rm{x}} – \frac{5}{2}} \right)^2} + {\left( {{\rm{y}} – \frac{1}{2}} \right)^2} = \frac{{10}}{4}\) \( + \{ B,C\} = (C) \cap (T) \Rightarrow \left[ {\begin{array}{*{20}{l}}{B(4;1),C(1;1)}\\{B(1;1),C(4;1)}\end{array}} \right.\)
Bài 7: Cho có tâm đường tròn bàng tiếp của góc A là \({\rm{K}}(2; – 9)\), đỉnh \({\rm{B}}( – 3; – 4),{\rm{A}}(2;6)\). Tìm tọa độ đỉnh C.
Hướng dẫn tìm lời giải
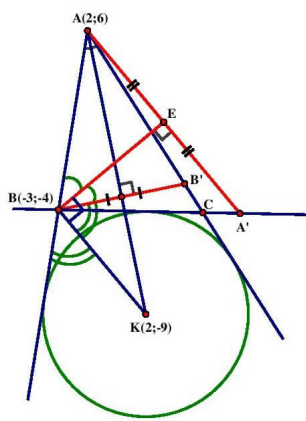
+ Ta thấy \({\rm{C}} = {\rm{AC}} \cap {\rm{BC}}\), vậy ta cần đi tìm phương trình đường thẳng AC và BC
* Bước 1: Tìm phương trình AC
– Đường thẳng AC đi qua \({\rm{A}}\) và \({\rm{B’}}\) (trong đó \({B^\prime }(7;4)\) là điểm đối xứng của B qua phân giác \(AK:x – 2 = 0\) )
\( \Rightarrow {\rm{AC}}:2{\rm{x}} + 5{\rm{y}} – 34 = 0\)
* Bước 2: Tìm phương trình BC
Suy luận tương tự ta cũng có: Đường thẳng BC đi qua B và \({{\rm{A}}^\prime }\) (trong đó \({{\rm{A}}^\prime }\) là điểm đối xứng của A qua phân giác BE )
+ Giải hệ \({\rm{C}} = {\rm{AC}} \cap {\rm{BC}}\).
Đáp số \({\rm{C}}(5;0)\)
Bài 8: nội tiếp đường tròn tâm \({\rm{I}}(2;1)\), bán kính \({\rm{R}} = 5\). Trực tâm \({\rm{H}}( – 1; – 1)\), độ dài \({\rm{BC}} = 8\). Hãy viết phương trình \({\rm{BC}}\).
Hướng dẫn tìm lời giài
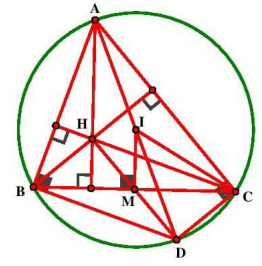
+ Đây là 1 bài toán quen thuộc “tam giác nội tiêp đường tròn, cho biết trực tâm”, vậy ta sẽ nghĩ ngay đến việc tạo ra hình bình hành bẳng cách kẻ đường kính \({\rm{AD}} \Rightarrow {\rm{BHCD}}\) là hình bình hành (bạn hãy tự xem lại cách chứng minh nhé) \( \Rightarrow {\rm{MI}}\) là đường trung bình của
\( \Rightarrow {\rm{AH}} = 2\).MI (một kết quả rất quen thuộc)
+ Với các suy luận trên, ta sẽ tìm được tọa độ A trước tiên.
Thật vậy, gọi A( x,y)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{\rm{AH}} = 2 \cdot {\rm{IM}} = 2 \cdot \sqrt {{\rm{C}}{{\rm{I}}^2} – {\rm{B}}{{\rm{M}}^2}} = 2\sqrt {{5^2} – {4^2}} = 6,}\\{{\rm{AI}} = 5}\end{array}} \right.\), giải hệ này
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{x}} = – 1}\\{{\rm{y}} = 5}\end{array} \Rightarrow {\rm{A}}( – 1;5) \Rightarrow {\rm{D}}(5; – 3) \Rightarrow {\rm{M}}(2; – 2)} \right.\)
(do I là trung điểm M là trung điểm HD )
+ Như vậy, sau khi có điểm A,M ta thấy đường thẳng BC đi qua M, vuông góc với \({\rm{AH}}\) \( \Rightarrow BC:y + 2 = 0\)
Xem thêm