Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Bài giảng chuyên đề Hình học Vecto giúp học sinh tự học
Chủ đề 2: Vecto – Tọa độ
Bài 1. Vecto
A – Tóm tắt lý thuyết
1. Khái niệm mở đầu:
* Vécto là một đoạn thẳng:
– Một đầu được xác định là gốc, còn đầu kia là ngon.
– Hướng tù gốc đến ngon gọ là hướng của vécto.
– Độ dài của vecto là độ dài đoạn thẳng xác định bởi điểm đầu và điểm cuối của véctơ.
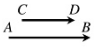
Ví dụ: Vecto \(\overrightarrow {AB} \)
![]()
– Điêm gốc: A
– Điểm ngọn: B
– Phurơng (giá): đường thẳng AB
– Hướng: từ A đến B
– Độ dài (môđun : độ dài đoạn AB
* Vecto có gốc A, ngọn B được kí hiệu là và độ dài của vecto \(\overrightarrow {AB} \) được kí hiệu là \(|\overrightarrow {AB} |\)là khoảng cách giữa điểm đầu và điểm cuối của véctơ. Ngoài ra, véctơ còn đuợc kí hiệu bởi một chũ cái in thường phía trên có mũi tên nhu \(\vec a,\vec b,\vec v,\vec u\) độ dài của \(\vec a\) kí hiệu: \(|\vec a|\).
* Vécto “không”, kí hiệu \(\vec 0\) là vécto có:
– Điểm gốc và điểm ngọn trùng nhau.
– Độ dài bằng 0 .
– Hướng bất kỳ
* Hai véctơ cùng phuơng khi chúng cùng nằm trên một đưòng thẳng hoạc nằm trên hai dưòng thẳng song song.
Hai cặp véctor \((\overrightarrow {AB} ,\overrightarrow {CD} )\) và \((\overrightarrow {MN} ,\overrightarrow {PQ} )\) đuợc goi là cùng phương.
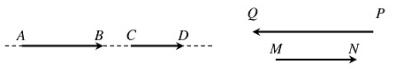
\(\overrightarrow {AB} \) cùng phurơng \(\overrightarrow {CD} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{AB//CD}\\{A,B,C,D{\rm{ thang hang }}}\end{array}} \right.\)
* Huớng của hai véctơ: Hai véctó cùng phưong có thể cùng hướng hoặc ngược hướng. Ta chi xét hướng của hai vécto khi chúng cùng phương.
– Hai véctor \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) gọi là cùng hướng:
\(\overrightarrow {AB} \uparrow \uparrow \overrightarrow {CD} \Leftrightarrow \left\{ \begin{array}{l}AB//CD\\{\rm{ Hai tia }}AB,CD{\rm{ cung huong }}\end{array} \right.\)
– Hai véctó \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) gọi là ngược hướng:
\(\overrightarrow {AB} \uparrow \uparrow \overrightarrow {CD} \Leftrightarrow \left\{ \begin{array}{l}AB//CD\\{\rm{ Hai tia }}AB,CD{\rm{ nguoc huong }}\end{array} \right.\)
![]()
* Góc của hai véctơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) là góc tạo bởi hai tia Ox, Oy lần lượt cùng hướng với hai tia AB và CD. Nghĩa là: \(\widehat {xOy} = (\widehat {AB,\overrightarrow {CD} })\).
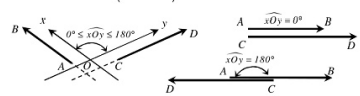
– Khi \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không cùng hướng thi
– Khi \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hứng thi
– Khi \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) nguợc huớng thì
* Hai véctơ bằng nhau khi và chỉ khi chúng cùng hướng và có độ dài bằng nhau.
\(\overrightarrow {AB} = \overrightarrow {CD} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\overrightarrow {AB} {\rm{ v\`a }}\overrightarrow {CD} {\rm{ c\`u ng huong }}}\\{|\overrightarrow {AB} | = |\overrightarrow {CD} |{\rm{ hay }}AB = CD}\end{array}} \right.\)

* Hai véctơ đối nhau khi và chỉ khi chúng ngự̣c hướng và có đọ̉ dài bằng nhau.
\(\overrightarrow {AB} = – \overrightarrow {CD} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\overrightarrow {AB} {\rm{ v\`a }}\overrightarrow {CD} {\rm{ nguoc huong }}}\\{|\overrightarrow {AB} | = |\overrightarrow {CD} |{\rm{ hay }}AB = CD}\end{array}} \right.\)
2. Các phép toán trên vectơ:
a) Tống của hai véctớ:
– Đinh nghĩa phép công 2 véctơ \(\vec a\) và \(\vec b\) là vécto \(\vec a + \vec b\), được xác định tùy theo vị trí của 2 vécto này. Có 3 trưòng họp:
(1) \(\vec a + \vec b\) nối đuôi
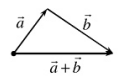
\(\vec a + \vec b\) được cộng theo quy tắc 3 điểm
(2) \(\vec a + \vec b\) cùng điểm gốc
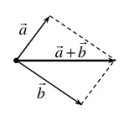
\(\vec a + \vec b\) được cộng theo quy tắc hình bình hành
(3) \(\vec a + \vec b\) là 2 vécto bất kỳ
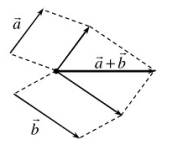
\(\vec a + \vec b\)được cộng theo hai trường hợp trên
* Qui tắc ba diểm: (Qui tắc tam giác hay qui tắc Chasles)
– Với ba điểm bất kỳ A,B,C ta có: \(\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {CB} \).
– Qui tắc 3 điểm còn được gọi là hệ thức Chasles dùng để công các vécto liên tiếp, có thể mở rộng cho truờng hợp nhiều vécto nhu sau:
\(\overrightarrow {{A_1}{A_n}} = \overrightarrow {{A_1}{A_2}} + \overrightarrow {{A_2}{A_3}} + \overrightarrow {{A_3}{A_4}} + \ldots + \overrightarrow {{A_{n – 1}}{A_n}} \)
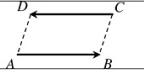
* Qui tắc hình bình hành:
Cho hình bình hành ABCD thì” \(\left[ {\begin{array}{*{20}{l}}{\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} }\\{\overrightarrow {DB} = \overrightarrow {DA} + \overrightarrow {DC} }\end{array}} \right.\) và \(\left[ {\begin{array}{*{20}{l}}{\overrightarrow {AB} = \overrightarrow {DC} }\\{\overrightarrow {AD} = \overrightarrow {BC} }\end{array}} \right.\)
– Qui tắc hình bình hành dùng để công các véctơ chung gốc.
Lưu ý: phép cộng véctơ không phải là phép công độ dài các véctơ.
– Tính chất:
+ Giao hoán: \(\vec a + \vec b = \vec b + \vec a\)
+ Kết hơp: \(\vec a + (\vec b + \vec c) = (\vec a + \vec b) + \vec c = (\vec a + \vec c) + \vec b\)
+ Cộng vói vécto đối: \(\vec a + ( – \vec a) = \vec 0\).
+ Cộng vóri vécto không: \(\vec a + \vec 0 = \vec 0 + \vec a = \vec a\).
b) Hiệu của hai véctơ:
* Vecto đối:
– Véctơ đối vécto \(\vec a\) kí hiện là \( – \vec a\).
– Tổng hai vecto đối là \(\vec 0:\vec a + ( – \vec a) = \vec 0\)
* Định nghĩa: hiệu hai véctơ \(\vec a\) và \(\vec b\) cho 2 kết quả \(\vec a – \vec b\) hoạc \(\vec b – \vec a\) đurợc xác định:
– \(\vec a – \vec b = \vec a + (\) véctó đối của \(\vec b) = \vec a + ( – \vec b)\)
– \(\vec b – \vec a = \vec b + (\) vécto đối của \(\vec a) = \vec b + ( – \vec a)\)
* Tính chất:
(1) \(\forall \vec a:\vec a – \vec a = \vec 0\)
(2) \(\forall \vec a:\vec a – \vec 0 = \vec a\)
(3) \( – \overrightarrow {AB} = \overrightarrow {BA} \)
* Qui tắc tam giác đối với hiện hai véctơ:
Với ba điểm bất kỳ A, B, C ta có: \(\overrightarrow {AB} = \overrightarrow {CB} – \overrightarrow {CA} \).
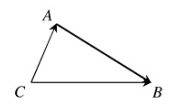
c) Tích của một số đối với một véctơ:
* Đinh nghĩa: Cho số thực \(k(k \ne 0)\) và một vecto \(\vec a(\vec a \ne \vec 0)\)
* Tính chất:
\(\begin{array}{l} – k(\vec a + \vec b) = k \cdot \vec a + k \cdot \vec b\quad \\ – (k + h) \cdot \vec a = k \cdot \vec a + h \cdot \vec a\quad \\ – k \cdot (h \cdot \vec a) = (k \cdot h) \cdot \vec a\end{array}\)
\(\begin{array}{l} – ( – 1)\vec a = – \vec a\\ – 1.\vec a = \vec a\end{array}\)
– \(0.\vec a = \vec 0\)
* Điều kiện để hai vecto cùng phương:
– Điều kiện cần và đủ để hai vécto \(\vec a;\vec b(\vec b \ne \vec 0)\) cùng phương là tồn tại một số \({\bf{k}}\) để \(\vec a = k \cdot \vec b.\)
– Hệ quả: Điều kiện cần và đủ để 3 điểm A, B, C thẳng hàng là \(\overrightarrow {AB} = k\overrightarrow {AC} \)
d) Trung điểm của đoạn thẳng và trọng tâm tam giác:
* Trung điểm của đoạn thẳng:
– I là trung điểm của AB :
\( \Leftrightarrow \overrightarrow {IA} + \overrightarrow {IB} = \vec 0\) hay \(\overrightarrow {AI} = \overrightarrow {IB} = \frac{1}{2}\overrightarrow {AB} \) hay \(\overrightarrow {IA} = – \overrightarrow {IB} \)
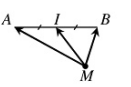
– I là trung điểm của AB, với M bất kì, ta có: \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \)
* Trọng tâm của tam giác:
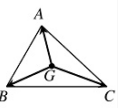
G là trọng tâm của
– Với M bất kì \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
B – Phương pháp giải toán
Vấn đề 1. Khái niệm vecto
I – Tóm tắt lý thuyết
– Vécto là 1 đoạn thẳng có hướng (có điểm đầu, điểu cuối)
– 1 đoạn thẳng AB xác định 2 véctơ: \(\overrightarrow {AB} ,\overrightarrow {BA} \).
– Véctơ dùng để giải các bài toán hình học và vật lý mà có tính chất “độ dài + hướng” (như các bài toán về chuyển động, lực, …)
– Độ dài vecto (modul) là độ dài đoạn thẳng tạo thành véctơ đó. Độ dài véctơ cũng là khoảng cách giữa hai điểm đầu mút. Kí hiệu: \(AB = |\overrightarrow {AB} | = |\overrightarrow {BA} |\).
– 2 vécto cùng phương khi giá của chúng song song hoặc cùng nằm trên đường thẳng.
– 2 vécto bằng nhau khi chúng cùng hướng và cùng độ dài.
– 2 vécto đối nhau khi chúng ngược hướng và cùng độ dài. Véctơ đối của \(\vec a\) là \( – \vec a\).
– Vécto không là véctơ có điểm gốc và điểm ngọn trùng nhau, độ dài là 0 , phương hướng tùy ý. Như vậy với mọi điểm A,B,C,… bất kỳ thì \(\overrightarrow {AA} = \overrightarrow {BB} = \overrightarrow {CC} = \ldots = \vec 0\).
II – Bài tập mẫu
Ví dụ 1. Cho hai điểm phân biệt A và B. Hỏi có bao nhiêu đoạn thẳng và bao nhiêu vectơ khác nhau và khác vectơ \(\vec 0\) ?
Ví dụ 2. Cho . Gọi P, Q và R là trung điểm các cạnh AB, BC và AC
a) Nêu các vecto có điểm đầu và điểm cuối là A, B và \(C\)
b) Nêu các vectơ bằng \(\overrightarrow {PQ} \)
b) Nêu các vectơ đối của \(\overrightarrow {PQ} \)
Ví dụ 3. Cho cân tại A. Gọi M là trung điểm của BC và N là trung điểm của A B.
a) Ta có: \(\overrightarrow {AB} = \overrightarrow {AC} \) đúng hay sai ?
b) Các vectơ nào cùng hướng với \(\overrightarrow {AC} \)
c) Các vectơ nào ngược hướng với \(\overrightarrow {BC} \) ?
d) Các vecto bằng nhau
Ví dụ 4. Cho hình bình hành ABCD có tâm là O. Dựa theo hình vẽ. Tìm:
a) Các vectơ bằng nhau \(( \ne \vec 0)\) có điểm đầu và điểm cuối trong 4 điểm A,B,C và D.
b) Các vectơ bằng nhau có điểm đầu và điểm cuối là O.
Ví dụ 5. Cho hình vuông ABCD tâm O. Nêu các vectơ \(( \ne \vec 0)\) bằng nhau mà có điểm đầu và điểm cuối trong các điểm A,B,C và D và O.
Ví dụ 6. Cho tứ giác ABCD. Gọi M,N,P,Q là trung điểm các cạnh AB, BC, CD,DA. Gọi O là giao điểm MP và QN. Chứng minh \(\overrightarrow {MO} = \overrightarrow {OP} \) và \(\overrightarrow {QO} = \overrightarrow {ON} \).
Ví dụ 7. Cho 4 điểm A,B,C,D. Chứng minh nếu \(\overrightarrow {AB} = \overrightarrow {DC} \) thì \(\overrightarrow {AD} = \overrightarrow {BC} \)
Xem thêm