Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu bao gồm các nội dung sau:
Các định nghĩa
Tổng, hiệu của hai vecto
Tích của vecto với một số
Trục tọa độ và hệ trục tọa độ
Chuyên đề vectơ có đáp án và lời giải chi tiết
Các định nghĩa
A – Lý thuyết tóm tắt
– Vectơ là một đoạn thẳng có hướng. Kí hiệu vectơ có điểm đầu A, điểm cuối B là \(\overrightarrow {AB} \).
– Giá của vectơ là đường thẳng chứa vectơ đó.
– Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ, kí hiệu \(|\overrightarrow {AB} |\).
– Vectơ – không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu \(\vec 0\).
– Hai vectơ đgl cùng phương nếu giá của chúng song song hoặc trùng nhau.
– Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng.
– Hai vectơ đgl bằng nhau nếu chúng cùng hướng và có cùng độ dài.
Chú ý:
+ Ta còn sủ dụng kí hiệu \(\vec a,\vec b, \ldots \) để biểu diễn vectơ:
+ Qui uớc: Vectơ \(\vec 0\) cùng phương, cùng hướng với mọi vectơ:
+ Mọi vectơ \(\vec 0\) đều bằng nhau.
B – Bài tập
I – Các ví dụ
Dạng 1: Xác một vectơ, sự cùng phương cùng hướng
Chú ý: với hai điểm phân biệt A, B ta có hai vectơ khác vectơ \(\vec 0\) là \(\overrightarrow {AB} ,\overrightarrow {BA} \)
Ví dụ 1: Cho 5 điểm A,B,C,D, E. Có bao nhiêu vectơ khác vectơ – không có điểm đầu và điểm cuối là các điểm đó.
Hướng dẫn giải:
Có 10 cặp điểm khác nhau
\(\{ {\rm{A}},{\rm{B}}\} ,\{ {\rm{A}},{\rm{C}}\} ,\{ {\rm{A}},{\rm{D}}\} ,\{ {\rm{A}},{\rm{E}}\} ,\{ {\rm{B}},{\rm{C}}\} ,\{ {\rm{B}},{\rm{D}}\} ,\{ {\rm{B}},{\rm{E}}\} ,\{ {\rm{C}},{\rm{D}}\} ,\{ {\rm{C}},{\rm{E}}\} ,\{ {\rm{D}},{\rm{E}}\} \). Do đó có 20 vectơ khác \(\vec 0\)
Ví dụ 2: Cho điểm A và vectơ \(\vec a\) khác \(\vec 0\). Tìm điểm M sao cho \(\overrightarrow {AM} \) cùng phương \(\vec a\)
Hướng dẫn giải:
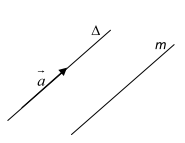
Gọi \(\Delta \) là giá của \(\vec a\)
Nếu \(\overrightarrow {AM} \) cùng phương \(\vec a\) thì đường thẳng \({\rm{AM}}//\Delta \)
Do đó M thuộc đường thẳng m đi qua \({\rm{A}}\) và \(//\Delta \)
Ngược lại, mọi điểm M thuôc m thì \(\overrightarrow {AM} \) cùng phương \(\vec a\)
Dạng 2: Chứng minh hai vectơ bằng nhau
Ta có thể dùng một trong các cách sau:
+ Sử dụng định nghĩa: \(\left. {\begin{array}{*{20}{c}}{|\vec a| = |\vec b|}\\{\vec a,\vec b{\rm{ c\`u ng hu?ng }}}\end{array}} \right\} \Rightarrow \vec a = \vec b\)
+ Sử dụng tính chất của các hình. Nếu ABCD là hình bình hành thì
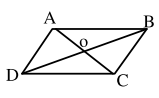
\(\overrightarrow {AB} = \overrightarrow {DC} ,\overrightarrow {BC} = \overrightarrow {AD} , \ldots \)
(hoặc viết ngược lại)
+ Nếu \(\vec a = \vec b,\vec b = \vec c \Rightarrow \vec a = \vec c\)
Ví dụ 3: Cho tam giác ABC có D, E, F lần lượt là trung điểm của BC, CA, AB. Chứng minh: \(\overrightarrow {EF} = \overrightarrow {CD} \)
Hướng dẫn giải:
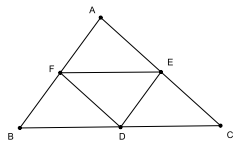
Cách 1: EF là đường trung bình của nên \({\rm{EF}}//{\rm{CD}}\),
\({\rm{EF}} = \frac{1}{2}{\rm{BC}} = {\rm{CD}} \Rightarrow {\rm{EF}} = {\rm{CD}} \Rightarrow |\overrightarrow {EF} | = |\overrightarrow {CD} |\)
\(\overrightarrow {EF} \) cùng hướng \(\overrightarrow {CD} \) (2)
Từ (1), (2) \( \Rightarrow \overrightarrow {EF} = \overrightarrow {CD} \)
Cách 2: Chứng minh EFDC là hình bình hành
\({\rm{EF}} = \frac{1}{2}{\rm{BC}} = {\rm{CD}}\) và \({\rm{EF}}//{\rm{CD}} \Rightarrow {\rm{EFDC}}\) là hình bình hành \( \Rightarrow \) \(\overrightarrow {EF} = \overrightarrow {CD} \)
Ví dụ 4: Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Điểm I là giao điểm của AM và BN, K là giao điểm của DM và C N.
Chứng minh: \(\overrightarrow {AM} = \overrightarrow {NC} ,\overrightarrow {DK} = \overrightarrow {NI} \)
Hướng dẫn giải:
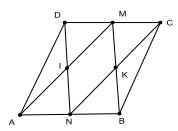
Ta có \({\rm{MC}}//{\rm{AN}}\) và \({\rm{MC}} = {\rm{AN}} \Rightarrow {\rm{MACN}}\) là hình bình hành \( \Rightarrow \overrightarrow {AM} = \overrightarrow {NC} \)
Tương tự MCDN là hình bình hành nên K là trung điểm của \({\rm{MD}} \Rightarrow \overrightarrow {DK} = \overrightarrow {KM} \). Tứ giác IMKN là hình bình hành, suy ra \(\overrightarrow {NI} = \overrightarrow {KM} \Rightarrow \overrightarrow {DK} = \overrightarrow {NI} \)
Ví dụ 5: Chứng minh rằng hai vectơ bằng nhau có chung điểm đầu (hoặc điểm cuối) thì chúng có chung điểm cuối (hoặc điểm đầu).
Hướng dẫn giải:
Giả sử \(\overrightarrow {AB} = \overrightarrow {AC} \). Khi đó AB= AC, ba điểm A,B,C thẳng hàng và B,C thuôc nửa đường thẳng góc \({\rm{A}} \Rightarrow {\rm{B}} \equiv {\rm{C}}\).
(trường hợp điểm cuối trùng nhau chứng minh tương tự)
Ví dụ 6: Cho điểm A và vectơ \(\vec a\). Dựng điểm M sao cho:
a) \(\overrightarrow {AM} = \vec a\);
b) \(\overrightarrow {AM} \) cùng phương \(\vec a\) và có độ dài bằng \(|\vec a|\).
Hướng dẫn giải:
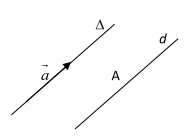
Giả sử \(\Delta \) là giá của \(\vec a\). Vẽ đường thẳng d đi qua A và \({\rm{d}}//\Delta \) (nếu A thuộc \(\Delta \) thì d trùng \(\Delta \) ). Khi đó có hai điểm \({{\rm{M}}_1}\) và \({{\rm{M}}_2}\) thuộc d sao cho: \({\rm{A}}{{\rm{M}}_1} = {\rm{A}}{{\rm{M}}_2} = |\vec a|\)
Khi đó ta có:
a) \(\overrightarrow {A{M_1}} = \vec a\)
b) \(\overrightarrow {A{M_1}} = \overrightarrow {A{M_2}} \) cùng phương với \(\vec a\)
II – Bài tập trắc nghiệm
Câu 1. Với hai điểm phân biệt A,B ta có được bao nhiêu vectơ có điểm đầu và điểm cuối là A hoặc B?
A. 2 .
B. 1 .
C. 3 .
D. 4 .
Hướng dẫn giải:
Chọn A.
đó là \(\overrightarrow {AB} ,\overrightarrow {BA} \).
Câu 2. Cho tam giác ABC. Có thể xác định bao nhiêu vectơ ( khác vectơ không ) có điềm đầu và điểm cuối là đỉnh A. B. C?
A. 2
B. 3
C. 4
D. 6
Hướng dẫn giải:
Chọn D.
Câu 3. Cho lục giác đều ABCDEF có tâm \({\rm{O}}\). Số các vectơ cùng hướng với vectơ \(\overrightarrow {{\rm{BC}}} \) có điểm đầu và điểm cuối là đỉnh của lục giác bằng bao nhiêu ?
A. 4 .
B. 3 .
C. 2 .
D. 6 .
Hướng dẫn giải:
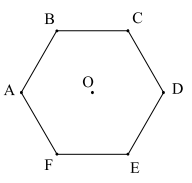
Chọn A
\(\mathop {{\rm{AO}}}\limits^ \to ,\overrightarrow {{\rm{OD}}} ,\overrightarrow {{\rm{AD}}} ,\overrightarrow {{\rm{FE}}} .\)
Câu 4. Cho tam giác ABC. Có thể xác định bao nhiêu vectơ (khác vectơ-không) mà có điểm đầu và điểm cuối là các đỉnh A,B,C ?
A. 6 .
B. 3 .
C. 2 .
D. 4 .
Hướng dẫn giải
Chọn A.
vì có 6 vectơ là : \(\overrightarrow {{\rm{AB}}} ,\overrightarrow {{\rm{BA}}} ,\overrightarrow {{\rm{AC}}} ,\overrightarrow {{\rm{CA}}} ,\overrightarrow {{\rm{BC}}} ,\overrightarrow {{\rm{CB}}} \).
Câu 5. Cho ngũ giác ABCD$. Có bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối là đỉnh của ngũ giác.
A. 10
B. 13
C. 14
D. 16
Chọn A.
Hai điểm phân biệt, chẳng hạn A, B ta xác định được hai vectơ khác vectơ-không là \(\overline {AB} ,\overline {BA} \). Mà từ năm đỉnh A, B, C, D, E của ngũ giác ta có 5 cặp điểm phân biệt do đó có 10 vectơ thỏa mãn yêu cầu bải toán.
Câu 6. Cho lục giác A B C D E F. Có bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối lả đỉnh của ngũ giác.
A. 20
B. 12
C. 14
D. 16
Hướng dẫn giải:
Chọn B.
Hai điểm phân biệt, chẳng hạn A, B ta xác định được hai vectơ khác vecto-không là \(\overrightarrow {AB} ,\overrightarrow {BA} \). Mà từ sáu dinh A, B, C, D, E, F của lục giác ta có 10 cặp diểm phân biệt do đó có 12 vectơ thỏa mãn yều cầu bải toán.
Câu 7. Cho tam giác ABC. Gọi M, N, lần lượt là trung diểm của BC, CA, AB. Có bao nhiêu vectơ khác vectơ – không củng phương với \(\overrightarrow {MN} \)có điểm đầu vả điểm cuối lấy trong điểm đã cho.
A. 5
B. 6
C. 7
D. 8
Hướng dẫn giải:
Chọn C.
Các vectơ khác vectơ không cùng phương với \(\overrightarrow {MN} \) là \(\overrightarrow {NM} ,\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {AP} ,\overrightarrow {PA} ,\overrightarrow {BP} ,\overrightarrow {PB} \).
Câu 8. Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB, Có bao nhiêu vectơ khác vectơ – không củng hướng với \(\overline {AB} \) có điềm đầu và điểm cuối lấy trong điểm đã cho.
A. 3
B. 4
C. 6
D. 5
Hướng dẫn giải:
Chọn A.
Các vecto khác vecto – không cùng hướng với \(\overrightarrow {AB} \) là \(\overrightarrow {AP} ,\overrightarrow {PB} ,\overrightarrow {NM} \).
Câu 9. Mệnh đề nào sau đây đúng ?
A. Có duy nhất một vectơ cùng phương với mọi vectơ
B. Có ít nhất hai vectơ cùng phương với mọi vectơ
C. Có vô số vectơ cùng phương với mọi vectơ
D. Không có vectơ nào cùng phương với mọi vectơ
Hướng dẫn giải:
Chọn A.
Câu 10. Khẳng định nào sau đây đúng ?
A. Hai vectơ \(\vec a\) và \(\vec b\) được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài.
B. Hai vectơ \(\vec a\) và \(\vec b\) được gọi là bằng nhau nếu chúng cùng phương và cùng độ dài.
C. Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) được gọi là bằng nhau khi và chỉ khi tứ giác ABCD là hình bình hành
D. Hai vectơ \(\vec a\) và \(\vec b\) được gọi là bằng nhau nếu cùng độ dài.
Hướng dẫn giải:
Chọn A.
Câu 11. Cho vectơ \(\vec a\), mệnh đề nào sau đây đúng ?
A. Có vô số vectơ \(\vec u\) mà \(\vec a = \vec u\)
B. Có duy nhất một vectơ \(\vec u\) mà \(\vec a = \vec u\)
C. Có duy nhất một vectơ \(\vec u\) mà \(\vec u = – \vec a\)
D. Không có vectơ \(\vec u\) nào mà \(\vec a = \vec u\)
Hướng dẫn giải:
Chọn A.
Câu 12. Cho hai vectơ không cùng phương \(\vec a\) và \(\vec b\). Khẳng định nào sau đây đúng :
A. Không có vectơ nào cùng phướng với cả hai vectơ \(\vec a\) và \(\vec b\)
B. Có vô số vectơ cùng phướng với cả hai vectơ \(\vec a\) và \(\vec b\)
C. Có một vectơ cùng phướng với cả hai vectơ \(\vec a\) và \(\vec b\), đó là \(\vec 0\)
D. Cả A, B, C đều sai.
Hướng dẫn giải:
Chọn C.
Câu 13. Chọn câu sai trong các câu sau. Vectơ có điểm đầu và điểm cuối trùng nhau được gọi là :
A. Được gọi là vectơ suy biến
B. Được gọi là vectơ có phương tùy ý
C. Được gọi là vectơ không, kí hiệu \(\vec 0\)
D. Là vectơ có độ dài không xác định.
Hướng dẫn giải:
Chọn D.
Câu 14. Chọn khẳng định đúng nhất trong các khẳng định sau:
A. Vectơ là một đoạn thẳng có định hướng.
B. Vectơ không là vectơ có điểm đầu và điểm cuối trùng nhau
C. Hai vectơ được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài
D. Cả A,B,C đều đúng.
Hướng dẫn giải:
Chọn D.
Câu 15. Mệnh đề nào sau đây đúng:
A. Hai vectơ cùng phương với một vectơ thứ ba khác \(\vec 0\) thì cùng hướng
B. Hai vectơ cùng phương với một vectơ thứ ba khác \(\vec 0\) thì cùng phương
C. Hai vectơ cùng phương với một vectơ thứ ba thì cùng phương
D. Hai vectơ ngược hướng với một vectơ thứ ba thì cùng hướng
Hướng dẫn giải:
Chọn B.
A Sai vì hai vectơ đó có thể ngược hướng.
B Đúng
C Sai vì thiếu điều kiện khác \(\vec 0\)
D Sai vì thiếu điều kiện khác \(\vec 0\)
Câu 16. Xét các mệnh đề :
(I) vectơ-không là vectơ có độ dài bằng 0
(II) vectơ-không là vectơ có nhiều phương.
Mệnh đề nào đúng ?
A. Chỉ (I) đúng
B. Chỉ (II) đúng
C. (I) và (II) đúng
D. (I) và (II) sai
Hướng dẫn giải:
Chọn C.
Câu 17. Khẳng định nào sau đây sai ?
A. Hai vectơ cùng phương với một vectơ thứ ba khác vectơ-không thì cùng phương với nhau
B. Hai vectơ cùng hướng với một vectơ thứ ba khác vectơ-không thì cùng hướng với nhau
C. Ba vectơ đều khác vectơ-không và đôi một cùng phương thì có ít nhất hai vectơ cùng hướng
D. Điều kiện cần và đủ để \(\vec a = \vec b\) là \(|\vec a| = |\vec b|\).
Hướng dẫn giải:
Chọn D.
Câu 18. Cho 3 điểm phân biệt A,B,C . Khi đó đẳng thức nào sau đây đúng nhất?
A. A,B,C thẳng hàng khi và chỉ khi \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương.
B. A,B,C thẳng hàng khi và chỉ khi \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) cùng phương.
\({\rm{C}}\). A,B,C thẳng hàng khi và chỉ khi \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \) cùng phương.
D. Cả A,B,C đều đúng.
Hướng dẫn giải:
Chọn D.
Câu 19. Cho 3 điểm A, B, C phân biệt. Khi đó;
A. Điều kiện cần và đủ để A.B.C thẳng hàng là \(\overrightarrow {AB} \) cùng phướng với \(\overrightarrow {AC} \)
B. Điều kiện đủ để A.B.C thẳng hàng là với mọi \({\rm{M}},\overrightarrow {MA} \) cùng phương với \(\overrightarrow {AB} \)
C. Điều kiện cần để A.B.C thẳng hàng là với mọi \({\rm{M}},\overrightarrow {MA} \) cùng phương với \(\overrightarrow {AB} \)
D. Điều kiện cần và đủ để A.B.C thẳng hàng là \(\overrightarrow {AB} = \overrightarrow {AC} \)
Hướng dẫn giải:
Chọn A.
Câu 20. Theo định nghĩa, hai vectơ được gọi là cùng phương nếu
A. giá của hai vectơ đó song song hoặc trùng nhau.
B. hai vectơ đó song song hoặc trùng nhau.
C. giá của hai vectơ đó song song.
D. giá của hai vectơ đó trùng nhau.
Hướng dẫn giải:
Chọn A.
Vì đúng theo định nghĩa hai vectơ cùng phương.
Xem thêm