Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Chuyên đề Vectơ – có lời giải chi tiết
Chuyên đề vectơ
Câu 785. [0H1-1] Véctơ có điểm đầu là A, điểm cuối là B được kí hiệu là
A. AB.
B. \(|\overrightarrow {AB} |\).
C. \(\overrightarrow {BA} \).
D. \(\overrightarrow {AB} \).
Lời giải
Chọn D.
Câu 786. [0H1-1] Trong mặt phẳng tọa độ Oxy, cho hai điểm A(-4;0) và B( 0;3). Xác định tọa độ của vectơ \(\vec u = 2\overrightarrow {AB} \).
A. \(\vec u = ( – 8; – 6)\).
B. \(\vec u = (8;6)\).
C. \(\vec u = ( – 4; – 3)\).
D. \(\vec u = (4;3)\).
Lời giải
Chọn \({\rm{B}}\).
\(\overrightarrow {AB} = (4;3) \Rightarrow \vec u = 2\overrightarrow {AB} = (8;6).\)
Câu 787. [0H1-1] Trong mặt phẳng tọa độ Oxy, cho \(A(3; – 1),B( – 1;2)\) và \(I(1; – 1)\). Tìm tọa độ điểm C để I là trọng tâm tam giác ABC.
A. \(C(1; – 4)\).
B. \(C(1;0)\).
C. \(C(1;4)\).
D. \(C(9; – 4)\).
Chọn A.
Lời giải
Điểm I là trọng tâm tam giác \(ABC \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_I} = \frac{{{x_A} + {x_B} + {x_C}}}{3}}\\{{y_I} = \frac{{{y_A} + {y_B} + {y_C}}}{3}}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_C} = 3{x_I} – {x_A} – {x_B}}\\{{y_C} = 3{y_I} – {y_A} – {y_B}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_C} = 3 – 3 – ( – 1) = 1}\\{{y_C} = – 3 – ( – 1) – 2 = – 4}\end{array}} \right.} \right.{\rm{. }}\)
Vậy điểm C(1;-4).
Câu 788. [0H1-1] Xét các mệnh đề sau
(I): Véc tơ – không là véc tơ có độ dài bằng 0 .
(II): Véc tơ – không là véc tơ có nhiều phương.
A. Chỉ (I) đúng.
B. Chỉ (II) đúng.
C. (I) và (II) đúng.
D. (I) và (II) sai.
Chọn C.
Lời giải
Véc tơ – không là véc tơ có điểm đầu, điểm cuối trùng nhau nên có độ dài bằng 0 .
Véc tơ – không cùng phương với mọi véc tơ.
Câu 789. [0H1-1] Cho hình vuông ABCD có cạnh bằng a. Độ dài \(|\overrightarrow {AD} + \overrightarrow {AB} |\) bằng
A. 2a
B. \(\frac{{a\sqrt 2 }}{2}\).
C. \(\frac{{a\sqrt 3 }}{2}\).
D. \(a\sqrt 2 \).
Lời giải
Chọn D.
Theo quy tắc đường chéo hình bình hành, ta có \(|\overrightarrow {AD} + \overrightarrow {AB} | = |\overrightarrow {AC} | = AC = AB\sqrt 2 = a\sqrt 2 \).
Câu 790. [0H1-1] Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm \(A(2; – 5)\) và \(B(4;1)\). Tọa độ trung điểm I của đoạn thẳng AB là
A. \(I(1;3)\).
B. \(I( – 1; – 3)\).
C. \(I(3;2)\).
D. \(I(3; – 2)\).
Lời giải
Chọn D.
Tọa độ trung điểm I của đoạn thẳng \(AB:\left\{ {\begin{array}{*{20}{l}}{{x_I} = \frac{{{x_A} + {x_B}}}{2}}\\{{y_I} = \frac{{{y_A} + {y_B}}}{2}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_I} = 3}\\{{y_I} = – 2}\end{array} \Rightarrow I(3; – 2)} \right.} \right.\).
Câu 791. [0H1-1] Cho tam giác ABC với \(A( – 2;3),B(4; – 1)\), trọng tâm của tam giác là \(G(2; – 1)\). Tọa độ đỉnh C là
A. \((6; – 4)\).
B. \((6; – 3)\).
C. \((4; – 5)\).
D. \((2;1)\).
Lời giải
Chọn C.
Do G là trọng tâm tam giácABC nên \(\left\{ {\begin{array}{*{20}{l}}{{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}}\\{{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_C} = 3{x_G} – {x_A} – {x_B}}\\{{y_C} = 3{y_G} – {y_A} – {y_B}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_C} = 4}\\{{y_C} = – 5}\end{array}.} \right.} \right.\)
Vậy \(C(4; – 5)\).
Câu 792. [0H1-1] Cho các điểm A,B,C,D và số thực k. Mệnh đề nào sau đây đúng?
A. \(AB = |k|CD \Rightarrow \overrightarrow {AB} = k\overrightarrow {CD} \).
B. \(AB = kCD \Rightarrow \overrightarrow {AB} = k\overrightarrow {CD} \).
C. \(\overrightarrow {AB} = k\overrightarrow {CD} \Rightarrow AB = |k|CD\).
D. \(\overrightarrow {AB} = k\overrightarrow {CD} \Rightarrow AB = kCD\).
Lời giải
Chọn C.
Theo định nghĩa phép nhân véc tơ với một số.
Câu 793. [0H1-1] Trong mặt phẳng với hệ tọa độ Oxy cho các điểm \(A(1;2),B(3; – 1),C(0;1)\). Tọa độ của véctơ \(\vec u = 2\overrightarrow {AB} + \overrightarrow {BC} \) là
A. \(\vec u = (2;2)\).
B. \(\vec u = ( – 4;1)\).
C. \(\vec u = (1; – 4)\).
D. \(\vec u = ( – 1;4)\).
Lời giải
Chọn C.
Ta có \(\overrightarrow {AB} = (2; – 3) \Rightarrow 2\overrightarrow {AB} = (4; – 6),\overrightarrow {BC} = ( – 3;2)\).
Nên \(\vec u = 2\overrightarrow {AB} + \overrightarrow {BC} = (1; – 4)\).
Câu 794. [0H1-1] Mệnh đề nào sau đây sai?
A. G là trọng tâm thì \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0\).
B. Ba điểm A,B,C bất kì thì \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} \).
C. I là trung điểm AB thì \(\overrightarrow {MI} = \overrightarrow {MA} + \overrightarrow {MB} \) với mọi điểm M.
D. ABCD là hình bình hành thì \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \).
Lời giải
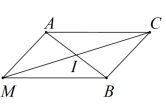
Chọn C.
Với mọi điểm M, ta dựng hình bình hành AMBC.
Khi đó, theo quy tắc hình bình hành: \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MC} = 2\overrightarrow {MI} \).
Câu 795. [0H1-1] Cho có trọng tâm G. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {AC} \).
B. \(\overrightarrow {AG} = 2(\overrightarrow {AB} + \overrightarrow {AC} )\).
C. \(\overrightarrow {AG} = \frac{1}{3}(\overrightarrow {AB} + \overrightarrow {AC} )\).
D. \(\overrightarrow {AG} = \frac{2}{3}(\overrightarrow {AB} + \overrightarrow {AC} )\).
Lời giải
Chọn C.
Gọi M là trung điểm BC, ta có: \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} = \frac{2}{3} \cdot \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} ) = \frac{1}{3}(\overrightarrow {AB} + \overrightarrow {AC} )\).
Câu 796. [0H1-1] Cho hai điểm \(A( – 3;1)\) và \(B(1; – 3)\). Tọa độ của vectơ \(\overrightarrow {AB} \) là
A. \(( – 2; – 2)\).
B. \(( – 1; – 1)\).
C. \((4; – 4)\).
D. \(( – 4;4)\).
Lời giải
Chọn C.
\(\overrightarrow {AB} = (1 – ( – 3); – 3 – 1) = (4; – 4){\rm{. }}\)
Câu 797. [0H1-1] Trong hệ tọa độ Oxy, cho \(\vec a = (3; – 4),\vec b = ( – 1;2)\). Tìm tọa độ của \(\vec a + \vec b\).
A. \(\vec a + \vec b = (4; – 6)\).
B. \(\vec a + \vec b = (2; – 2)\).
C. \(\vec a + \vec b = ( – 4;6)\).
D. \(\vec a + \vec b = ( – 3; – 8)\).
Lời giải
Chọn B.
\(\vec a + \vec b = (3 + ( – 1); – 4 + 2) = (2; – 2).\)
Câu 798. [0H1-1] Cho 5 điểm phân biệt M, N, P, Q, R. Mệnh đề nào sau đây đúng?
A. \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} = \overrightarrow {MP} \).
B. \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} = \overrightarrow {PR} \).
C. \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} = \overrightarrow {MR} \).
D. \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} = \overrightarrow {MN} \).
Lời giải
Chọn D.
Ta có \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} = \overrightarrow {MN} + \overrightarrow {NP} + \overrightarrow {PQ} + \overrightarrow {QR} + \overrightarrow {RN} = \overrightarrow {MN} \).
Câu 799. [0H1-1] Cho hình bình hành ABCD, đẳng thức véctơ nào sau đây đúng?
A. \(\overrightarrow {CD} + \overrightarrow {CB} = \overrightarrow {CA} \).
B. \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \).
C. \(\overrightarrow {BA} + \overrightarrow {BD} = \overrightarrow {BC} \).
D. \(\overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {AC} \).
Chọn A.
Lời giải
Đẳng thức véctơ \(\overrightarrow {CD} + \overrightarrow {CB} = \overrightarrow {CA} \) đúng theo quy tắc cộng hình bình hành.
Câu 800. [0H1-1] Cho tam giác đều ABC cạnh a, mệnh đề nào sau đây đúng?
A. \(|\overrightarrow {AC} | = \overrightarrow {BC} \).
B. \(\overrightarrow {AC} = a\).
C. \(\overrightarrow {AB} = \overrightarrow {AC} \).
D. \(|\overrightarrow {AB} | = a\).
Lời giải
Chọn D.
\(|\overrightarrow {AB} | = AB = a.\)
Câu 801. [0H1-1] Cho hình bình hành ABCD với I là giao điểm của hai đường chéo. Khẳng định nào sau đây là khẳng định sai?
A. \(\overrightarrow {IA} + \overrightarrow {IC} = \vec 0\).
B. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).
C. \(\overrightarrow {AB} = \overrightarrow {DC} \).
D. \(\overrightarrow {AC} = \overrightarrow {BD} \).
Chọn D.
Lời giải
ABCD là hình bình hành với I là giao điểm của hai đường chéo nên I là trung điểm của AC và BD nên ta có: \(\overrightarrow {IA} + \overrightarrow {IC} = \vec 0;\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} ;\overrightarrow {AB} = \overrightarrow {DC} \).
Câu 802. [0H1-1] Cho lục giác đều ABCDEF tâm O. Ba vectơ bằng vectơ \(\overrightarrow {BA} \) là
A. \(\overrightarrow {OF} ,\overrightarrow {DE} ,\overrightarrow {OC} \).
B. \(\overrightarrow {CA} ,\overrightarrow {OF} ,\overrightarrow {DE} \).
C. \(\overrightarrow {OF} ,\overrightarrow {DE} ,\overrightarrow {CO} \).
D. \(\overrightarrow {OF} ,\overrightarrow {ED} ,\overrightarrow {OC} \).
Lời giải
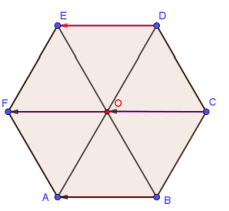
Chọn C.
Lời giải
Dựa vào hình vẽ ta có: \(\overrightarrow {BA} = \overrightarrow {CO} = \overrightarrow {OF} = \overrightarrow {DE} \).
Câu 803. [0H1-1] Cho hình bình hành ABCD có tâm O. Khẳng định nào sau đây là đúng:
A. \(\overrightarrow {AB} – \overrightarrow {AC} = \overrightarrow {DA} \).
B. \(\overrightarrow {AO} + \overrightarrow {AC} = \overrightarrow {BO} \).
C. \(\overrightarrow {AO} – \overrightarrow {BO} = \overrightarrow {CD} \).
D. \(\overrightarrow {AO} + \overrightarrow {BO} = \overrightarrow {BD} \).
Lời giải
Chọn A.
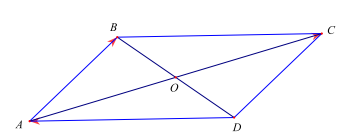
Ta có \(\overrightarrow {AB} – \overrightarrow {AC} = \overrightarrow {CB} \). Do ABCD là hình bình hành nên \(\overrightarrow {CB} = \overrightarrow {DA} \) nên \(\overrightarrow {AB} – \overrightarrow {AC} = \overrightarrow {DA} \).
Câu 804. [0H1-1] Cho \(\vec a = (1;2)\) và \(\vec b = (3;4)\). Vectơ \(\vec m = 2\vec a + 3\vec b\) có toạ độ là
A. \(\vec m = (10;12)\).
B. \(\vec m = (11;16)\).
C. \(\vec m = (12;15)\).
D. \(\vec m = (13;14)\).
Lời giải
Chọn B.
Ta có \(\vec m = 2\vec a + 3\vec b = (11;16)\).
Câu 805. [0H1-1] Cho ba điểm A,B,C phân biệt. Có tất cá bao nhiêu véctơ khác véctơ – không có điểm đầu, điểm cuối là hai điểm trong ba điểm A, B, C ?
A. 3 .
B. 4 .
C. 5 .
D. 6 .
Lời giải
Chọn D.
+ Có các véctơ: \(\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {AC} ,\overrightarrow {CA} ,\overrightarrow {BC} ,\overrightarrow {CB} \).
+ Vậy có 6 véctơ.
Câu 806. [0H1-1] Trong mặt phẳng tọa độ với hệ tọa độ Oxy, cho hai điểm \(A( – 2;3),B(1; – 6)\). Tọa độ của véctơ \(\overrightarrow {AB} \) bẳng
A. \(\overrightarrow {AB} = ( – 3;9)\).
B. \(\overrightarrow {AB} = ( – 1; – 3)\).
C. \(\overrightarrow {AB} = (3; – 9)\).
D. \(\overrightarrow {AB} = ( – 1; – 9)\).
Lời giải
Chọn C.
Ta có: \(\overrightarrow {AB} = (3; – 9)\).
Câu 807. [0H1-1] Trên mặt phẳng tọa độ Oxy cho hai vectơ \(\vec a = 2\vec i – 3\vec j,\vec b = \vec i + 2\vec j\). Khi đó tọa độ vectơ \(\vec a – \vec b\) là
A. \((2; – 1)\).
B. \((1;2)\).
C. \((1; – 5)\).
D. \((2; – 3)\).
Lời giải
Chọn C.
Ta có \(\vec a = 2\vec i – 3\vec j \Rightarrow \vec a = (2; – 3);\vec b = \vec i + 2\vec j \Rightarrow \vec b = (1;2)\) suy ra \(\vec a – \vec b = (1; – 5)\).
Câu 808. [0H1-1] Trên mặt phẳng tọa độ Oxy cho tam giác ABC có \(A(1;3),B( – 2;1)\) và \(C(0; – 3)\). Vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) có tọa độ là
A. (4;8)
B. (1;1)
C. (-1;-1)
D. (-4;-8)
Chọn D.
Lời giải
Ta có \(\overrightarrow {AB} = ( – 3; – 2);\overrightarrow {AC} = ( – 1; – 6)\).
Vậy \(\overrightarrow {AB} + \overrightarrow {AC} = ( – 4; – 8)\).
Câu 809. [0H1-1] Trên mặt phẳng toạ độ Oxy, cho \(A( – 2;5),B(1; – 1)\). Tìm toạ độ M sao cho \(\overrightarrow {MA} = – 2\overrightarrow {MB} \).
A. M(1;0)
B. M(0;-1)
C. M(-1;0).
D. M(0;1)
Lời giải:
Chọn D.
\(M(x;y)\).
\(\overrightarrow {MA} = – 2\overrightarrow {MB} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ – 2 – x = – 2(1 – x)}\\{5 – y = – 2( – 1 – y)}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}\\{y = 1}\end{array} \Rightarrow M(0;1).} \right.} \right.\)
Xem thêm