Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Chuyên đề công thức lượng giác và phương trình lượng giác
Chương 1: Công thúc lượng giác
I. Định nghĩa
Trên mặt phẳng Oxy cho đường tròn lượng giác tâm O bán kính R=1 và điểm M trên đường tròn lượng giác mà sđ với \(0 \le \beta \le 2\pi \)
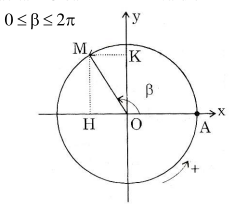
Đặt \(\alpha = \beta + {\rm{k}}2\pi ,{\rm{k}} \in {\rm{Z}}\)
Ta định nghĩa:
\(\sin \alpha = \overline {{\rm{OK}}} \) \(\cos \alpha = \overline {{\rm{OH}}} \)
\({\mathop{\rm tg}\nolimits} \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\) với \(\cos \alpha \ne 0\)
\({\mathop{\rm cotg}\nolimits} \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\) với \(\sin \alpha \ne 0\)
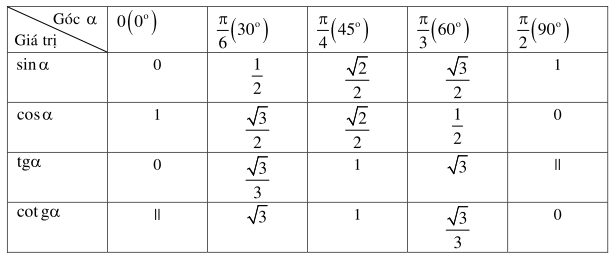
II. Bảng giá trị lượng giác của một số cung (hay góc) đặc biệt
III. Hệ thức cơ bản
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
\(\begin{array}{l}1 + {{\mathop{\rm tg}\nolimits} ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}{\rm{ voi }}\alpha \ne \frac{\pi }{2} + {\rm{k}}\pi ({\rm{k}} \in {\rm{Z}})\\{\rm{t}} + \cot {{\rm{g}}^2} = \frac{1}{{{{\sin }^2}\alpha }}{\rm{ voi }}\alpha \ne {\rm{k}}\pi ({\rm{k}} \in {\rm{Z}})\end{array}\)
IV. Cung liên kết ( Cách nhớ: cos đối, sin bù, tang sai \(\pi \), phụ chéo)
a. Đối nhau: \(\alpha \) và \[ – \alpha \]
\[\begin{array}{l}\sin ( – \alpha ) = – \sin \alpha \\\cos ( – \alpha ) = \cos \alpha \\{\mathop{\rm tg}\nolimits} ( – \alpha ) = – {\mathop{\rm tg}\nolimits} (\alpha )\\{\mathop{\rm cotg}\nolimits} ( – \alpha ) = – \cot g(\alpha )\end{array}\]
b. Bù nhau: \(\alpha \) và \(\pi – \alpha \)
\(\begin{array}{l}\sin (\pi – \alpha ) = \sin \alpha \\\cos (\pi – \alpha ) = – \cos \alpha \\{\mathop{\rm tg}\nolimits} (\pi – \alpha ) = – {\mathop{\rm tg}\nolimits} \alpha \\{\mathop{\rm cotg}\nolimits} (\pi – \alpha ) = – \cot g\alpha \end{array}\)
c. Sai nhau \(\pi \) : \(\alpha \) và \(\pi + \alpha \)
\[\begin{array}{l}\sin (\pi + \alpha ) = – \sin \alpha \\\cos (\pi + \alpha ) = – \cos \alpha \\{\mathop{\rm tg}\nolimits} (\pi + \alpha ) = {\mathop{\rm tg}\nolimits} \alpha \\{\mathop{\rm cotg}\nolimits} (\pi + \alpha ) = {\mathop{\rm cotg}\nolimits} \alpha \end{array}\]
d. Phụ nhau: \(\alpha \) và \(\frac{\pi }{2} – \alpha \)
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} – \alpha } \right) = \cos \alpha \\\cos \left( {\frac{\pi }{2} – \alpha } \right) = \sin \alpha \\{\mathop{\rm tg}\nolimits} \left( {\frac{\pi }{2} – \alpha } \right) = {\mathop{\rm cotg}\nolimits} \alpha \\{\mathop{\rm cotg}\nolimits} \left( {\frac{\pi }{2} – \alpha } \right) = {\mathop{\rm tg}\nolimits} \alpha \end{array}\)
e.Sai nhau \(\frac{\pi }{2}:\alpha \) và \(\frac{\pi }{2} + \alpha \)
\(\sin \left( {\frac{\pi }{2} + \alpha } \right) = \cos \alpha \)
\(\cos \left( {\frac{\pi }{2} + \alpha } \right) = – \sin \alpha \)
\({\mathop{\rm tg}\nolimits} \left( {\frac{\pi }{2} + \alpha } \right) = – {\mathop{\rm cotg}\nolimits} \alpha \)
\(\cot g\left( {\frac{\pi }{2} + \alpha } \right) = – {\mathop{\rm tg}\nolimits} \alpha \)
f.
\(\sin (x + k\pi ) = {( – 1)^k}\sin x,k \in Z\)
\(\cos (x + k\pi ) = {( – 1)^k}\cos x,k \in Z\)
\({\mathop{\rm tg}\nolimits} (x + k\pi ) = {\mathop{\rm tg}\nolimits} x,k \in Z\)
\(\cot g(x + k\pi ) = \cot gx\)
V. Công thức cộng
\(\begin{array}{l}\sin (a \pm b) = \sin a\cos b \pm \sin b\cos a\\\cos (a \pm b) = \cos a\cos b \mp \sin a\sin b\\{\mathop{\rm tg}\nolimits} (a \pm b) = \frac{{{\mathop{\rm tg}\nolimits} a \pm {\mathop{\rm tg}\nolimits} b}}{{1 \mp {\mathop{\rm tg}\nolimits} a{\mathop{\rm tg}\nolimits} b}}\end{array}\)$
VI. Công thức nhân đôi
\[\begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a – {\sin ^2}a = 1 – 2{\sin ^2}a = 2{\cos ^2}a – 1\\{\mathop{\rm tg}\nolimits} 2a = \frac{{2{\mathop{\rm tg}\nolimits} a}}{{1 – {{{\mathop{\rm tg}\nolimits} }^2}a}}\\{\mathop{\rm cotg}\nolimits} 2a = \frac{{\cot {g^2}a – 1}}{{2\cot ga}}\end{array}\]
VII. Công thức nhân ba:
\(\begin{array}{l}\sin 3a = 3\sin a – 4{\sin ^3}a\\\cos 3a = 4{\cos ^3}a – 3\cos a\end{array}\)
VIII. Công thức hạ bậc:
\(\begin{array}{l}{\sin ^2}a = \frac{1}{2}(1 – \cos 2a)\\{\cos ^2}a = \frac{1}{2}(1 + \cos 2a)\\{{\mathop{\rm tg}\nolimits} ^2}a = \frac{{1 – \cos 2a}}{{1 + \cos 2a}}\end{array}\)$
IX. Công thức chia đôi
Đặt\({\rm{ t}} = {\mathop{\rm tg}\nolimits} \frac{{\rm{a}}}{2}{\rm{ }}\)(với \({\rm{ a}} \ne \pi + {\rm{k}}2\pi {\rm{ ) }}\)
\(\begin{array}{l}\sin a = \frac{{2t}}{{1 + {t^2}}}\\\cos a = \frac{{1 – {t^2}}}{{1 + {t^2}}}\\{\mathop{\rm tg}\nolimits} a = \frac{{2t}}{{1 – {t^2}}}\end{array}\)
X. Công thức biến đổi tổng thành tích
\(\begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a – b}}{2}\\\cos a – \cos b = – 2\sin \frac{{a + b}}{2}\sin \frac{{a – b}}{2}\\\sin a + \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a – b}}{2}\\\sin a – \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a – b}}{2}\\{\mathop{\rm tg}\nolimits} a \pm {\mathop{\rm tg}\nolimits} b = \frac{{\sin (a \pm b)}}{{\cos a\cos b}}\\\cot ga \pm \cot gb = \frac{{\sin (b \pm a)}}{{\sin a \cdot \sin b}}\end{array}\)
XI. Công thức biển đổi tích thành tổng
\(\begin{array}{l}\cos a \cdot \cos b = \frac{1}{2}[\cos (a + b) + \cos (a – b)]\\\sin a \cdot \sin b = \frac{{ – 1}}{2}[\cos (a + b) – \cos (a – b)]\\\sin a \cdot \cos b = \frac{1}{2}[\sin (a + b) + \sin (a – b)]\end{array}\)
Bài 1. Chứng minh \(\frac{{{{\sin }^4}a + {{\cos }^4}a – 1}}{{{{\sin }^6}a + {{\cos }^6}a – 1}} = \frac{2}{3}\)
Ta có:
\({\sin ^4}a + {\cos ^4}a – 1 = {\left( {{{\sin }^2}a + {{\cos }^2}a} \right)^2} – 2{\sin ^2}a{\cos ^2}a – 1 = – 2{\sin ^2}a{\cos ^2}a\)
Và:
\({\sin ^6}a + {\cos ^6}a – 1 = \left( {{{\sin }^2}a + {{\cos }^2}a} \right)\left( {{{\sin }^4}a – {{\sin }^2}a{{\cos }^2}a + {{\cos }^4}a} \right) – 1\)
\( = {\sin ^4}a + {\cos ^4}a – {\sin ^2}a{\cos ^2}a – 1\)
\( = \left( {1 – 2{{\sin }^2}a{{\cos }^2}a} \right) – {\sin ^2}a{\cos ^2}a – 1\)
\( = – 3{\sin ^2}a{\cos ^2}a\)
Do đó: \(\frac{{{{\sin }^4}a + {{\cos }^4}a – 1}}{{{{\sin }^6}a + {{\cos }^6}a – 1}} = \frac{{ – 2{{\sin }^2}a{{\cos }^2}a}}{{ – 3{{\sin }^2}a{{\cos }^2}a}} = \frac{2}{3}\)
Bài 2: Rút gọn biểu thức \(A = \frac{{1 + \cos x}}{{\sin x}} = \left[ {1 + \frac{{{{(1 – \cos x)}^2}}}{{{{\sin }^2}x}}} \right]\)
Tính giá trị A nếu \(\cos x = – \frac{1}{2}\) và \(\frac{\pi }{2} < x < \pi \)
Ta có: \(A = \frac{{1 + \cos x}}{{\sin x}}\left( {\frac{{{{\sin }^2}x + 1 – 2\cos x + {{\cos }^2}x}}{{{{\sin }^2}x}}} \right)\)
\( \Leftrightarrow A = \frac{{1 + \cos x}}{{\sin x}} \cdot \frac{{2(1 – \cos x)}}{{{{\sin }^2}x}}\)
\( \Leftrightarrow A = \frac{{2\left( {1 – {{\cos }^2}x} \right)}}{{{{\sin }^3}x}} = \frac{{2{{\sin }^2}x}}{{{{\sin }^3}x}} = \frac{2}{{\sin x}}(\) với \(\sin x \ne 0)\)
Ta có: \({\sin ^2}x = 1 – {\cos ^2}x = 1 – \frac{1}{4} = \frac{3}{4}\)
Do: \(\frac{\pi }{2} < x < \pi \) nên \(\sin x > 0\)
Vậy \(\sin x = \frac{{\sqrt 3 }}{2}\)
Do đó \(A = \frac{2}{{\sin x}} = \frac{4}{{\sqrt 3 }} = \frac{{4\sqrt 3 }}{3}\)
Bài 3. Chứng minh các biểu thức sau đây không phụ thuộc x :
a. \(A = 2{\cos ^4}x – {\sin ^4}x + {\sin ^2}x{\cos ^2}x + 3{\sin ^2}x\)
b. \(B = \frac{2}{{{\mathop{\rm tg}\nolimits} x – 1}} + \frac{{{\mathop{\rm cotg}\nolimits} x + 1}}{{{\mathop{\rm cotg}\nolimits} x – 1}}\)
a. Ta có:
\(A = 2{\cos ^4}x – {\sin ^4}x + {\sin ^2}x{\cos ^2}x + 3{\sin ^2}x\)
\( \Leftrightarrow {\rm{A}} = 2{\cos ^4}{\rm{x}} – {\left( {1 – {{\cos }^2}{\rm{x}}} \right)^2} + \left( {1 – {{\cos }^2}{\rm{x}}} \right){\cos ^2}{\rm{x}} + 3\left( {1 – {{\cos }^2}{\rm{x}}} \right)\)
\( \Leftrightarrow A = 2{\cos ^4}x – \left( {1 – 2{{\cos }^2}x + {{\cos }^4}x} \right) + {\cos ^2}x – {\cos ^4}x + 3 – 3{\cos ^2}x\)
\( \Leftrightarrow A = 2\) (không phụ thuộc x )
b. Với điều kiện \(\sin x \cdot \cos x \ne 0,{\mathop{\rm tg}\nolimits} x \ne 1\)
Ta có: \(B = \frac{2}{{{\mathop{\rm tg}\nolimits} x – 1}} + \frac{{\cot gx + 1}}{{\cot gx – 1}}\)
\( \Leftrightarrow B = \frac{2}{{{\mathop{\rm tg}\nolimits} x – 1}} + \frac{{\frac{1}{{{\mathop{\rm tg}\nolimits} x}} + 1}}{{\frac{1}{{{\mathop{\rm tg}\nolimits} x}} – 1}} = \frac{2}{{{\mathop{\rm tg}\nolimits} x – 1}} + \frac{{1 + {\mathop{\rm tg}\nolimits} x}}{{1 – {\mathop{\rm tg}\nolimits} x}}\)
\( \Leftrightarrow B = \frac{{2 – (1 – {\mathop{\rm tg}\nolimits} x)}}{{{\mathop{\rm tg}\nolimits} x – 1}} = \frac{{1 – {\mathop{\rm tg}\nolimits} x}}{{{\mathop{\rm tg}\nolimits} x – 1}} = – 1\) (không phụ thuộc vào x )
Xem thêm