Lý thuyết Toán lớp 10 Bài 3: Dấu của tam thức bậc hai
Video giải Toán 10 Bài 3: Dấu của tam thức bậc hai – Cánh diều
A. Lý thuyết Dấu của tam thức bậc hai
1. Dấu của tam thức bậc hai
Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0), ∆ = b2 – 4ac.
+ Nếu ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ ℝ
+ Nếu ∆ = 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ ℝ \
+ Nếu ∆ > 0 thì f(x) có hai nghiệm x1, x2 (x1 < x2). Khi đó:
– f(x) cùng dấu với hệ số a với mọi x thuộc các khoảng (–∞; x1); (x2; +∞)
– f(x) trái dấu với hệ số a với mọi x thuộc khoảng (x1; x2).
2. Ví dụ
2.1. Ví dụ 1
Xét dấu của tam thức bậc hai
a) f(x) = 4x2 – x + 1;
b) f(x) = x2 + 2x + 1.
Hướng dẫn giải
a) Tam thức bậc hai f(x) = 4x2 – x + 1 có ∆ = b2 – 4ac = (– 1)2 – 4.4.1 = –15 < 0, hệ số
a = 4 > 0 nên f(x) > 0 với mọi x ∈ ℝ.
b) Tam thức bậc hai f(x) = x2 + 2x + 1 có ∆ = b2 – 4ac = 22 – 4.1.1 = 0, hệ số a = 1 > 0, nghiệm kép x0 = – 1 nên f(x) > 0 với mọi x ∈ ℝ \ {– 1}.
2.2. Ví dụ 2
Lập bảng xét dấu của tam thức bậc hai f(x) = x2 – 4x + 3.
Hướng dẫn giải
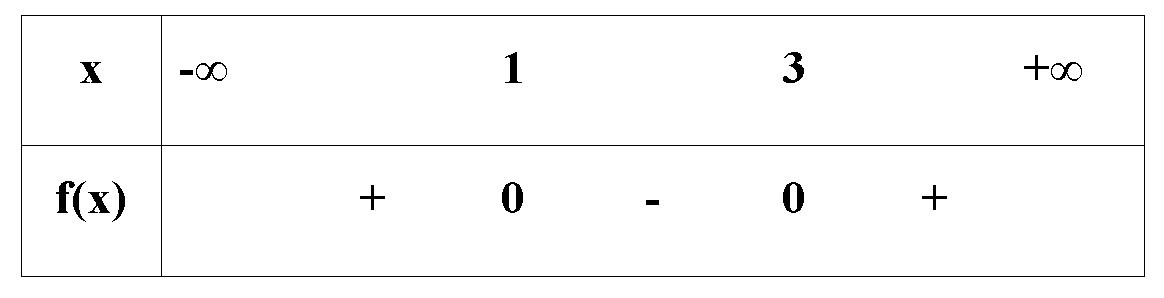
Tam thức bậc hai f(x) = x2 – 4x + 3 có ∆ = b2 – 4ac = (– 4)2 – 4.1.3 = 4 > 0 có hai nghiệm phân biệt x1 = 1; x2 = 3; hệ số a = 1 > 0.
Ta có bảng xét dấu như sau:
B. Bài tập tự luyện
B.1 Bài tập tự luận
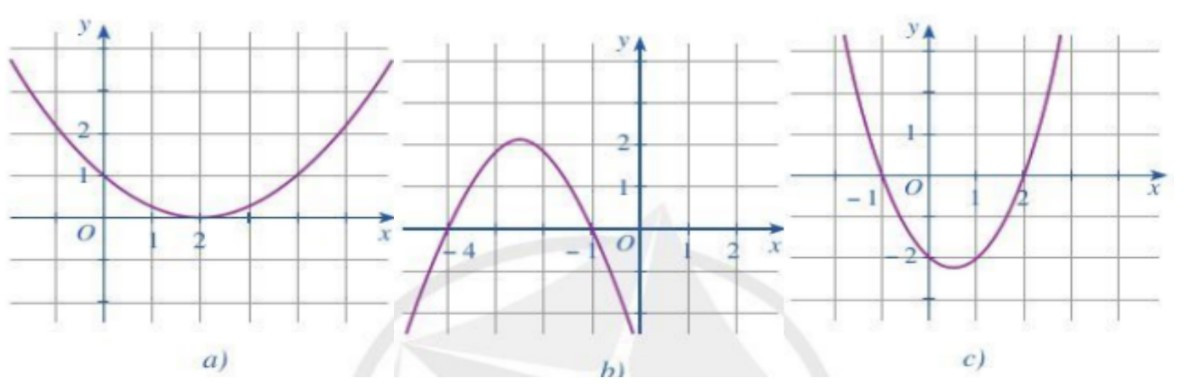
Bài 1. Tìm nghiệm và lập bảng xét dấu của tam thức bậc hai với đồ thị được cho ở mỗi hình.
Hướng dẫn giải
a)
Ta thấy đồ thị cắt trục Ox tại điểm (2; 0) nên phương trình f(x) = 0 có duy nhất nghiệm x = 2.
Ta thấy đồ thị nằm trên trục hoành nên ta có bảng xét dấu:

b)
Ta thấy đồ thị cắt trục Ox tại hai điểm phân biệt (–4; 0) và (–1; 0) nên phương trình
f(x) = 0 có hai nghiệm phân biệt x1 = –4; x2 = –1.
Trong các khoảng (–∞; –4) và (–1; +∞) thì đồ thị nằm dưới trục hoành nên f(x) < 0, trong khoảng (–4; –1) thì đồ thị nằm trên trục hoành nên f(x) > 0.
Bảng xét dấu:

c)
Ta thấy đồ thị cắt trục Ox tại hai điểm phân biệt (–1; 0) và (2; 0) nên phương trình
f(x) = 0 có hai nghiệm phân biệt x1 = –1; x2 = 2
Trong các khoảng (–∞; –1) và (2; +∞) thì đồ thị nằm trên trục hoành nên f(x) > 0
Trong khoảng (–1; 2) thì đồ thị nằm dưới trục hoành nên f(x) < 0.
Bảng xét dấu:

Bài 2. Khi nào thì tam thức bậc hai nhận giá trị dương.
Hướng dẫn giải
Ta có: .
Bảng xét dấu:
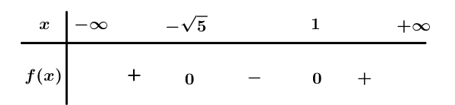
Dựa vào bảng xét dấu
Bài 3. Tìm giá trị nguyên của x để tam thức f(x) = 2x2 – 7x – 9 nhận giá trị âm.
Hướng dẫn giải
Ta có: .
Bảng xét dấu
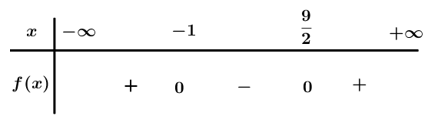
Dựa vào bảng xét dấu . Mà x nguyên nên x ∈ {0 ; 1 ; 2 ; 3 ; 4}.
Như vậy, với x nguyên x ∈ {0 ; 1 ; 2 ; 3 ; 4} thì f(x) = 2x2 – 7x – 9 < 0.
B.2 Bài tập trắc nghiệm
Câu 1.Tam thức bậc hai nhận giá trị không âm khi và chỉ khi
A.;
B. ;
C. .
D. .
Hướng dẫn giải
Đáp án đúng là: B
Ta có: .
Bảng xét dấu
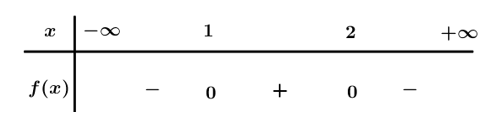
Dựa vào bảng xét dấu .
Do đó, .
Câu 2. Tam thức bậc hai nhận giá trị dương khi và chỉ khi
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án đúng là: D
Ta có: .
Bảng xét dấu
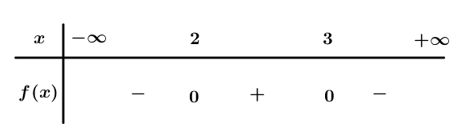
Dựa vào bảng xét dấu
Câu 3. Cho các tam thức . Số tam thức đổi dấu trên ℝ là:
A. 0;
B. 1;
C. 2;
D. 3.
Hướng dẫn giải
Đáp án đúng là: B
Vì f(x) = 0 vô nghiệm, g(x) = 0 vô nghiệm, h(x) = 0 có hai nghiệm phân biệt nên chỉ có h(x) đổi dấu trên ℝ.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
Lý thuyết Bài 3: Dấu của tam thức bậc hai
Lý thuyết Bài 4: Bất phương trình bậc hai một ẩn
Lý thuyết Bài 5: Hai dạng phương trình quy về phương trình bậc hai
Lý thuyết Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác
Bài giảng Toán 10 Bài 3: Dấu của tam thức bậc hai – Cánh diều