30 câu Trắc nghiệm Toán 10 Chương 10: Xác suất (Chân trời sáng tạo 2023) có đáp án

Trắc nghiệm Toán 10 Chương 10: Xác suất

I. Nhận biết

Câu 1. Biến cố không bao giờ xảy ra là:

A. Biến cố không thể;             

B. Biến cố chắc chắn;             

C. Phép thử;                  

D. Không gian mẫu.

Hướng dẫn giải

Đáp án: A

Giải thích:

⦁ Biến cố chắc chắn là biến cố luôn xảy ra, kí hiệu là Ω. Do đó phương án B sai.

⦁ Biến cố không thể là biến cố không bao giờ xảy ra, kí hiệu là ∅. Do đó phương án A đúng.

⦁ Phép thử ngẫu nhiên (gọi tắt là phép thử) là một hoạt động mà ta không thể biết trước được kết quả của nó. Do đó phương án C sai.

⦁ Tập hợp tất cả các kết quả có thể có của phép thử ngẫu nhiên được gọi là không gian mẫu. Do đó phương án D sai.

Vậy ta chọn phương án A.

Câu 2. Cho biến cố A có không gian mẫu Ω và $\bar{A}$ là biến cố đối của biến cố A. Khẳng định nào sau đây sai?

A. n(Ω) = P(A).n(A);              

B. $A=\Omega \backslash \overline{A}$;                

C. $P\left(\overline{A}\right)+P\left(A\right)=P\left(\Omega \right)$;                  

D. n(A) = P(A).n(Ω).

Hướng dẫn giải

Đáp án: A

Giải thích:

⦁ Xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}$.

Suy ra $n\left(\Omega \right)=\frac{n\left(A\right)}{P\left(A\right)}$ và n(A) = P(A).n(Ω).

Vì vậy phương án A sai, phương án D đúng.

⦁ Ta có $P\left(\overline{A}\right)+P\left(A\right)=1$ nên  $A=\Omega \backslash \overline{A}$. Do đó phương án B đúng.

⦁ Ta có $P\left(\overline{A}\right)+P\left(A\right)=1$ và P(Ω) = 1.

Suy ra $P\left(\overline{A}\right)+P\left(A\right)=P\left(\Omega \right)$. Do đó phương án C đúng.

Vậy ta chọn phương án A.

Câu 3. Nguyên lí xác suất bé được phát biểu như thế nào?

A. Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó có xác suất bằng 0;                  

B. Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó không chắc sẽ xảy ra;                  

C. Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó chắc chắn sẽ xảy ra;                  

D. Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó sẽ không xảy ra.

Hướng dẫn giải

Đáp án: D

Giải thích:

Theo Lí thuyết Xác suất, Nguyên lí xác suất bé được phát biểu như sau:

Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó sẽ không xảy ra.

Vậy ta chọn phương án D.

Câu 4. Mệnh đề nào sau đây đúng?

A. Biến cố chắc chắn là biến cố không bao giờ xảy ra;           

B. Mỗi tập con của không gian mẫu được gọi là một biến cố;          

C. Một kết quả thuộc biến cố A được gọi là kết quả làm cho biến cố A không xảy ra;

D. Biến cố có khả năng xảy ra càng cao thì xác suất của nó càng gần 0.

Hướng dẫn giải

Đáp án: B

Giải thích:

Phương án A sai, vì biến cố chắc chắn là biến cố luôn xảy ra.

Phương án B đúng.

Phương án C sai, vì một kết quả thuộc biến cố A được gọi là kết quả làm cho biến cố A xảy ra, hoặc kết quả thuận lợi cho biến cố A.

Phương án D sai, vì biến cố có khả năng xảy ra càng cao thì xác suất của nó càng gần 1.

Vậy ta chọn phương án B.

Câu 5. Một hộp chứa 4 quả cầu trắng và 6 quả cầu xanh có kích thước và khối lượng như nhau. Lấy ngẫu nhiên 3 quả cầu từ trong hộp. Hoạt động nào sau đây không phải là biến cố của phép thử trên?

A. Ba quả cầu lấy ra cùng màu với nhau;           

B. Ba quả cầu lấy ra có ít nhất một quả màu trắng;               

C. Ba quả cầu lấy ra gồm có ba màu;                  

D. Ba quả cầu lấy ra có nhiều nhất hai quả cầu màu xanh.

Hướng dẫn giải

Đáp án: C

Giải thích:

Ta thấy các quả cầu trong hộp chỉ có hai màu là trắng và xanh nên phép thử trên không thể có biến cố: “Ba quả cầu lấy ra gồm có ba màu” được.

Do đó hoạt động của phương án C không phải là biến cố của phép thử đã cho.

Vậy ta chọn phương án C.

Câu 6. Cho biến cố A có không gian mẫu là Ω và $\overline{A}$ là biến cố đối của biến cố A. Khẳng định nào sau đây sai?

A. P(A) ≥ 0, với mọi biến cố A;                 

B. P(∅) = 0;         

C. P(Ω) > 1;                  

D. P(A) ≤ 1, với mọi biến cố A.

Hướng dẫn giải

Đáp án: C

Giải thích:

⦁ Với mọi biến cố A, ta có 0 ≤ P(A) ≤ 1.

Do đó phương án A, D đúng.

⦁ P(Ω) = 1 và P(∅) = 0.

Do đó phương án B đúng, phương án C sai.

Vậy ta chọn phương án C.

Câu 7. Lấy ngẫu nhiên hai viên bi từ một thùng có 4 bi xanh, 5 bi đỏ và 6 bi vàng. Số phần tử của không gian mẫu là:

A. 30;                  

B. 17;                  

C. 105;                

D. 210.

Hướng dẫn giải

Đáp án: C

Giải thích:

Trong thùng có tổng cộng 4 + 5 + 6 = 15 (viên bi).

Lấy ngẫu nhiên hai viên bi trong số 15 viên bi trong thùng mà không quan tâm đến thứ tự thì có $C_{15}^2=105$ (cách chọn).

Vậy số phần tử của không gian mẫu là: n(Ω) = 105.

Do đó ta chọn phương án C.

Câu 8. Một cầu thủ sút bóng vào cầu môn một lần. Biết rằng xác suất sút vào cầu môn là $\frac{3}{8}$. Xác suất không sút vào cầu môn của cầu thủ đó bằng:

A. $\frac{3}{8}$;         

B. $\frac{5}{8}$;         

C. $\frac{1}{2}$;         

D. 0.

Hướng dẫn giải

Đáp án: B

Giải thích:

Gọi A: “Cầu thủ sút vào cầu môn”.

Ta có biến cố không sút vào cầu môn của cầu thủ là biến cố đối của biến cố sút vào cầu môn.

Suy ra $\overline{A}$: “Cầu thủ không sút vào cầu môn”.

Khi đó $P\left(\overline{A}\right)=1-P\left(A\right)=1-\frac{3}{8}=\frac{5}{8}$.

Vậy ta chọn phương án B.

Câu 9. Hai xạ thủ bắn vào một tấm bia, xác suất bắn trúng bia của xạ thủ 1 và 2 lần lượt là 0,8 và 0,7. Xạ thủ nào có khả năng bắn trúng thấp hơn?

A. Xạ thủ 1;                  

B. Xạ thủ 2;                  

C. Cả hai xạ thủ đều có khả năng bắn trúng như nhau;          

D. Không thể xác định được.

Hướng dẫn giải

Đáp án: B

Giải thích:

Vì 0,8 > 0,7 nên xạ thủ 2 có khả năng bắn trúng bia thấp hơn xạ thủ 1.

Vậy ta chọn phương án B.

Câu 10. Cho phép thử có không gian mẫu là Ω = {1; 2; 3; 4; 5; 6}. Các cặp biến cố không đối nhau là:

A. A = {1} và B = {2; 3; 4; 5; 6};              

B. C = {1; 4; 5} và D = {2; 3; 6};              

C. E = {1; 4; 6} và F = {2; 3};         

D. Ω và ∅.

Hướng dẫn giải

Đáp án: C

Giải thích:

⦁ Xét phương án A: Ω = {1; 2; 3; 4; 5; 6}.

Ta có biến cố A = {1} có biến cố đối là: $\overline{A}$ = {2; 3; 4; 5; 6} = B.

Do đó biến cố A và biến cố B đối nhau.

⦁ Xét phương án B: Ω = {1; 2; 3; 4; 5; 6}.

Ta có biến cố C = {1; 4; 5} có biến cố đối là: $\overline{C}$ = {2; 3; 6} = D.

Do đó biến cố C và biến cố D đối nhau.

⦁ Xét phương án C: Ω = {1; 2; 3; 4; 5; 6}.

Ta có biến cố E = {1; 4; 6} có biến cố đối là: $\overline{E}$ = {2; 3; 5} ≠ F.

Do đó biến cố E và biến cố F không đối nhau.

⦁ Xét phương án D: Ω = {1; 2; 3; 4; 5; 6}.

Ta có biến cố đối của không gian mẫu Ω là ∅.

Do đó Ω và ∅ là hai biến cố đối nhau.

Vậy ta chọn phương án C.

II. Thông hiểu

Câu 1. Từ một hộp chứa 11 quả cầu đỏ và 4 quả cầu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được 3 quả cầu màu xanh là:

A. $\frac{4}{165}$;               

B. $\frac{4}{455}$;               

C. $\frac{33}{91}$;                 

D. $\frac{24}{455}$.

Hướng dẫn giải

Đáp án: B

Giải thích:

Có tất cả 11 + 4 = 15 quả cầu trong hộp.

Lấy ngẫu nhiên đồng thời 3 quả cầu (không tính đến thứ tự) thì có $C_{15}^3=455$ cách chọn.

Tức là n(Ω) = 455.

Gọi biến cố A: “Lấy được 3 quả cầu màu xanh”.

Lấy ngẫu nhiên 3 quả cầu xanh trong 4 quả cầu xanh (không tính đến thứ tự) thì có $C_4^3=4$ cách chọn.

Tức là n(A) = 4.

Vậy xác suất để lấy được 3 quả cầu màu xanh là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{4}{455}$.

Ta chọn phương án B.

Câu 2. Tung một đồng tiền và gieo một con xúc xắc một lần. Số phần tử của không gian mẫu là:

A. 24;                  

B. 12;                  

C. 6;           

D. 8.

Hướng dẫn giải

Đáp án: B

Giải thích:

Ta kí hiệu S nếu tung đồng tiền được mặt sấp và kí hiệu N nếu tung được mặt ngửa.

Mô tả không gian mẫu của phép thử trên, ta có:

Ω = {S1; S2; S3; S4; S5; S6; N1; N2; N3; N4; N5; N6}.

Khi đó số phần tử của không gian mẫu là: n(Ω) = 12.

Vậy ta chọn phương án B.

Câu 3. Gieo ngẫu nhiên một xúc xắc 6 mặt cân đối và đồng chất. Xác suất của biến cố A: “Mặt xuất hiện có số chấm chia hết cho 3” là:

A. 1;          

B. $\frac{1}{2}$;         

C. $\frac{1}{3}$;         

D. $\frac{2}{3}$.

Hướng dẫn giải

Đáp án: C

Giải thích:

Không gian mẫu của biến cố đã cho là Ω = {1; 2; 3; 4; 5; 6}.

Suy ra n(Ω) = 6.

Trong các số 1; 2; 3; 4; 5; 6, ta có các số chia hết cho 3 là: 3; 6.

Suy ra n(A) = 2.

Khi đó xác suất của biến cố A là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{2}{6}=\frac{1}{3}$.

Vậy ta chọn phương án C.

Câu 4. Một bể cá gồm 5 con cá Koi và 7 con cá vàng. Một người vớt ngẫu nhiên 4 con cá từ bể cá đó. Số kết quả thuận lợi của biến cố X: “Vớt được 2 con cá Koi và 2 con cá vàng” là:

A. 210;                

B. 201;                

C. 31;                  

D. 495.

Hướng dẫn giải

Đáp án: A

Giải thích:

Vớt ngẫu nhiên được 2 con cá Koi trong số 5 con cá Koi và không tính đến thứ tự thì có $C_5^2$ cách vớt.

Với ngẫu nhiên được 2 con cá vàng trong số 7 con cá vàng và không tính đến thứ tự thì có $C_7^2$ cách vớt.

Theo quy tắc nhân, ta có số kết quả thuận lợi của biến cố X là: $C_5^2.C_7^2$ = 210.

Vậy ta chọn phương án A.

Câu 5. Gieo một đồng xu cân đối và đồng chất ba lần. Xét biến cố A: “Mặt ngửa xuất hiện ít nhất 1 lần”. Tập hợp nào sau đây mô tả biến cố A?

A. A = {SSN, NSS, SNN, NNS, NNN};             

B. A = {SSN, SNS, NSS, NNN};              

C. A = {SSN, SNS, NSS, SNN, NSN, NNS, NNN};             

D. A = { SSN, SNS, NSS}.

Hướng dẫn giải

Đáp án: C

Giải thích:

Ta kí hiệu S nếu tung được mặt sấp, kí hiệu N nếu tung được mặt ngửa.

Trường hợp 1: Mặt ngửa xuất hiện đúng 1 lần.

Khi đó tập hợp A chứa các phần tử: SSN, SNS, NSS.

Trường hợp 2: Mặt ngửa xuất hiện đúng 2 lần.

Khi đó tập hợp A chứa phần tử: SNN, NSN, NNS.

Trường hợp 3: Mặt ngửa xuất hiện cả 3 lần.

Khi đó tập hợp A chứa phần tử: NNN.

Kết hợp cả 3 trường hợp trên, ta có tập hợp A là:

A = {SSN, SNS, NSS, SNN, NSN, NNS, NNN}.

Vậy ta chọn phương án C.

Câu 6. Trong hộp có 2 000 nắp khoen bia Tiger, trong đó có 2 nắp ghi “Chúc mừng bạn đã trúng thưởng xe Ford”. Bạn được chọn lên rút thăm lần lượt hai nắp khoen. Xác suất để cả hai nắp khoen đều trúng thưởng là:

A. $\frac{1}{1999000}$;                

B. $\frac{1}{2000}$;            

C. $\frac{1}{999500}$;                  

D. $\frac{1}{1000}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

Chọn 2 nắp khoen trong số 2 000 nắp khoen trong hộp và không tính đến thứ tự thì có $C_{2000}^2=1999000$ cách chọn.

Suy ra số phần tử của không gian mẫu là: n(Ω) = 1 999 000.

Chọn được cả 2 nắp khoen trúng thưởng trong số 2 nắp khoen trúng thưởng thì có 1 cách chọn.

Vậy xác suất của biến cố đã cho là: $\frac{1}{1999000}$.

Ta chọn phương án A.

Câu 7. Trong giỏ có 5 đôi tất khác màu, các chiếc tất cùng đôi thì cùng màu. Lấy ngẫu nhiên 2 chiếc tất. Xác suất để 2 chiếc đó cùng màu là:

A. $\frac{1}{24}$;                 

B. $\frac{1}{18}$;                 

C. $\frac{1}{9}$;         

D. $\frac{1}{5}$.

Hướng dẫn giải

Đáp án: C

Giải thích:

Gọi biến cố M: “Lấy ra 2 chiếc tất cùng màu”.

Trong giỏ có 5 đôi tất. Ta suy ra trong giỏ có tổng cộng 10 chiếc tất.

Lấy ngẫu nhiên hai chiếc tất trong số 10 chiếc tất trong giỏ (không tính đến thứ tự) thì có $C_{10}^2=45$.

Suy ra số phần tử của không gian mẫu là: n(Ω) = 45.

Lấy 2 chiếc tất cùng màu từ 10 chiếc tất trong giỏ tức là lấy ra 2 chiếc tất cùng đôi từ giỏ chứa 5 đôi tất.

Khi đó số cách lấy là: $C_5^1=5$.

Suy ra n(M) = 5.

Vậy xác suất của biến cố M là: $P\left(M\right)=\frac{n\left(M\right)}{n\left(\Omega \right)}=\frac{5}{45}=\frac{1}{9}$.

Ta chọn phương án C.

Câu 8. Trên giá sách có 4 quyển sách Toán, 3 quyển sách Vật lí và 2 quyển sách Hóa học. Lấy ngẫu nhiên 3 quyển sách. Xác suất để trong 3 quyển sách được lấy ra có ít nhất một quyển sách Toán là:

A. $\frac{3}{4}$;         

B. $\frac{2}{7}$;         

C. $\frac{10}{21}$;                 

D. $\frac{37}{42}$.

Hướng dẫn giải

Đáp án: D

Giải thích:

Trên giá sách có tất cả 4 + 3 + 2 = 9 quyển sách.

Lấy ngẫu nhiên 3 quyển sách trong số 9 quyển sách và không tính đến thứ tự thì có $C_9^3=84$ cách chọn.

Tức là n(Ω) = 84.

Gọi biến cố E: “Trong 3 quyển sách được lấy ra có ít nhất một quyển sách Toán”.

Suy ra biến cố đối của biến cố E là : “Trong 3 quyển sách được lấy ra không có quyển sách Toán nào”.

Lấy ngẫu nhiên 3 quyển sách trong số 5 quyển sách Vật lí và Hóa học và không tính đến thứ tự thì có $C_5^3=10$ cách chọn.

Tức là $n\left(\overline{E}\right)=10$.

Khi đó xác suất của biến cố $\overline{E}$ là: $P\left(\overline{E}\right)=\frac{n\left(\overline{E}\right)}{n\left(\Omega \right)}=\frac{10}{84}=\frac{5}{42}$.

Ta có $P\left(E\right)+P\left(\overline{E}\right)=1$.

Suy ra $P\left(E\right)=1-P\left(\overline{E}\right)=1-\frac{5}{42}=\frac{37}{42}$.

Vậy ta chọn phương án D.

Câu 9. Chọn ngẫu nhiên một số tự nhiên có 4 chữ số khác nhau. Gọi A là biến cố “Số tự nhiên được chọn gồm 4 số 3; 4; 5; 6”. Xác suất của biến cố A là:

A. $\frac{1}{189}$;               

B. $\frac{4}{21}$;                 

C. $\frac{1}{504}$;               

D. $\frac{2}{63}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

+) Gọi số tự nhiên gồm 4 chữ số khác nhau là $\overline{abcd}$.

Có tất có 10 chữ số là {0; 1; 2; …; 9}.

• Chọn a có 9 cách chọn từ các chữ số trong {1; 2; …; 8; 9}.

• Chọn 3 chữ số còn lại trong 9 chữ số và xếp vào 3 vị trí b, c, d có $A_9^3$ cách.

Do đó chọn ngẫu nhiên một số tự nhiên có 4 chữ số khác nhau (có quan tâm đến thứ tự) thì có $9A_9^3$ = 4 536 cách chọn.

Tức là ta có số phần tử của không gian mẫu n(Ω) = 4 536.

+) Số tự nhiên được chọn gồm 4 số 3; 4; 5; 6.

• Chọn a có 4 cách chọn từ các chữ số trong {3; 4; 5; 6}.

• Chọn b có 3 cách chọn một chữ số từ ba chữ số còn lại sau khi chọn a.

• Chọn c có 2 cách chọn một chữ số từ ba chữ số còn lại sau khi chọn a, b.

• Chọn d có 1 cách chọn một chữ số còn lại sau khi chọn a, b, c.

Số phần tử của A là: n(A) = 4.3.2 = 24.

Hoặc ta cũng có thể tính n(A) như sau:

Chọn 4 chữ số trong tập hợp các chữ số {3; 4; 5; 6} và xếp vào 4 vị trí a, b, c, d sẽ có 4! = 24 cách.

Xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{24}{4536}=\frac{1}{189}$.

Vậy ta chọn phương án A.

Câu 10. Một tổ có 9 học sinh, trong đó có 5 học sinh nam và 4 học sinh nữ được xếp thành hàng dọc. Xác suất sao cho 5 học sinh nam đứng kề nhau là:

A. $\frac{5}{126}$;               

B. $\frac{121}{126}$;                

C. $\frac{1}{126}$;                

D. $\frac{6}{125}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

Một tổ có 9 học sinh được xếp thành hàng dọc.

Suy ra số phần tử của không gian mẫu là: n(Ω) = 9!.

Gọi biến cố A: “5 học sinh nam đứng kề nhau”.

• Xếp 5 học sinh nam đứng kề nhau thì sẽ có 5! cách xếp.

• Sau đó ta coi 5 học sinh nam là 1 “người A”, rồi xếp “người A” cùng với 4 bạn nữ kia, tức là xếp 5 người, ta lại có 5! cách xếp.

Vì vậy n(A) = 5!.5!.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{5!.5!}{9!}=\frac{5}{126}$.

Ta chọn phương án A.

III. Vận dụng

Câu 1. Có năm đoạn thẳng có độ dài lần lượt là 1 cm, 3 cm, 5 cm, 7 cm và 9 cm. Chọn ngẫu nhiên ba đoạn thẳng trong số năm đoạn thẳng trên. Xác suất để ba đoạn thẳng được chọn lập thành một tam giác là:

A. $\frac{7}{10}$;                 

B. $\frac{3}{5}$;         

C. $\frac{3}{10}$;                 

D. $\frac{2}{5}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

Chọn ngẫu nhiên ba đoạn thẳng trong số năm đoạn thẳng và không tính đến thứ tự thì có $C_5^3=10$ cách chọn.

Suy ra số phần tử của không gian mẫu là: n(Ω) = 10.

Gọi biến cố S: “Ba đoạn thẳng được chọn lập thành một tam giác”.

Theo bất đẳng thức tam giác, ta có trong một tam giác, tổng độ dài hai cạnh bất kì luôn lớn hơn độ dài cạnh còn lại.

Trong năm đoạn thẳng trên, ta thấy các đoạn thẳng sau lập thành một tam giác:

⦁ 3 cm; 5 cm và 7 cm;

⦁ 3 cm; 7 cm và 9 cm;

⦁ 5 cm; 7 cm và 9 cm.

Suy ra biến cố S có ba kết quả thuận lợi hay n(S) = 3.

Vậy xác suất của biến cố S là: $\frac{3}{10}$.

Ta chọn phương án C.

Câu 2. Một hộp quà đựng 16 dây buộc tóc cùng chất liệu, cùng kiểu dáng nhưng khác nhau về màu sắc. Trong hộp có 8 dây xanh, 5 dây đỏ, 3 dây vàng. Bạn Hoa được chọn ngẫu nhiên 6 dây từ hộp quà để làm phần thưởng cho mình. Xác suất để trong 6 dây bạn Hoa chọn có ít nhất 1 dây vàng và có không quá 4 dây đỏ là:

A. $\frac{571}{728}$;               

B. $\frac{11}{14}$;                 

C. $\frac{6289}{8008}$;             

D. $\frac{1719}{8008}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

Chọn ngẫu nhiên 6 dây trong số 16 dây và không tính đến thứ tự thì có $C_{16}^6=8008$ cách chọn.

Suy ra số phần tử của không gian mẫu là: n(Ω) = 8 008.

Gọi A: “Trong 6 dây bạn Hoa chọn có ít nhất 1 dây vàng và có không quá 4 dây đỏ”.

Suy ra biến cố đối của biến cố A là $\overline{A}$: “Trong 6 dây bạn Hoa chọn không có dây vàng hoặc có hơn 4 dây đỏ”.

Các trường hợp của biến cố đối $\overline{A}$ là:

⦁ Trường hợp 1: Không có dây vàng nào. Có 8 + 5 = 13 dây xanh và đỏ.

Khi đó Hoa có $C_{13}^6$ cách chọn 6 dây trong 13 dây đó.

⦁ Trường hợp 2: Có 1 dây vàng và 5 dây đỏ.

Khi đó Hoa có $C_3^1.C_5^5$ cách chọn 1 dây vàng (trong 3 dây vàng) và 5 dây đỏ (trong 5 dây đỏ).

⦁ Trường hợp 3: Có 1 dây xanh và 5 dây đỏ.

Khi đó ta có $C_8^1.C_5^5$ cách chọn 1 dây xanh (trong 8 dây xanh) và 5 dây đỏ (trong 5 dây đỏ).

Kết hợp cả 3 trường hợp, ta có:

$n\left(\overline{A}\right)=C_{13}^6+C_3^1.C_5^5+C_8^1.C_5^5=1727$.

Suy ra xác suất của biến cố $P\left(A\right)+P\left(\overline{A}\right)=1$ là:

$P\left(A\right)=1-P\left(\overline{A}\right)=1-\frac{157}{728}=\frac{571}{728}$.

Ta có $P\left(A\right)+P\left(\overline{A}\right)=1$.

Suy ra $P\left(A\right)=1-P\left(\overline{A}\right)=1-\frac{157}{728}=\frac{571}{728}$.

Vậy ta chọn phương án A.

Câu 3. Một hộp chứa 3 viên bi xanh, 5 viên bi đỏ và 6 viên bi vàng. Lấy ngẫu nhiên 6 viên bi từ hộp. Xác suất để 6 viên bi được lấy ra có đủ cả 3 màu là:

A. $\frac{810}{1001}$;             

B. $\frac{191}{1001}$;             

C. $\frac{4}{21}$;                 

D. $\frac{17}{21}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

Có tất cả 3 + 5 + 6 = 14 viên bi.

Chọn ngẫu nhiên 6 viên bi trong số 14 viên bi trong hộp và không tính đến thứ tự thì có $C_{14}^6=3003$ cách chọn.

Suy ra số phần tử của không gian mẫu là: n(Ω) = 3 003.

Gọi A: “6 viên bi được lấy ra có đủ cả 3 màu”.

Suy ra $\overline{A}$: “6 viên bi được lấy ra không có đủ 3 màu”.

Các trường hợp của biến cố $\overline{A}$ là:

⦁ Trường hợp 1: Chọn ra 6 viên bi chỉ có một màu.

Suy ra chỉ chọn được cả 6 viên màu vàng.

Do đó ta có 1 cách chọn.

⦁ Trường hợp 2: Chọn 6 viên bi có hai màu xanh và đỏ. Có 3 + 5 = 8 viên bi màu xanh, đỏ.

Khi đó ta có $C_8^6$ cách chọn.

⦁ Trường hợp 3: Chọn 6 viên bi có hai màu xanh và vàng. Có 3 + 6 = 9 viên bi màu xanh, vàng.

Khi đó ta có $C_9^6-1$ cách chọn (ta trừ đi 1 tức là trừ đi trường hợp chọn được cả 6 viên bi đều màu vàng).

⦁ Trường hợp 4: Chọn 6 viên bi có hai màu đỏ và vàng. Có 5 + 6 = 11 viên bi màu đỏ, vàng.

Khi đó ta có $C_{11}^6-1$ cách chọn (ta trừ đi 1 tức là trừ đi trường hợp chọn được cả 6 viên bi đều màu vàng).

Suy ra số phần tử của biến cố $\overline{A}$ là:

$n\left(\overline{A}\right)=1+C_8^6+C_9^6-1+C_{11}^6-1=573$.

Khi đó xác suất của biến cố $\overline{A}$ là:

$P\left(\overline{A}\right)=\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{573}{3003}=\frac{191}{1001}$.

Ta có $P\left(A\right)+P\left(\overline{A}\right)=1$.

Suy ra $P\left(A\right)=1-P\left(\overline{A}\right)=1-\frac{191}{1001}=\frac{810}{1001}$.

Vậy ta chọn phương án A.

Câu 4. Trong một buổi liên hoan có 10 cặp nam nữ, trong đó có 4 cặp vợ chồng. Chọn ngẫu nhiên 3 người để biểu diễn một tiết mục văn nghệ. Xác suất để 3 người được chọn không có cặp vợ chồng nào là:

A. $\frac{94}{95}$;                 

B. $\frac{1}{95}$;                  

C. $\frac{6}{95}$;                 

D. $\frac{89}{95}$.

Hướng dẫn giải

Đáp án: D

Giải thích:

Số cách chọn ngẫu nhiên 3 người trong số 20 người là: $C_{20}^3=1140$.

Suy ra n(Ω) = 1 140.

Gọi A: “Trong 3 người được chọn không có cặp vợ chồng nào”.

Suy ra $\overline{A}$: “Trong 3 người được chọn có 1 cặp vợ chồng”.

Chọn 1 cặp vợ chồng trong số 4 cặp vợ chồng có $C_4^1$ cách chọn.

Chọn thêm 1 người trong số 18 người còn lại có $C_{18}^1$ cách chọn.

Suy ra $n\left(\overline{A}\right)=C_4^1.C_{18}^1=72$.

Xác suất của biến cố $\overline{A}$ là:

$P\left(\overline{A}\right)=\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{72}{1140}=\frac{6}{95}$.

Ta có $P\left(A\right)+P\left(\overline{A}\right)=1$.

Suy ra $P\left(A\right)=1-P\left(\overline{A}\right)=1-\frac{6}{95}=\frac{89}{95}$.

Vậy ta chọn phương án D.

Câu 5. Trong buổi sinh hoạt nhóm của lớp, tổ một có 12 học sinh gồm 4 học sinh nữ trong đó có Mai và 8 học sinh nam trong đó có Đức. Chia tổ thành 3 nhóm, mỗi nhóm gồm 4 học sinh và phải có ít nhất 1 học sinh nữ. Số kết quả thuận lợi cho biến cố A: “Mai và Đức cùng một nhóm” là:

A. 2 100;

B. 1 470;

C. 840;

D. 42.

Hướng dẫn giải

Đáp án: B

Giải thích:

Xét biến cố A: “Mai và Đức cùng một nhóm”, ta mô tả các khả năng thuận lợi cho biến cố A như sau:

Trường hợp 1:

• Mai và Đức cùng với 1 bạn nam và 1 bạn nữ thành một nhóm nên có duy nhất 1 cách chọn Mai và Đức và có  cách chọn 1 bạn nam (trong 7 bạn nam còn lại) và 1 bạn nữ (trong 3 bạn nữ còn lại).

• Nhóm thứ hai có 3 bạn nam (trong 6 bạn nam còn lại) và 1 bạn nữ (trong 2 bạn nữ còn lại) nên có $C_6^3.C_2^1$ cách.

• Cuối cùng còn lại 3 bạn nam và 1 bạn nữ nên có 1 cách duy nhất cho nhóm thứ ba.

Do đó trong trường hợp này có $1.C_3^1.C_7^1.C_6^3.C_2^1.1=840$ cách.

Trường hợp 2:

• Mai và Đức cùng với 2 bạn nam thành một nhóm nên có duy nhất 1 cách chọn Mai và Đức và có $C_7^2$ cách chọn 2 bạn nam trong 7 bạn nam còn lại.

• Nhóm thứ hai có 2 bạn nam (trong 5 bạn nam còn lại) và 1 bạn nữ (trong 3 bạn nữ còn lại) nên có $C_5^2.C_3^1$ cách.

• Cuối cùng còn lại 2 bạn nam và 2 bạn nữ nên có 1 cách duy nhất cho nhóm thứ ba.

Do đó trong trường hợp này có $1.C_7^2.C_5^2.C_3^1.1=630$ cách.

Trường hợp 3:

• Mai và Đức cùng với 2 bạn nam thành một nhóm.

• Nhóm thứ hai có 2 bạn nam và 2 bạn nữ.

• Suy ra nhóm thứ ba có 3 bạn nam và 1 bạn nữ.

Trường hợp này trùng với trường hợp thứ hai nên ta không tính.

Suy ra số kết quả thuận lợi cho biến cố A là 840 + 630 = 1 470.

Câu 6. Xếp ngẫu nhiên 10 học sinh gồm 5 học sinh nam (trong đó có Bình) và 5 học sinh nữ (trong đó có Phương) thành một hàng ngang. Số kết quả thuận lợi cho biến cố A: “Trong 10 học sinh trên không có hai học sinh cùng giới đứng cạnh nhau, đồng thời Bình và Phương cũng không đứng cạnh nhau” là:

A. 4 608;

B. 9 216;

C. 13 824;

D. 18 432.

Hướng dẫn giải

Đáp án: D

Giải thích:

Chọn vị trí chẵn hoặc lẻ để xếp 5 nam: có 2 cách.

Ta xét trường hợp 5 nam ở vị trí chẵn (tương tự cho vị trí lẻ):

• Khả năng 1: Bình đứng ngoài cùng: có 1 cách.

Xếp Phương không cạnh Bình: có 4 cách.

Đổi vị trí các bạn nam: có 4! cách;

Đổi vị trí các bạn nữ: 4! cách.

Do đó trong khả năng này có 2.1.4.4!.4! = 4 608 cách.

• Khả năng 2: Bình không đứng ngoài cùng: có 4 cách.

Xếp Phương không cạnh Bình (bỏ 2 vị trí cạnh Bình): có 3 cách.

Đổi vị trí các bạn nam: có 4! cách;

Đổi vị trí các bạn nữ: có 4! cách.

Do đó trong khả năng này có 2.4.3.4!4! = 13 824 cách.

Khi đó có 4 608 + 13 824 = 18 432 cách.

Vậy số kết quả thuận lợi cho biến cố A là 18 432.

Câu 7. Có 4 hành khách bước lên một đoàn tàu gồm 4 toa. Mỗi hành khách độc lập với nhau và chọn ngẫu nhiên một toa. Xác suất để 1 toa có 3 người, 1 toa có 1 người và 2 toa còn lại không có ai là:

A. $\frac{3}{4}$;         

B. $\frac{3}{4}$;                 

C. $\frac{13}{16}$;                 

D. $\frac{1}{4}$.

Hướng dẫn giải

Đáp án: B

Giải thích:

Không gian mẫu của phép thử trên là số cách xếp 4 hành khách lên 4 toa tàu.

Vì chọn mỗi hành khách có 4 cách chọn toa nên ta có 4⁴ cách xếp.

Suy ra số phần tử của không gian mẫu là n(Ω) = 4⁴.

Gọi biến cố A: “1 toa có 3 người, 1 toa có 1 người và 2 toa còn lại không có ai”.

Để tìm số phần tử của biến cố A, ta chia thành hai giai đoạn như sau:

Giai đoạn 1: Chọn 3 hành khách trong số 4 hành khách và chọn 1 toa trong số 4 toa.

Sau đó xếp lên toa đó 3 hành khách vừa chọn.

Khi đó ta có $C_4^3.C_4^1$ cách.

Giai đoạn 2: Chọn 1 toa trong số 3 toa còn lại và xếp 1 hành khách còn lại lên toa đó.

Suy ra có $C_3^1$ cách. Hiển nhiên khi đó 2 toa còn lại sẽ không có hành khách nào.

Theo quy tắc nhân, ta có n(A) = $C_4^3.C_4^1.C_3^1$.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{C_4^3.C_4^1.C_3^1}{4^4}=\frac{3}{16}$.

Ta chọn phương án B.

Câu 8. Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có tọa độ các đỉnh A(–2; 0), B(–2; 2), C(4; 2), D(4; 0). Chọn ngẫu nhiên một điểm có tọa độ (x; y) (với x, y là các số nguyên) nằm trong hình chữ nhật ABCD, kể cả các điểm nằm trên cạnh. Gọi A là biến cố “x, y đều chia hết cho 2”. Xác suất của biến cố A là:

A. $\frac{7}{21}$;                 

B. $\frac{13}{21}$;                 

C. 1;           

D. $\frac{8}{21}$.

Hướng dẫn giải

Đáp án: D

Giải thích:

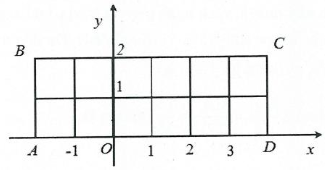
Ta có Ω = {(x; y) | x, y ∈ ℤ; –2 ≤ x ≤ 4 và 0 ≤ y ≤ 2}.

Khi đó x ∈ {–2; –1; 0; 1; 2; 3; 4} và y ∈ {0; 1; 2}.

Chọn 1 hoành độ có 7 cách chọn và chọn 1 tung độ có 3 cách chọn.

Áp dụng quy tắc nhân, ta suy ra n(Ω) = 7.3 = 21 (mỗi điểm là một giao điểm trên hình).

Ta có A: “x, y đều chia hết cho 2”.

Suy ra A = {(x; y) | x ∈ {–2; 0; 2; 4} và y ∈ {0; 2}}.

Chọn 1 hoành độ (chia hết cho 2) có 4 cách chọn và chọn 1 tung độ (chia hết cho 2) thì có 2 cách chọn.

Theo quy tắc nhân, ta có n(A) = 4.2 = 8.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{8}{21}$.

Ta chọn phương án D.

Câu 9. Gieo một con xúc xắc cân đối và đồng chất. Giả sử xúc xắc xuất hiện mặt b chấm. Xác suất để phương trình x² + bx + 2 = 0 có hai nghiệm phân biệt là:

A. $\frac{2}{3}$;         

B. $\frac{5}{6}$;         

C. $\frac{1}{3}$;         

D. $\frac{1}{2}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

Số phần tử của không gian mẫu là: n(Ω) = 6.

Gọi K: “Phương trình x² + bx + 2 = 0 có hai nghiệm phân biệt”.

Ta có ∆ = b² – 8.

Phương trình x² + bx + 2 = 0 có hai nghiệm phân biệt khi và chỉ khi ∆ > 0

⇔ b² – 8 > 0

$\iff \left[\begin{array}{l}b<-2\sqrt{2}\\ b>2\sqrt{2}\end{array}\right.$

Lại có xúc xắc xuất hiện mặt b chấm nên b ∈ {1; 2; 3; 4; 5; 6}.

Do đó ta nhận b ∈ {3; 4; 5; 6}.

Suy ra n(K) = 4.

Vậy xác suất của biến cố K là: $P\left(K\right)=\frac{n\left(K\right)}{n\left(\Omega \right)}=\frac{4}{6}=\frac{2}{3}$.

Ta chọn phương án A.

Câu 10. Gieo một con xúc xắc cân đối và đồng chất. Giả sử con xúc xắc xuất hiện mặt b chấm. Xác suất sao cho phương trình x² – bx + b – 1 = 0 (x là ẩn số) có nghiệm lớn hơn 3 là:

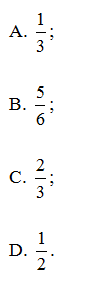
Hướng dẫn giải

Đáp án: A

Giải thích:

Số phần tử của không gian mẫu là: n(Ω) = 6.

Gọi H: “Phương trình x² – bx + b – 1 = 0 có nghiệm lớn hơn 3”.

Ta có xúc xắc xuất hiện mặt b chấm.

Suy ra b ∈ {1; 2; 3; 4; 5; 6}.

Xét phương trình x² – bx + b – 1 = 0  (1)

∆ = (–b)² – 4.1.(b – 1) = b² – 4b + 4 = (b – 2)² ≥ 0, với mọi b ∈ ℝ.

Suy ra phương trình đã cho có hai nghiệm x₁, x₂ là:

$x_1=\frac{b+b-2}{2}=b-1;x_2=\frac{b-b+2}{2}=1$

Theo đề, ta có phương trình đã cho có nghiệm lớn hơn 3.

Mà x₂ = 1 < 3

Suy ra x₁ > 3

⇔ b – 1 > 3

⇔ b > 4.

Mà b ∈ {1; 2; 3; 4; 5; 6} và 2 ≤ b ≤ 6.

Suy ra ta nhận b = 5 và b = 6.

Khi đó số phần tử của tập hợp mô tả biến cố H là: n(H) = 2.

Xác suất của biến cố H là: $P\left(H\right)=\frac{n\left(H\right)}{n\left(\Omega \right)}=\frac{2}{6}=\frac{1}{3}$.

Vậy ta chọn phương án A.

Xem thêm các bài trắc nghiệm Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Toán 10 Bài 3: Đường tròn trong mặt phẳng toạ độ

Trắc nghiệm Toán 10 Bài 4: Ba đường conic trong mặt phẳng toạ độ

Trắc nghiệm Ôn tập chương 9

Trắc nghiệm Bài 1. Không gian mẫu và biến cố

Trắc nghiệm Bài 2. Xác suất của biến cố

Trắc nghiệm Ôn tập chương 10