Lý thuyết Dấu của tam thức bậc hai (Chân trời sáng tạo 2023) hay, chi tiết | Toán lớp 10

Lý thuyết Toán lớp 10 Bài 1: Dấu của tam thức bậc hai

A. Lý thuyết Dấu của tam thức bậc hai

1. Tam thức bậc hai

– Đa thức bậc hai f(x) = ax² + bx + c với a, b, c là các hệ số, a ≠ 0 và x là biến số được gọi là tam thức bậc hai.

Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0). Khi thay x bằng giá trị x₀ vào f(x), ta được  gọi là giá trị của tam thức bậc hai  tại x₀.

• Nếu f(x₀) > 0 thì ta nói f(x) dương tại x₀.

• Nếu f(x₀) < 0 thì ta nói f(x) âm tại x₀.

• Nếu f(x) dương (âm) tại mọi điểm x thuộc một khoảng hoặc một đoạn thì ta nói f(x) dương (âm) trên khoảng hoặc đoạn đó.

Ví dụ: Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại x = 3.

a) f(x) = x² + 2x⁴ – 2;

b) f(x) = –x² + 2x – 3;

c) f(x) = 3x² – $\sqrt{5}$x.

Hướng dẫn giải

a) Biểu thức f(x) = x² + 2x⁴ – 2 không phải là tam thức bậc hai vì có chứa x⁴.

b) Biểu thức f(x) = –x² + 2x – 3 là tam thức bậc hai với a = –1, b = 2 và c = –3.

Khi x = 3 ta có:

f(3) = –3² + 2.3 – 3 = = –9 + 6 – 3 = –6 < 0.

Do đó f(x) âm tại x = 3.

c) Biểu thức f(x) = 3x² – $\sqrt{5}$x là tam thức bậc hai với a = 3, b = $–\sqrt{5}$  và c = 0.

Khi x = 3 ta có:

f(3) = 3.3² – $\sqrt{5}$.3 = 27 – 3$\sqrt{5}$ > 0

Do đó f(x) dương tại x = 3.

– Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0). Khi đó:

• Nghiệm của phương trình bậc hai ax² + bx + c là nghiệm của f(x).

• Biểu thức ∆ = b² – 4ac và ${\Delta }^{‘}={\left(\frac{b}{2}\right)}^2-ac$ lần lượt là biệt thức và biệt thức rút gọn của f(x).

Ví dụ: Tìm biệt thức (hoặc biệt thức thu gọn) và nghiệm (nếu có) của các tam thức bậc hai sau:

a) f(x) = x² + 2x – 5;

b) f(x) = = –3x² + 18x – 27;

c) f(x) = x + x² + 1.

Hướng dẫn giải

a) f(x) = x² + 2x – 5 có ∆’ = 1² – 1.(–5) = 6 > 0.

Do đó f(x) có hai nghiệm phân biệt là:

$x_1=-1+\sqrt{6}$ và  $x_2=-1-\sqrt{6}$

Vậy tam thức bậc hai đã cho có hai nghiệm là $x_1=-1+\sqrt{6}$  và $x_2=-1-\sqrt{6}$  

b) f(x) = –3x² + 18x – 27

f(x) có ∆’ = 9² – (‒3).(–27) = 0

Do đó f(x) có nghiệm kép là $x=\frac{-9}{-3}=3$  

Vậy tam thức bậc hai đã cho có nghiệm là x = 3.

c) f(x) = x + x² + 1 = x² + x + 1.

f(x) có ∆ = 1² – 4.1.1 = –3 < 0.

Do đó f(x) vô nghiệm.

Vậy tam thức bậc hai đã cho vô nghiệm.

2. Định lí về dấu của tam thức bậc hai

Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0).

+  Nếu ∆ < 0 thì f(x) cùng dấu với a với mọi giá trị x.

+ Nếu ∆ = 0 và $x_0=-\frac{b}{2a}$ là nghiệm kép của f(x) thì f(x) cùng dấu với a với mọi x khác x₀.

+ Nếu ∆ > 0 và x₁, x₂ là hai nghiệm của f(x) (x₁ < x₂) thì:

• f(x) trái dấu với a với mọi x trong khoảng (x₁; x₂);

• f(x) cùng dấu với a với mọi x thuộc hai khoảng (–∞; x₁), (x₂; +∞).

Chú ý:

+ Để xét dấu tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0), ta thực hiện các bước sau:

Bước 1: Tính và xác định dấu của biệt thức ∆;

Bước 2: Xác định nghiệm của f(x) (nếu có);

Bước 3: Xác định dấu của hệ số a;

Bước 4: Xác định dấu của f(x).

+ Khi xét dấu của tam thức bậc hai, ta có thể dùng biệt thức thu gọn ∆’ thay cho biệt thức ∆.

Ví dụ: Xét dấu của các tam thức bậc hai sau:

a) f(x) = 3x² + 6x – 9;

b) f(x) = –2x² + 8x + 10;

c) f(x) = 4x² + 8x + 4;

d) f(x) = –3x² + 2x – 1.

Hướng dẫn giải

a) f(x) = 3x² + 6x – 9

f(x) có a = 3 > 0 và ∆’ = 3² – 3.(–9) = 36 > 0.

Khi đó f(x) có hai nghiệm phân biệt là:

$x_1=\frac{-3+\sqrt{36}}{3}=1$ và  $x_1=\frac{-3–\sqrt{36}}{3}=–3$

Ta có bảng xét dấu của f(x) như sau:

x	–∞		–3		1		+∞
f(x)		+	0	–	0	+

Vậy, f(x) dương trong khoảng (–∞; –3) và (1; +∞);

f(x) âm trong khoảng (–3; 1).

b) f(x) = –2x² + 8x + 10

f(x) có a = –2 < 0 và ∆’ = 4² – (–2).10 = 36 > 0.

Khi đó f(x) có hai nghiệm phân biệt là:

$x_1=\frac{-4+\sqrt{36}}{-2}=-1$ và  $x_2=\frac{-4-\sqrt{36}}{-2}=5$

Ta có bảng xét dấu của f(x) như sau:

x	–∞		–1		5		+∞
f(x)		–	0	+	0	–

Vậy, f(x) âm trong khoảng (–∞; –1) và (5; +∞);

f(x) dương trong khoảng (–1; 5).

c) f(x) = 4x² + 8x + 4

f(x) có a = 4 > 0 và ∆’ = 4² – 4.4 = 0.

Khi đó f(x) có nghiệm kép là $x=\frac{-4}{4}=-1$   

Vậy, f(x) dương với mọi x ≠ –1.

d) f(x) = –3x² + 2x – 1.

f(x) có a = –3 < 0 và ∆’ = 1² – (–3).(–1) = –2 < 0.

Vậy f(x) âm với mọi x ∈ ℝ.

B. Bài tập tự luyện

Bài 1. Cho các đa thức sau, những đa thức nào là tam thức bậc hai? Nếu là tam thức bậc hai hãy xét dấu của tam thức bậc hai đó.

a) $f\left(x\right)=\sqrt{2}{x}^2-\left(\sqrt{2}+1\right)x+1;$

b) f(x) = x³ – x² + 1;

c) f(x) = –2x² – 2x – 5;

d) $f\left(x\right)=\sqrt{3}{x}^2-x^3+\left(1-\sqrt{3}\right)x^4;$

e) f(x) = –x² + 4x – 3.

Hướng dẫn giải

a) $f\left(x\right)=\sqrt{2}{x}^2-\left(\sqrt{2}+1\right)x+1$

f(x) là tam thức bậc hai có a = $\sqrt{2}>0,$b =$-\left(\sqrt{2}+1\right),$ c = 1

Ta có ∆ =${\left[-\left(\sqrt{2}+1\right)\right]}^2-4.\sqrt{2}.1$

∆ = 2 + 2$\sqrt{2}$  + 1 – 4$\sqrt{2}$  

∆ = 2 – 2$\sqrt{2}$  + 1 =${\left(\sqrt{2}-1\right)}^2$  > 0.

$\Rightarrow \sqrt{\Delta }=\sqrt{2}-1$ 

Khi đó f(x) có hai nghiệm phân biệt là:

$x_1=\frac{\sqrt{2}+1+\sqrt{2}-1}{2.\sqrt{2}}=1$ và  $x_2=\frac{\sqrt{2}+1-\sqrt{2}+1}{2.\sqrt{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}.$

Ta có bảng xét dấu của f(x) như sau:

x	–∞		$\frac{\sqrt{2}}{2}$		1		+∞
f(x)		+	0	–	0	+

Vậy, f(x) dương trong khoảng $\left(-\infty ;\frac{\sqrt{2}}{2}\right)$ và (1; +∞);

f(x) âm trong khoảng $\left(\frac{\sqrt{2}}{2};1\right).$  

b) f(x) = x³ – x² + 1

f(x) không phải là tam thức bậc hai vì có chứa x³.

c) f(x) = –2x² – 2x – 5

f(x) là tam thức bậc hai có a = –2 < 0, b = –2, c = –5.

Ta có ∆’ = (–1)² – (–2).(–5) = –9 < 0.

Vậy f(x) luôn âm với mọi x ∈ ℝ.

d) $f\left(x\right)=\sqrt{3}{x}^2-x^3+\left(1-\sqrt{3}\right)x^4;$

f(x) không phải là tam thức bậc hai vì có chứa x⁴ và x³.

e) f(x) = –x² + 4x – 3

f(x) là tam thức bậc hai có a = –1 < 0, b = 4, c = –3.

Ta có: ∆’ = 2² – (–1).(–3) = 1 > 0

Khi đó f(x) có hai nghiệm phân biệt là:

$x_1=\frac{-2+\sqrt{1}}{-1}=1$  và  $x_2=\frac{-2-\sqrt{1}}{-1}=3$

Ta có bảng xét dấu của f(x) như sau:

x	–∞		1		3		+∞
f(x)		–	0	+	0	–

Vậy, f(x) âm trong khoảng (–∞; 1) và (3; +∞); f(x) dương trong khoảng (1; 3).

Bài 2. Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng.

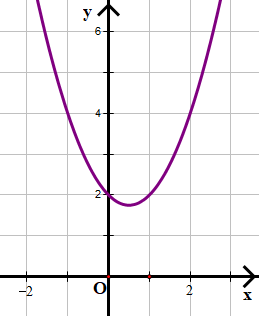
a) f(x) = x² – x + 2      

            

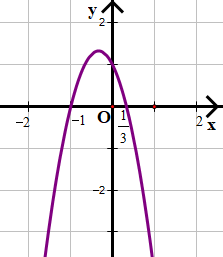
b) f(x) = –3x² – 2x + 1

                   

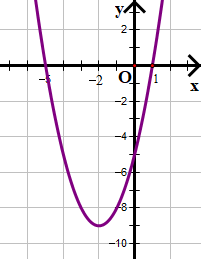
c) f(x) = x² + 4x – 5

                           

d) 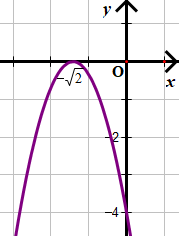$f\left(x\right)=-2x^2-4\sqrt{2}x-4$                    

Hướng dẫn giải

a) f(x) = x² – x + 2

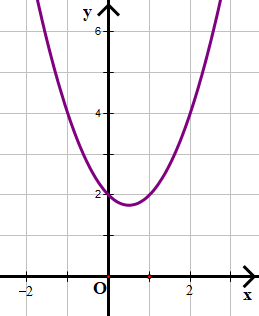
Quan sát hình vẽ ta thấy đồ thị hàm số f(x) nằm hoàn toàn ở trên (không cắt) trục hoành.

Do đó f(x) vô nghiệm và f(x) > 0 với mọi x.

Ta có bảng xét dấu của f(x) như sau:

x	–∞		+∞
f(x)		+

b) f(x) = –3x² – 2x + 1

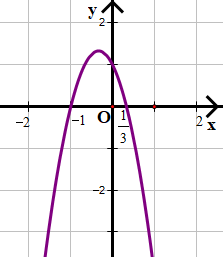
Quan sát hình vẽ ta thấy:

• Với x trong khoảng (–∞; –1) và $\left(\frac{1}{3};+\infty \right)$  ta thấy đồ thị nằm bên dưới trục hoành

$\Rightarrow$ f(x) < 0 trong khoảng (–∞; –1) và $\left(\frac{1}{3};+\infty \right)$

• Với x trong khoảng $\left(1;\frac{1}{3}\right)$ ta thấy đồ thị nằm bên trên trục hoành

$\Rightarrow$ f(x) > 0 trong khoảng $\left(1;\frac{1}{3}\right).$

Ta có bảng xét dấu của f(x) như sau:

x	–∞		1		$\frac{1}{3}$		+∞
f(x)		–	0	+	0	–

c) f(x) = x² + 4x – 5

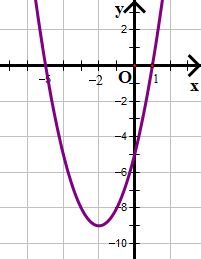
Quan sát hình vẽ ta thấy:

• Với x trong khoảng (–∞; –5) và (1; +∞) ta thấy đồ thị nằm bên trên trục hoành

$\Rightarrow$Þ f(x) > 0 trong khoảng (–∞; –5) và (1; +∞).

• Với x trong khoảng (–5; 1) ta thấy đồ thị nằm bên dưới trục hoành

$\Rightarrow$ f(x) < 0 trong khoảng (–5; 1).

Ta có bảng xét dấu của f(x) như sau:

x	–∞		–5		1		+∞
f(x)		+	0	–	0	+

d) $f\left(x\right)=-2x^2-4\sqrt{2}x-4$

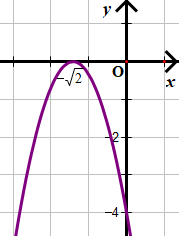
Quan sát hình vẽ ta thấy:

• Với x trong khoảng $\left(-\infty ;-\sqrt{2}\right)$ và $\left(-\sqrt{2};+\infty \right)$ ta thấy đồ thị nằm bên dưới trục hoành

$\Rightarrow$ f(x) < 0 trong khoảng $\left(-\infty ;-\sqrt{2}\right)$ và $\left(-\sqrt{2};+\infty \right).$

Ta có bảng xét dấu của f(x) như sau:

x	–∞				+∞
f(x)		–	0	–

Bài 8. Tổng chi phí để sản xuất x sản phẩm được cho bởi biểu thức x² + 202x + 12 500 (nghìn đồng); giá bán của một sản phẩm là 500 nghìn đồng. Số sản phẩm sản xuất phải trong khoảng nào thì bị lỗ, trong khoảng nào thì có lãi?

Hướng dẫn giải

Vì giá bán một sản phẩm là 500 nghìn đồng nên với x sản phẩm thì có doanh thu là 500x (nghìn đồng).

Do tổng chi phí để sản xuất ra x sản phầm là x² + 202x + 12 500 (nghìn đồng) nên lợi nhuận thu về từ x sản phẩm là:

500x – (x² + 202x + 12 500)

= – x² + 298x – 12 500.

Đặt f(x) = –x² + 298x – 12 500.

Ta có: ∆’ = 149² – (–1)(–12 500) = 9 701 > 0.

Khi đó f(x) có hai nghiệm phân biệt là:

$x_1=\frac{-149+\sqrt{9701}}{-1}\approx 50,5$ và $x_2=\frac{-149-\sqrt{9701}}{-1}\approx 247,5$ .

Mặt khác a = –1 < 0 nên ta có bảng xét dấu sau:

x	– ∞	50,5		247,5	+ ∞
f(x)	–	0	+	0	–

Từ bảng xét dấu ta thấy f(x) > 0 khi x trong khoảng (50,5; 247,5);

f(x) < 0 khi x trong khoảng (–∞; 50,5) và (247,5; +∞).

Mặt khác, vì x là số sản phẩm nên x nguyên dương.

Do đó:

• Bị lỗ khi số sản phẩm sản xuất từ 0 đến 50 sản phẩm hoặc không nhỏ hơn 248 sản phẩm.

• Để có lãi thì số sản phẩm sản xuất phải từ 51 đến 247 sản phẩm.

Lý thuyết Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Lý thuyết Bài 1: Dấu của tam thức bậc hai

Lý thuyết Bài 2: Giải bất phương trình bậc hai một ẩn

Lý thuyết Bài 3: Phương trình quy về phương trình bậc hai

Lý thuyết Bài 1: Quy tắc cộng và quy tắc nhân