Giải SBT Toán lớp 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách
Giải SBT Toán 10 trang 37 Tập 2
Bài 7.10 trang 37 SBT Toán 10 Tập 2: Xét vị trí tương đối của các cặp đường thẳng sau:
a) m: x + y – 2 = 0 và k: 2x + 2y – 4 = 0.
b) và .
c) d1: x – 2y – 1 = 0 và .
Lời giải:
a)
Xét m: x + y – 2 = 0 và k: 2x + 2y – 4 = 0 ta có:
a1 = 1, b1 = 1, c1 = –2
a2 = 2, b2 = 2, c2 = –4
Xét tỉ số:
Vậy m trùng với k.
b)
Xét và
Ta có:
Vectơ chỉ phương của a là: = (2; 0)
Vectơ chỉ phương của b là: = (3; 1)
Do nên và không cùng phương
Vậy a và b cắt nhau.
c)
Xét d1: x – 2y – 1 = 0 và
Vectơ pháp tuyến của d1 là:
Vectơ chỉ phương của d2 là: . Do đó, d2 có một vectơ pháp tuyến là:
Ta có: nên d1 và d2 song song hoặc trùng nhau
Xét d1: x – 2y – 1 = 0 . Khi x = 3 thì y = 1, do đó, điểm (3; 1) thuộc đường thẳng d1.
Xét có: (không thể tồn tại), do đó, điểm (3; 1) không thuộc đường thẳng d2
Vậy d1 // d2.
Giải SBT Toán 10 trang 38 Tập 2
Bài 7.11 trang 38 SBT Toán 10 Tập 2: Tính góc giữa các cặp đường thẳng sau:
a) d: y – 1 = 0 và k: x – y + 4 = 0;
b) và b: 3x + y + 1 = 0;
c) và .
Lời giải:
a)
Gọi φ là góc giữa hai đường thẳng d và k. Từ giả thiết ta có . Do đó, theo công thức tính góc của hai đường thẳng thì
.
Vậy góc giữa hai đường thẳng là φ = 45°.
b)
Gọi φ là góc giữa hai đường thẳng a và b. Từ giả thiết ta có
nên . Do đó, theo công thức tính góc của hai đường thẳng thì
Vậy góc giữa hai đường thẳng a và b là φ = 45°.
c)
Gọi φ là góc giữa hai đường thẳng m và n. Từ giả thiết ta có . Do đó theo công thức tính góc giữa hai đường thẳng thì
Vậy góc giữa hai đường thẳng m và n là φ = 60°.
Bài 7.12 trang 38 SBT Toán 10 Tập 2: Cho hai đường thẳng d: 2x + y + 1 = 0 và k: 2x + 5y – 3 = 0.
a) Chứng minh rằng hai đường thẳng cắt nhau. Tìm giao điểm của hai đường thẳng đó.
b) Tính tang của góc giữa hai đường thẳng.
Lời giải:
a)
Xét d: 2x + y + 1 = 0 và k: 2x + 5y – 3 = 0 ta có:
a1 = 2, b1 = 1, c1 = 1
a2 = 2, b2 = 5, c2 = –3
Xét tỉ số:
Do đó, d và k cắt nhau (điều cần phải chứng minh).
Giao điểm của hai đường thẳng có tọa độ là nghiệm của hệ phương trình:
Vậy tọa độ giao điểm của hai đường thẳng là (–1; 1).
b)
Gọi φ là góc giữa hai đường thẳng d và k.
Từ giả thiết ta có
Do đó, theo công thức tính góc của hai đường thẳng thì:
Vì φ là góc giữa hai đường thẳng nên 0° ≤ φ ≤ 90°, hơn nữa cosφ ≠ 0 và cosφ ≠ 1 nên ta có: 0° < φ < 90°, suy ra tanφ > 0.
Lại có: 1 + tan2φ = .
Do đó, .
Bài 7.13 trang 38 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, tìm điểm M thuộc trục Ox sao cho khoảng cách từ M đến đường thẳng ∆: 3x + y – 3= 0 bằng .
Lời giải:
Do M thuộc Ox nên toạ độ của M có dạng M(m; 0).
Từ giả thiết ta có:
⇔ |3m – 3| = 10 (*)
TH1: 3m – 3 ≥ 0 hay m ≥ 1
Khi đó, ta có:
(*) ⇔ 3m – 3 = 10 ⇔ m = (thỏa mãn)
TH2: 3m – 3 < 0 hay m < 1
Khi đó, ta có:
(*) ⇔ –3m + 3 = 10 ⇔ m = (thỏa mãn)
Vậy có hai điểm thoả mãn là .
Bài 7.14 trang 38 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng ∆: 2x + y – 5 = 0.
a) Viết phương trình đường thẳng d qua điểm A(3; 1) và song song với đường thẳng ∆.
b) Viết phương trình đường thẳng k đi qua điểm B(–1; 0) và vuông góc với đường thẳng ∆.
c) Lập phương trình đường thẳng a song song với đường thẳng ∆ và cách điểm O một khoảng bằng .
Lời giải:
a)
Đường thẳng d qua điểm A(3; 1) và song song với đường thẳng ∆ nên nhận vectơ pháp tuyến bằng vectơ pháp tuyến của ∆ là: = (2; 1)
Phương trình đường thẳng d là:
2(x – 3) + 1(y – 1) = 0
⇔ 2x + y – 6 – 1 = 0
⇔ 2x + y – 7 = 0.
b)
Đường thẳng k đi qua điểm B(–1; 0) và vuông góc với đường thẳng ∆ nên vectơ pháp tuyến của k vuông góc với vectơ pháp tuyến của ∆. Do = (2; 1) là một vectơ pháp tuyến của ∆ nên = (1; –2) là một vectơ pháp tuyến của d.
Phương trình đường thẳng k là:
1.[x – (–1)] – 2.(y – 0) = 0
⇔ x – 2y + 1 = 0.
c)
Đường thẳng a song song với đường thẳng ∆ nên nhận vectơ pháp tuyến bằng vectơ pháp tuyến của ∆ là: = (2; 1)
Do đó, phương trình đường thẳng a có dạng: 2x + y + c = 0 với c ≠ –5.
Theo công thức tính khoảng cách ta có
⇔ |c| = 5
⇔ c = ±5
Mà c ≠ –5 nên c = 5
Vậy phương trình đường thẳng a là: 2x + y + 5 = 0.
Bài 7.15 trang 38 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho tam giác ABC có A(2; –1), B(2; –2) và C(0; –1).
a) Tính độ dài đường cao của tam giác ABC kẻ từ A.
b) Tính diện tích tam giác ABC.
c) Tính bán kính đường tròn nội tiếp tam giác ABC.
Lời giải:
a)
Độ dài đường cao của tam giác ABC kẻ từ A chính là khoảng cách từ điểm A đến cạnh BC.
Đường thẳng BC nhận là một vectơ chỉ phương. Do đó là một vectơ pháp tuyến của BC.
Đường thẳng BC đi qua đểm B(2; –2) và có một vectơ pháp tuyến là nên có phương trình tổng quát là:
1(x – 2) + 2.[y – (–2)] = 0
⇔ x + 2y – 2 + 4 = 0
⇔ x + 2y + 2 = 0
Theo công thức tính khoảng cách, ta có
Vậy độ dài đường cao của tam giác ABC kẻ từ A là: (đvđd).
b)
Ta có (đvđd)
(đvdt).
c)
(đvđd)
(đvđd)
.
Vậy bán kính đường tròn nội tiếp tam giác ABC là
(đvđd).
Bài 7.16 trang 38 SBT Toán 10 Tập 2: Cho đường thẳng d: x – 2y + 1 = 0 và điểm A(–2; 2).
a) Chứng minh A không thuộc đường thẳng d.
b) Tìm toạ độ hình chiếu vuông góc của A trên đường thẳng d.
c) Xác định điểm đối xứng của A qua đường thẳng d.
Lời giải:
a)
Thay toạ độ điểm A vào phương trình đường thẳng d ta có:
–2 – 2.2 + 1 = –5 ≠ 0
Vậy điểm A không thuộc đường thẳng d (điều cần phải chứng minh).
b)
Gọi ∆ là đường thẳng đi qua A và vuông góc với đường thẳng d. Khi đó ∆ nhận vectơ chỉ phương của đường thẳng d là một vectơ pháp tuyến nên phương trình ∆ là:
2(x + 2) + 1(y – 2) = 0
⇔ 2x + y + 4 – 2 = 0
⇔ 2x + y + 2 = 0
Hình chiếu vuông góc H của điểm A trên đường thẳng d là giao điểm của đường thẳng d và ∆. Do đó, toạ độ của điểm H là nghiệm của hệ phương trình:
Vậy H(–1; 0).
c)
Gọi A'(xA’; yA’) là điểm đối xứng với A qua d. Khi đó H là trung điểm của AA’.
Ta có:
xH = (xA + xA’) : 2 ⇔ xA’ = 2xH – xA = 2.(–1) – (–2) = 0
yH = (yA + yA’) : 2 ⇔ yA’ = 2yH – yA = 2.0 – 2 = –2
Vậy A’(0; –2).
Bài 7.17 trang 38 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho hai điểm A(–3; 0), B(1; –2) và đường thẳng d: x + y – 1 = 0.
a) Chứng minh rằng hai điểm A và B nằm cùng phía so với đường thẳng d.
b) Điểm M thay đổi trên đường thẳng d. Tìm giá trị nhỏ nhất của chu vi tam giác ABM.
Lời giải:
a)
Ta có (–3 + 0 – 1).(1 – 2 – 1) = 8 > 0 nên theo tập nghiệm của bất phương trình bậc nhất hai ẩn ta có A, B nằm cùng phía so với đường thẳng d.
b)
Dựa vào phương trình đường thẳng d ta có:
x + y – 1 = 0
⇔ y = 1 – x
Do M thuộc đường thẳng d nên toạ độ của điểm M có dạng M(t; 1– t).
Chu vi tam giác ABM là: AB + MA + MB
Mà AB luôn không đổi nên chu vi tam giác ABM nhỏ nhất khi và chỉ khi MA + MB nhỏ nhất.
Lấy A’ đối xứng với A qua đường thẳng d. Khi đó ta có:
MA + MB = MA’ + MB ≥ A’B
Dấu bằng xảy ra khi M = A’B ∩ d
Gọi H là hình chiếu vuông góc của A lên d. Khi đó AH đi qua điểm A(–3;0) và nhận vectơ chỉ phương của đường thẳng d là vectơ pháp tuyến nên phương trình của AH là:
1(x + 3) – 1(y – 0) = 0
⇔ x – y + 3 = 0
Vậy toạ độ điểm H là nghiệm của hệ phương trình
Suy ra H(–1; 2). Mặt khác, H là trung điểm của AA’ nên ta có:
xH = (xA + xA’) : 2 ⇔ xA’ = 2xH – xA = 2.(–1) – (–3) = 1
yH = (yA + yA’) : 2 ⇔ yA’ = 2yH – yA = 2.2 – 0 = 4
Do đó, ta có A’(1; 4)
Ta có là một vectơ chỉ phương của đường thẳng A’B. Do đó A’B là đường thẳng đi qua đểm A’(1; 4) và nhận là một vectơ pháp tuyến. Phương trình của đường thẳng A’B là:
1(x – 1) + 0(y – 4) = 0
⇔ x – 1 = 0
Vậy toạ độ điểm M là nghiệm của hệ phương trình
Do đó ta có M(1; 0).
Giải SBT Toán 10 trang 39 Tập 2
Bài 7.18 trang 39 SBT Toán 10 Tập 2: Trong một hoạt động ngoại khoá của trường, lớp Việt định mở một gian hàng bán bánh mì và nước khoáng. Biết rằng giá gốc một bánh mì là 15 000 đồng, một chai nước là 5 000 đồng. Các bạn dự kiến bán bánh mì với giá 20 000 đồng/1 bánh mì và nước giá 8 000 đồng/1 chai. Dựa vào thống kê số người tham gia hoạt động và nhu cầu thực tế các bạn dự kiến tổng số bánh mì và số chai nước không vượt qua 200. Theo quỹ lớp thì số tiền lớp Việt được dùng không quá 2 000 000 đồng. Hỏi lớp Việt có thể đạt được tối đa lợi nhuận là bao nhiêu ?
Lời giải:
Gọi x, y lần lượt là số chiếc bánh mì và chai nước khoáng mà lớp Việt định mua để bán. Khi đó từ giả thiết ta có: x, y ∈ ℕ.
Mặt khác từ giả thiết ta có:
Dựa vào thống kê số người tham gia hoạt động và nhu cầu thực tế các bạn dự kiến tổng số bánh mì và số chai nước không vượt qua 200 nên:
x + y ≤ 200 (1)
Biết rằng giá gốc một bánh mì là 15 000 đồng, một chai nước là 5 000 đồng. Theo quỹ lớp thì số tiền lớp Việt được dùng không quá 2 000 000 đồng nên:
15 000x + 5 000y ≤ 2 000 000 (2)
Kết hợp (1) và (2) ta có hệ bất phương trình:
Tập nghiệm của hệ bất phương trình kết hợp với điều kiện x, y ∈ ℕ được biểu diễn bởi phần tô đậm trong hình vẽ dưới đây (tứ giác OABC)
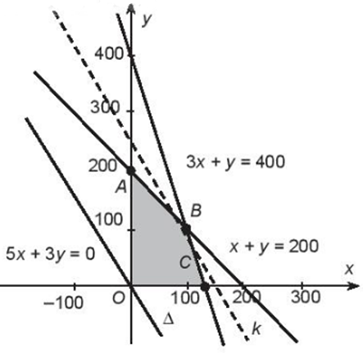
Nếu bán hết thì lợi nhuận lớp Việt có được là: d = 5x + 3y (nghìn đồng).
Để tìm lợi nhuận lớn nhất ta cần tìm giá trị lớn nhất của biểu thức:
d = 5x + 3y.
Khi đó các cặp (x; y) thoả mãn đề bài là các cặp số tự nhiên sao cho điểm M(x; y) nằm trong miền tứ giác OABC.
Ta có với Δ là đường thẳng có phương trình 5x + 3y = 0.
Gọi k là đường thẳng qua M và song song với Δ. Khi đó ta có d(M, Δ) = d(k, Δ). Do đó d lớn nhất tương ứng với khoảng cách giữa k và Δ lớn nhất. Từ hình vẽ ta có khoảng cách giữa k và Δ lớn nhất khi M trùng B. Do đó giá trị lớn nhất của d là
Vậy lợi nhuận tối đa mà lớp Việt có thể đạt được là 800 nghìn đồng khi các bạn mua và bán được 100 chiếc bánh mì và 100 chai nước.
Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 19: Phương trình đường thẳng
Bài 21: Đường tròn trong mặt phẳng tọa độ
Bài 22: Ba đường conic
Bài tập cuối chương 7