Giải bài tập Toán lớp 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách
A. Câu hỏi
Hoạt động 1 trang 36 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho hai đường thẳng
∆1: x – 2y + 3 = 0
∆2: 3x – y – 1 = 0
a) Điểm M(1; 2) có thuộc hai đường thẳng nói trên hay không?
b) Giải hệ ![]()
c) Chỉ ra mối quan hệ giữa toạ độ giao điểm của ∆1 và ∆2 với nghiệm của hệ phương trình trên.
Lời giải:
a) Thay toạ độ điểm M(1; 2) vào phương trình đường thẳng ∆1: x – 2y + 3 = 0 ta được 1 – 2.2 + 3 = 0 là mệnh đề đúng nên điểm M thuộc đường thẳng ∆1.
Thay toạ độ điểm M(1; 2) vào phương trình đường thẳng ∆2: 3x – y – 1 = 0 ta được 3.1 – 2 – 1= 0 là mệnh đề đúng nên điểm M thuộc đường thẳng ∆2.
Vậy M(1; 2) thuộc đường thẳng ∆1 và ∆2 hay M(1; 2) là giao điểm của hai đường thẳng ∆1; ∆2.
b) Xét hệ phương trình: ⇔
Trừ phương trình (1) cho phương trình (2) vế theo vế ta được:
– 5y + 10 = 0
⇔ 5y = 10
⇔ y = 10 : 5 = 2
Thay y = 2 vào phương trình x – 2y + 3 = 0 ta được: x – 2.2 + 3 = 0
⇔ x – 4 + 3 = 0
⇔ x – 1 = 0
⇔ x = 1
Vậy nghiệm của hệ phương trình là (2; 1).
c) Toạ độ giao điểm của ∆1 và ∆2 là nghiệm của hệ phương trình ![]()
Luyện tập 1 trang 37 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau:
a) ∆1: x + 4y – 3 = 0 và ∆2: x – 4y – 3 = 0;
b) ∆1: x + 2y – = 0 và ∆2: 2x + 4y – 3 = 0.
Lời giải:
a) Đường thẳng ∆1 có vectơ pháp tuyến (1; 4).
Đường thẳng ∆2 có vectơ pháp tuyến (1; -4).
Vì nullnên và là hai vectơ không cùng phương, do đó: ∆1 và ∆2 cắt nhau.
b) Đường thẳng ∆1 có vectơ pháp tuyến (1; 2)
Đường thẳng ∆2 có vectơ pháp tuyến (2; 4)
Vì = 2 nên ; là hai vectơ cùng phương nên ∆1 và ∆2 song song hoặc trùng nhau
Mặt khác, thay điểm A(; 0) vào phương trình đường thẳng ∆1 ta có: + 2.0 –= 0, do đó: điểm A(; 0) thuộc đường thẳng ∆1.
Thay điểm A(; 0) vào phương trình đường thẳng ∆2 ta có: 2 + 4.0 – 3= –≠ 0, do đó: điểm A(; 0) không thuộc đường thẳng ∆2.
Vậy ∆1 và ∆2 là hai đường thẳng song song.
Hoạt động 2 trang 37 Toán 10 Tập 2: Hai đường thẳng ∆1 và ∆2 cắt nhau tạo thành bốn góc (H.7.6). Các số đo của bốn góc đó có mỗi quan hệ gì với nhau?
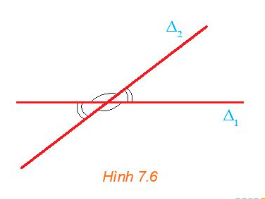
Lời giải:
Hai đường thẳng ∆1 và ∆2 cắt nhau tại điểm A và tạo thành bốn góc lần lượt là như hình vẽ:
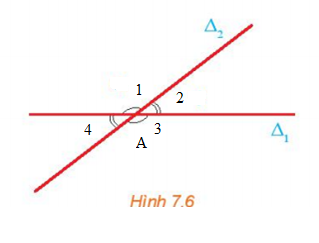
Ta thấy:
+) và , và là các cặp góc đối đỉnh.
⇒ = , =
+) + = 180° (hai góc kề bù)
+ = 180° (hai góc kề bù)
+ = 180° (hai góc kề bù)
+ = 180° (hai góc kề bù)
Hoạt động 3 trang 38 Toán 10 Tập 2: Cho hai đường thẳng cắt nhau ∆1 và ∆2 tương ứng có các vectơ pháp tuyến . Gọi φ là góc giữa hai đường thẳng đó (H7.7). Nêu mối quan hệ giữa:
a) góc φ và góc ();
b) cos φ và cos().
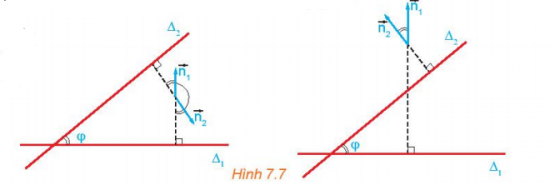
Lời giải:
a)
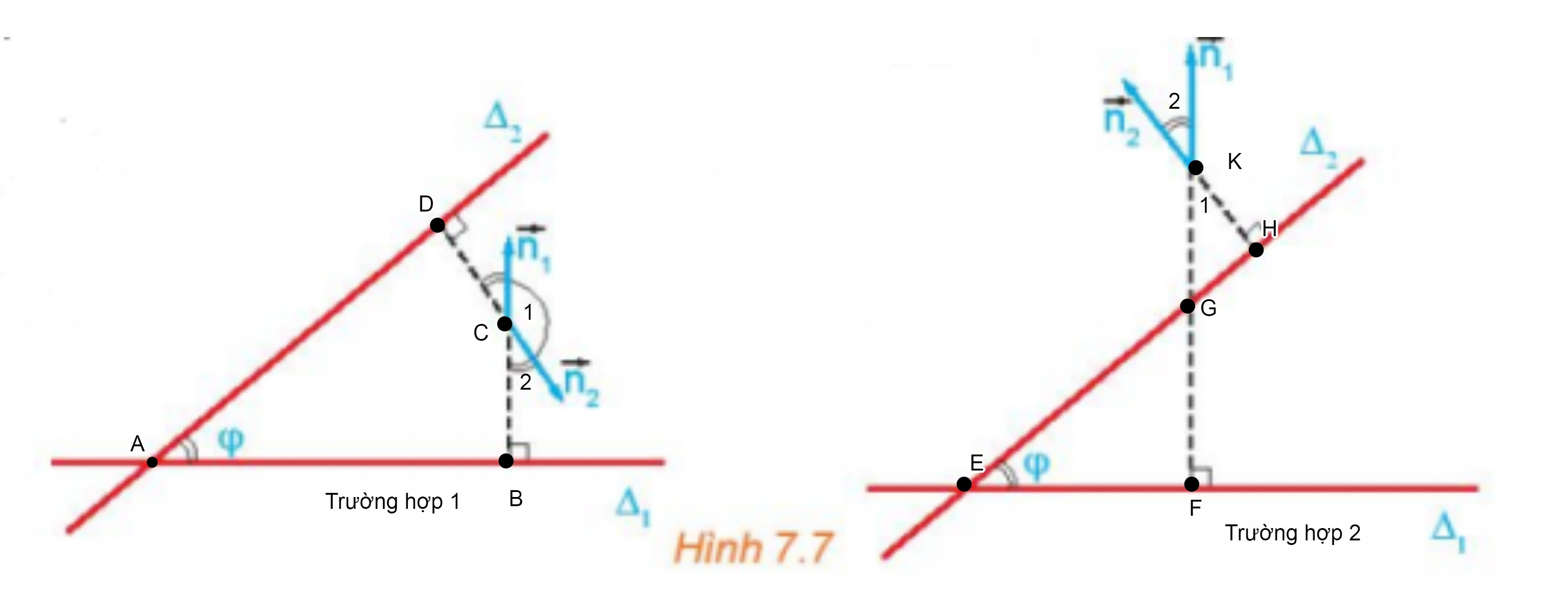
* Xét trường hợp 1:
Xét tứ giác ABCD có hai góc bằng 900 nên tứ giác ABCD là tứ giác nội tiếp.
Theo tính chất góc ngoài của tứ giác nội tiếp ta có : = φ
Mặt khác ta có: và là hai góc kề bù nên = 180°– = 180° – φ hay + φ = 180°
⇒ và φ là hai góc bù nhau. (1)
* Xét trường hợp 2:
Chứng minh tương tự ta có tứ giác EFHK là tứ giác nội tiếp
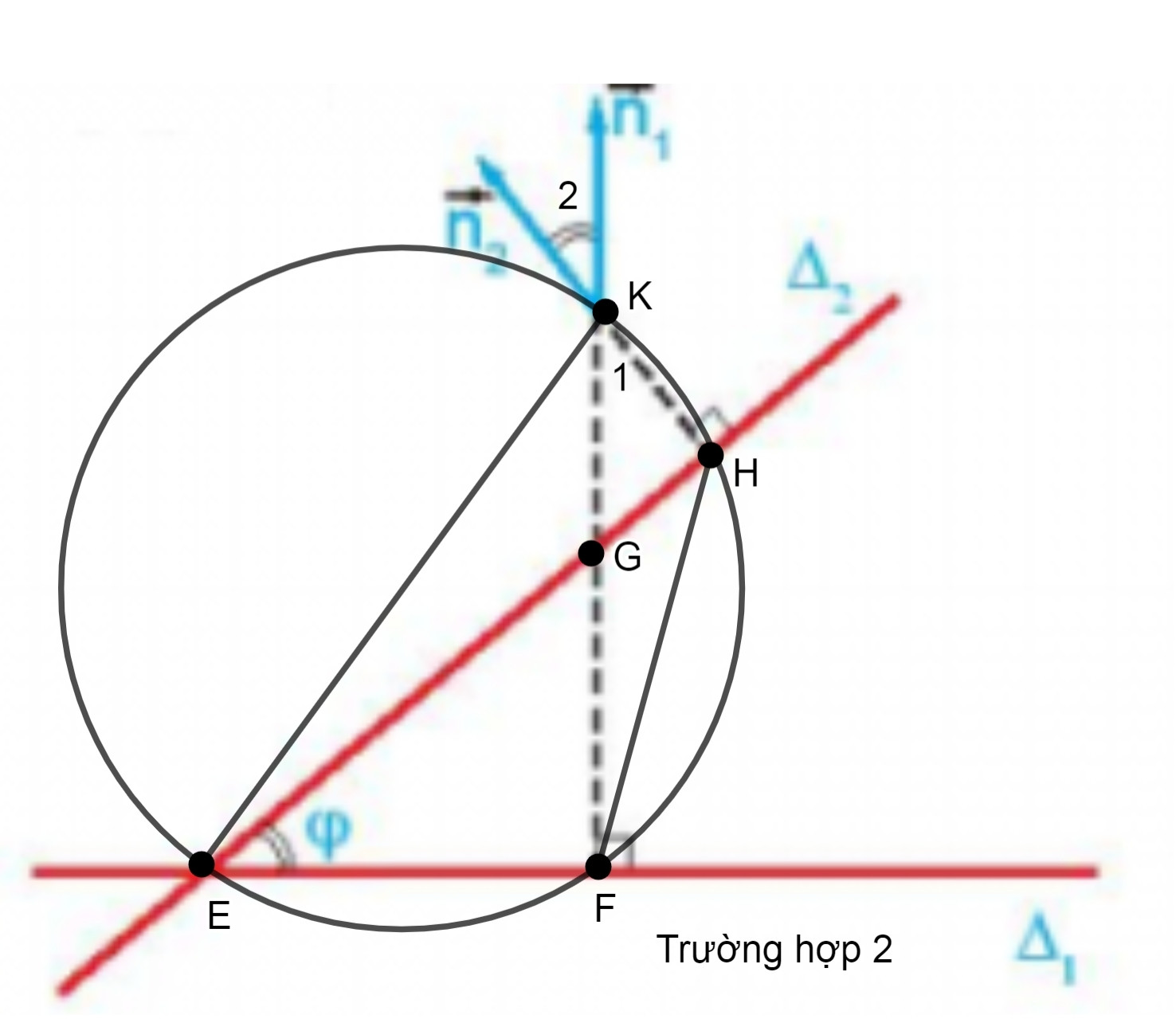
Ta có: = = φ (Vì hai góc nội tiếp và cùng chắn cung FH)
Mặt khác ta có: và là hai góc đối đỉnh nên =
⇒ = φ. (2)
Từ (1) và (2) suy ra: = φ hoặc + φ = 180°.
Vậy mối quan hệ giữa góc và góc φ là = φ hoặc + φ = 180°.
b)
* Xét trường hợp 1: = 180° – φ
Do đó cos= cos(180° – φ) = -cos φ
* Xét trường hợp 2 : = φ
Ta có: cos = cosφ.
Vậy cos = |cosφ|.
Luyện tập 2 trang 39 Toán 10 Tập 2: Tính góc giữa hai đường thẳng ∆1: x + 3y + 2 = 0 và 2: y = 3x + 1
Lời giải:
Phương trình đường thẳng ∆2 là y = 3x + 1 ⇔ 3x – y + 1 = 0
Đường thẳng ∆1 có vectơ pháp tuyến (1; 3)
Đường thẳng ∆2 có vectơ pháp tuyến (3; -1)
Gọi φ là góc giữa hai đường thẳng ∆1 và ∆2. Ta có:
cos φ = = = = 0.
⇒ = 90°.
Vậy góc giữa hai đường thẳng ∆1 và ∆2 là φ = 90°.
Luyện tập 3 trang 39 Toán 10 Tập 2: Tính góc giữa hai đường thẳng ∆1: và ∆2:.
Lời giải:
Đường thẳng ∆1 có vectơ chỉ phương là (1; -2) nên có vectơ pháp tuyến (2; 1)
Đường thẳng ∆2 có vectơ chỉ phương là (1; 3) nên có vectơ pháp tuyến (-3; 1)
Gọi φ là góc giữa hai đường thẳng ∆1 và ∆2. Ta có:
cos φ = = = = =.
⇒ φ = 45°.
Vậy góc giữa hai đường thẳng 1 và ∆2 là φ = 45°.
Luyện tập 4 trang 39 Toán 10 Tập 2: Cho đường thẳng ∆: y = ax + b với a ≠ 0.
a) Chứng minh rằng ∆ cắt trục hoành.
b) Lập phương trình đường thẳng ∆0 đi qua điểm O(0; 0) và song song (hoặc trùng) với ∆.
c) Hãy chỉ ra mối quan hệ giữa và
d) Gọi M là giao điểm của ∆0 với nửa đường tròn đơn vị và x0 là hoành độ của M. Tính tung độ của M theo x0 và a. Từ đó, chứng minh tan= a
Lời giải:
a) Phương trình đường thẳng ∆ có dạng ax – y + b = 0
Đường thẳng ∆ có vectơ pháp tuyến (a; -1) với a ≠ 0
Trục Ox có vectơ pháp tuyến là vectơ đơn vị (0; 1)
Ta có: a.1 – (-1).0 = a ≠ 0 nên và không cùng phương nên đường thẳng ∆ cắt trục hoành.
b) Vì đường thẳng ∆0 song song (hoặc trùng) với ∆ nên và cùng phương với nhau. Do đó chọn (a; -1).
Phương trình đường thẳng ∆0 đi qua điểm O(0; 0) và song song (hoặc trùng) với ∆ là:
a(x – 0) – 1(y – 0) = 0 hay ax – y = 0.
c) Do ∆0 song song với đường thẳng ∆ nên = (hai góc đồng vị).
Vậy = .
d) Vì M là giao điểm của ∆0 với nửa đường tròn đơn vị nên toạ độ điểm M thoả mãn phương trình đường thẳng ∆0
Do đó, ta có: ax0 – y = 0 ⇒ y = ax0
⇒ M(x0; ax0)
Mặt khác ta có: tan= tan= = a.
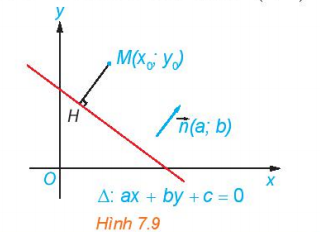
Hoạt động 4 trang 40 Toán 10 Tập 2: Cho điểm M(x0; y0) và đường thẳng ∆ : ax + by + c = 0 có vectơ pháp tuyến (a; b). Gọi H là hình chiếu vuông góc của M lên ∆ (H.7.9).
a) Chứng minh rằng
b) Gỉa sử H có toạ độ (x1; y1). Chứng minh rằng:
c) Chứng minh rằng HM =
Lời giải:
a) Ta có: = =
Mà và là hai vectơ cùng phương (vì cùng vuông góc với ∆) nên = 00
Do đó, = = .
Vậy (*) (đpcm)
b) Ta có: = ( x0 – x1; y0 – y1)
Mặt khác, ta có: = a.(x0 – x1) + b.(y0 – y1)
= ax0 – ax1 + by0 – by1
= ax0 + by0 – ax1– by1 (1)
Thoe giả thiết ta có điểm H thuộc đường thẳng ∆ nên ax1 + by1 + c = 0
⇒ – ax1 – by1 = c (2)
Thay (2) và (1) ta được: = a.(x0 – x1) + b.(y0 – y1) = ax0 + by0 + c (đpcm)
Hay (**)
c) Từ (*) và (**) ta có: = ( = ).
⇒ MH = (đpcm).
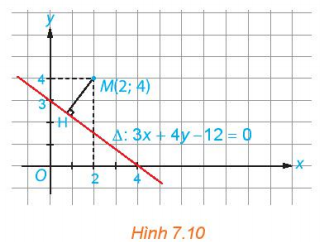
Trải nghiệm trang 40 Toán 10 Tập 2: Đo trực tiếp khoảng cách từ điểm M đến đường thẳng ∆ (H.7.10) và giải thích vì sao kết quả đo đạc đó phù hợp với kết quả tính toán trong lời giải của Ví dụ 4.
Lời giải:
Đo trực tiếp khoảng cách từ điểm M đến đường thẳng ∆ là MH = 2 (đơn vị độ dài).
Kết quả đo đạc đó phù hợp với kết quả tính toán trong lời giải của Ví dụ 4 vì ở cả Ví dụ 4 và bài trải nghiệm thì đều tính khoảng cách từ điểm M (2; 4) đến đường thẳng ∆: 3x + 4y – 12 = 0.
Luyện tập 5 trang 40 Toán 10 Tập 2: Tính khoảng cách từ điểm M(1; 2) đến đường thẳng ∆:
Lời giải:
Đường thẳng ∆ có vectơ chỉ phương (3; -4). Do đó, vectơ pháp tuyến của ∆ là: (4; 3).
Lấy điểm A(5; -5) thuộc ∆.
Ta có phương trình tổng quát của đường thẳng ∆ là:
4(x – 5) + 3(y + 5) = 0
⇔ 4x – 20 + 3y + 15 = 0 hay 4x + 3y – 5 = 0
Khi đó khoảng cách từ điểm M(1; 2) đến đường thẳng ∆ là :
d(M; ∆) = = = 1.
Vậy khoảng cách từ điểm M đến đường thẳng ∆ là 1.
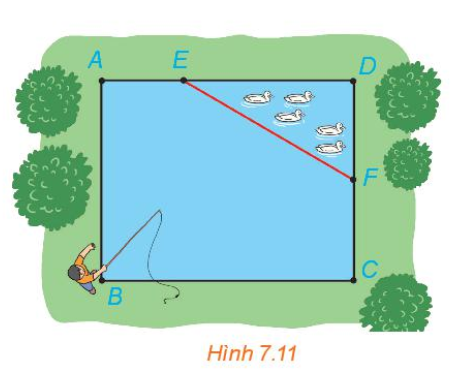
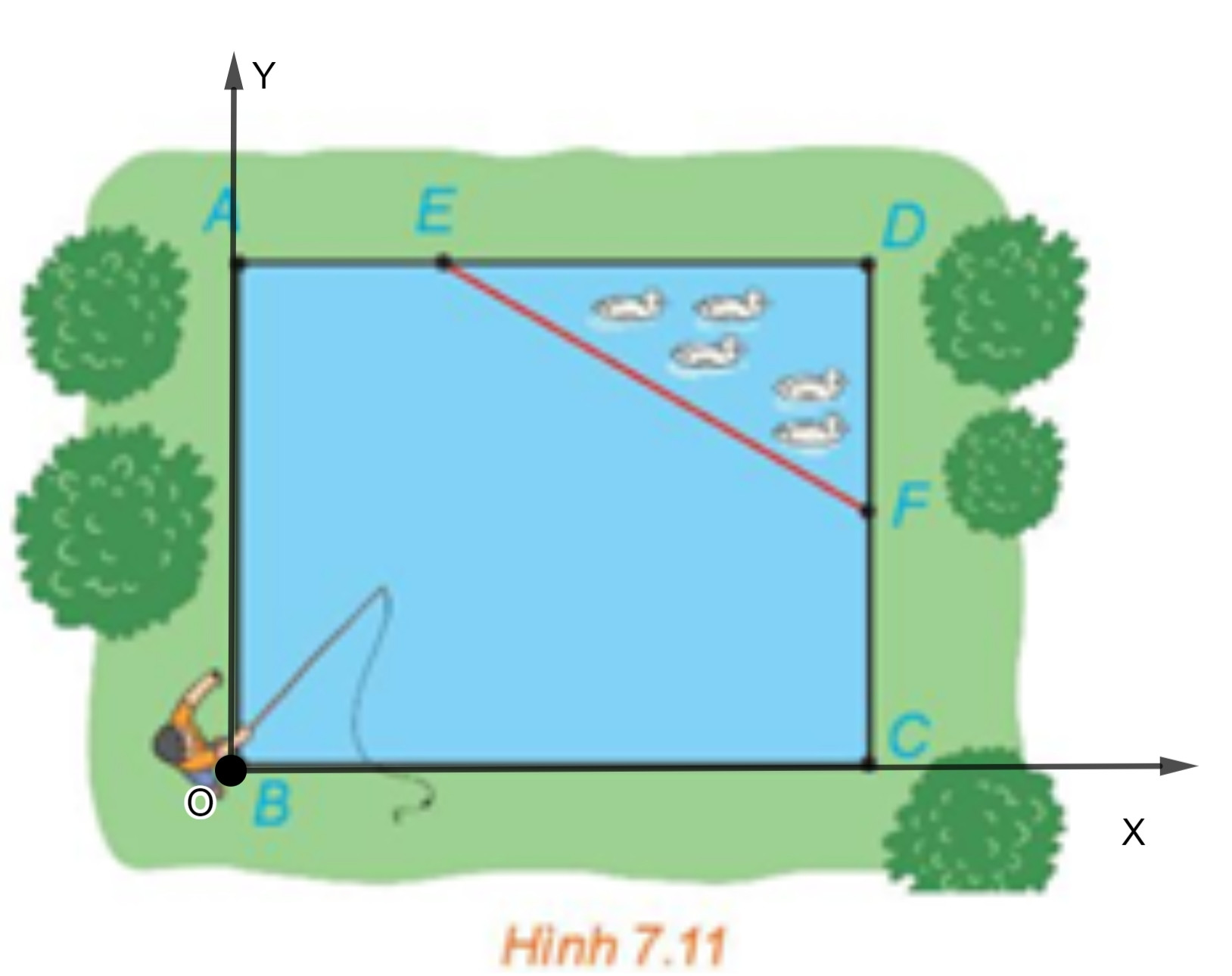
Vận dụng trang 41 Toán 10 Tập 2: Nhân dịp nghỉ hè, Nam về quê ở với ông bà nội. Nhà ông bà nội có một ao cá có dạng hình chữ nhật ABCD với chiều dài AD = 15m, chiều rộng AB = 12m. Phần tam giác DEF là nơi ông bà nuôi vịt, AE = 5m, CF = 6m (H.7.11)
a) Chọn hệ trục toạ độ Oxy, có điểm O trùng với điểm B, các tia Ox, Oy tương ứng trùng với các tia BC, BA. Chọn 1 đơn vị độ dài trên mặt phẳng toạ độ tương ứng 1m trong thực tế. Hãy xác định toạ độ của các điểm A, B, C, D, E, F và viết phương trình đường thẳng EF.
b) Nam đứng ở vị trí B câu cá có thể quăng lưỡi câu xa 10,7 m . Hỏi lưỡi câu có thể rơi vào ao nuôi vịt hay không ?
Lời giải:
a) Đặt hệ trục tọa độ như hình vẽ:
Vì ABCD là hình chữ nhật nên ta có: AD = BC = 15m, AB = DC = 12m, AE = 5m, CF = 6m.
Khi đó, toạ các điểm lần lượt là: C(15; 0), A(0; 12), E(5; 12), D(15; 12), F(15; 6), B(0; 0).
Ta có: = (10; -6)
Đường thẳng EF đi qua điểm E(5; 12) và nhận = = (5, -3) làm vectơ chỉ phương do đó vectơ pháp tuyến của đường thẳng EF là: (3; 5)
Suy ra phương trình tổng quát của đường thẳng EF là: 3(x – 5) + 5(y – 12) = 0 hay 3x + 5y – 75 = 0.
Vậy phương trình tổng quát của đường thẳng EF là 3x + 5y – 75 = 0.
b) Khoảng cách từ điểm B đến đường thẳng EF là:
d(B, EF) = = ≈ 12,86 > 10,7
Vậy nếu Nam đứng ở vị trí B câu cá thì lưỡi câu không thể rơi vào ao nuôi vịt.
B. Bài tập
Bài 7.7 trang 41 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau:
a) ∆1 : 3x + y –= 0 và ∆2 : 6x + 2y –= 0
b) d1 : x –y + 2 = 0 và d2 : x – 3y + 2 = 0
c) m1 : x – 2y + 1= 0 và m2 : 3x + y – 2 = 0
Lời giải:
a) Vì 3x + y –= 0 ⇔ . (3x + y –) = 0
⇔ 6x + 2y –= 0
Vậy ∆1 và ∆2 trùng nhau.
b)
Đường thẳng d1 có vectơ pháp tuyến (1; )
Đường thẳng d2 có vectơ pháp tuyến (; -3)
Vì =nên ; là hai vectơ cùng phương nên d1 và d2 song song hoặc trùng nhau.
Mặt khác, thay điểm A(–2; 0) vào phương trình đường thẳng d1, ta có: –2 + .0 + 2 = 0, do đó: điểm A(–2; 0)thuộc đường thẳng d1.
Thay điểm A(–2; 0) vào phương trình đường thẳng d2 , ta có:
.(–2) – 3.0 + 2 = –2+ 2 ≠ 0, do đó điểm A(–2; 0) không thuộc đường thẳng d2 .
Vậy d1 và d2 là hai đường thẳng song song
c)
Đường thẳng m1 có vectơ pháp tuyến (1; -2)
Đường thẳng m2 có vectơ pháp tuyến (3; 1)
Vì nên và là hai vectơ không cùng phương , do đó: m1 và m2 cắt nhau
Bài 7.8 trang 41 Toán 10 Tập 2: Tính góc giữa các cặp đường thẳng sau:
a) ∆1 : x + y – 4 = 0 và ∆2 : x +y + 3 = 0
b) d1 : và d2 : (t; s là các tham số)
Lời giải:
a) Đường thẳng ∆1 có vectơ pháp tuyến (; 1)
Đường thẳng ∆2 có vectơ pháp tuyến (1; )
Gọi α là góc giữa hai đường thẳng ∆1 và ∆2. Ta có:
cos α = == =
Vậy góc giữa hai đường thẳng ∆1 và ∆2 là α = 30°.
b)
Đường thẳng d1 có vectơ chỉ phương (2; 4) do đó: vectơ pháp tuyến (4; -2)
Đường thẳng d2 có vectơ chỉ phương (1; -3) do đó: vectơ pháp tuyến (3; 1)
Gọi β là góc giữa hai đường thẳng d1 và d2. Ta có:
cos β = == =
Vậy góc giữa hai đường thẳng ∆1 và ∆2 là β = 45°.
Bài 7.9 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ Oxy cho điểm A(0; –2) và đường thẳng ∆ : x + y – 4 = 0
a) Tính khoảng cách từ điểm A đến đường thẳng ∆.
b) Viết phương trình đường thẳng a đi qua điểm M(–1; 0) và song song với ∆.
c) Viết phương trình đường thẳng b đi qua điểm N(0; 3) và vuông góc với ∆.
Lời giải:
a) Đường thẳng ∆ có vectơ pháp tuyến (1; 1)
d(A; ∆) = = = .
Vậy khoảng cách từ điểm A đến đường thẳng ∆ là d(A; ∆) = .
b) Đường thẳng a song song với đường thẳng ∆ nên phương trình đường thẳng a có dạng: x + y + c = 0
Vì đường thẳng a đi qua điểm M(–1; 0) nên -1 + 0 + c = 0 ⇒ c = 1
Vậy phương trình đường thẳng a là: x + y + 1 = 0.
c) Đường thẳng b vuông góc với đường thẳng ∆ nên đường thẳng b nhận vectơ chỉ phương của đường thẳng ∆ làm vectơ pháp tuyến
Ta có đường thẳng ∆ có VTCP là: (1; –1) nên VTPT của đường thẳng ∆ là (1; –1).
Vậy phương trình đường thẳng b là: 1.(x – 0) – 1(y – 3) = 0 hay x – y + 3 = 0.
Bài 7.10 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho tam giác ABC có A(1; 0), B(3; 2) và C(–2; –1)
a) Tính độ dài đường cao kẻ từ đỉnh A của tam giác ABC.
b) Tính diện tích ABC.
Lời giải:
a) Ta có: = (5; 3)
Đường thẳng BC có là vectơ chỉ phương , do đó: vectơ pháp tuyến của đường thẳng BC là (3; –5)
Phương trình đường thẳng BC là: 3(x – 3) – 5(y – 2) = 0 hay 3x – 5y + 1 = 0
Độ dài đường cao kẻ từ đỉnh A của tam giác ABC là khoảng cách từ điểm A đến đường thẳng BC
AH = d(A; BC) = = = .
Vậy độ dài đường cao kẻ từ đỉnh A của tam giác ABC là (đvđd) .
b) BC = =
Vậy diện tích tam giác ABC là: S = = = 2 (đvdt).
Bài 7.11 trang 42 Toán 10 Tập 2: Chứng minh hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) vuông góc với nhau khi và chỉ khi aa’ = –1
Lời giải:
* Giả sử d vuông góc d’, ta cần chứng minh aa’ = –1
Đường thẳng d có vectơ pháp tuyến (a; –1)
Đường thẳng d’ có vectơ pháp tuyến (a’; –1)
Vì d vuông góc d’ nên .= 0
⇒ aa’ + (–1).( –1) = 0
⇔ aa’ + 1 = 0 hay aa’ = –1 (đpcm)
* Giả sử hai đường thẳng d và d’ có aa’ = –1, ta cần chứng minh d vuông góc d’
Xét tích vô hướng .= aa’ + (–1).( –1) = aa’ + 1
Mà aa’ = –1 nên .= (–1) + 1 = 0
⇒ ⊥hay d ⊥ d’ (đpcm)
Bài 7.12 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín hiệu đặt tại 3 vị trí O(0; 0), A(1; 0), B(1; 3) nhận được cùng một thời điểm. Hãy xác định vị trí phát tín hiệu âm thanh.
Lời giải:
Gọi vị trí phát tín hiệu âm thanh là H (x; y)
Ta có:
= (x; y) ⇒ OH =
= (x – 1; y) ⇒ AH =
= (x – 1; y – 3) ⇒ BH =
Vì tín hiệu nhận được tại 3 vị trí cùng 1 thời điểm nên OH = AH = BH
Từ đó ta có hệ phương trình:
⇔
⇒
⇔
⇔
⇒
Vậy điểm cần tìm là H
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 19: Phương trình đường thẳng
Bài 21: Đường tròn trong mặt phẳng tọa độ
Bài 22: Ba đường Conic
Bài tập cuối chương 7